[知识点] 7.1 栈,队列与链表
总目录 > 7 数据结构 > 7.1 栈,队列与链表
前言
马上要考数据结构了,停更一个星期后决定先把数据结构这一块复习一遍。
子目录列表
1、数据结构简介
2、栈
3、队列
4、链表
7.1 栈,队列与链表
1、数据结构简介
数据结构,顾名思义,计算机存储数据的结构。最简单的,变量,数组,都是数据结构。一般情况下对于数据结构的学习中,这些就直接略过而归入语言基础了,而数据结构专题往往从栈,队列与链表这三大基本结构开始介绍。
程序的运行离不开数据结构,而不同的数据结构各有优劣,对于不同的问题,选取合适的数据结构能够大幅提升算法的效率。
2、栈
① 概念
栈(stack)是最常见的线性数据结构之一,并且栈这个概念在计算机中经常被提及——汇编语言里有堆栈操作程序,平常编程时会提到栈溢出……
那么栈到底是什么?从中文里似乎不能直接想到,那么从英文入手 —— stack,其本义为堆叠(n. & v.),想象一下,新学期开学了,学校下发了 3 本新教材,你想把它们整理好并堆成一叠放在寝室——先把数据结构放在桌上,再把汇编语言放在数据结构上面,再把计算机组成放在汇编语言上面,叠好了。这个过程是从下到上堆叠的。而现在开始上数据结构课了,如果你需要从里面取出教材,在不考虑直接从下面抽取的情况,则必须要从最上方的计算机组成开始取,然后再拿出汇编语言,最后才能拿到数据结构。
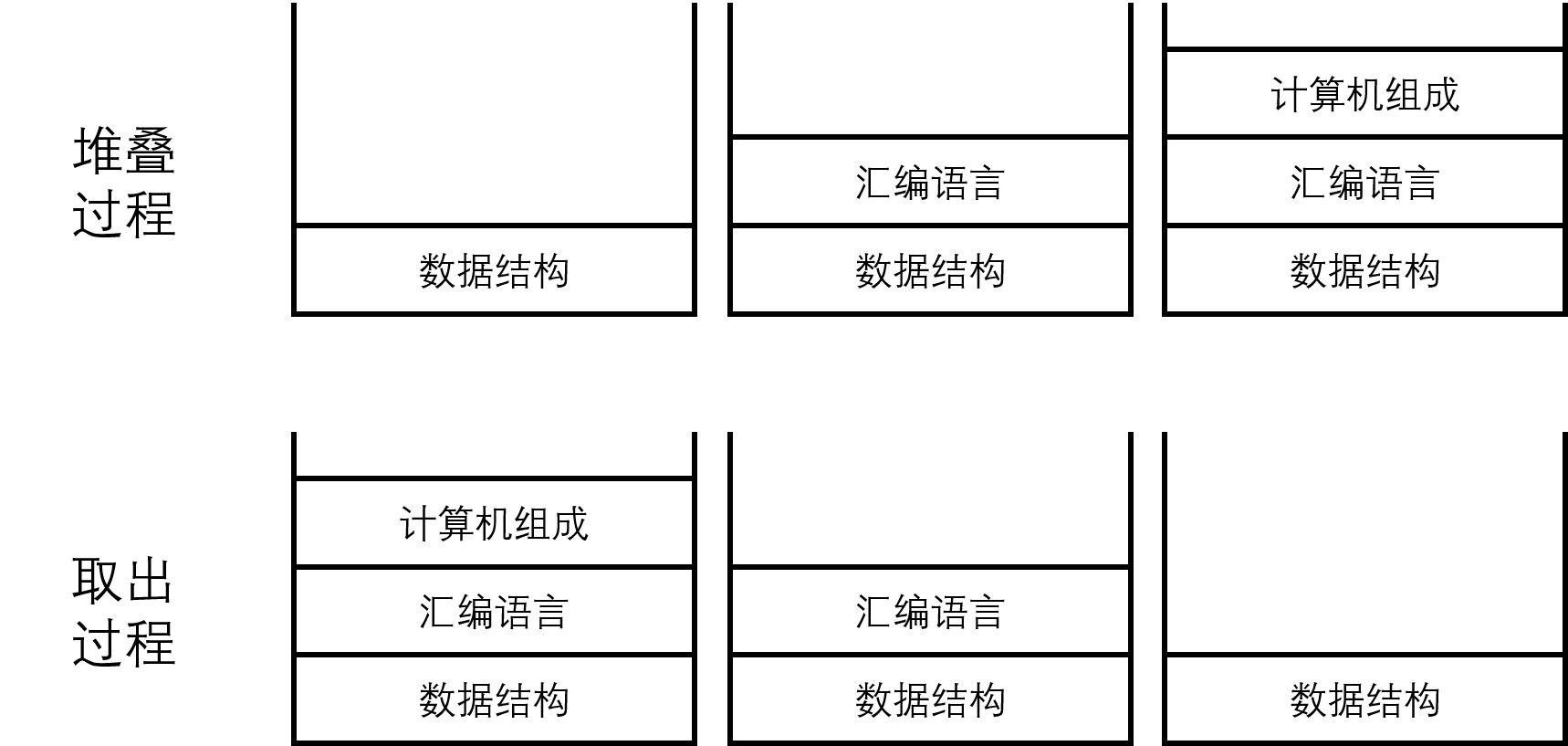
这种结构的最大特点是——后加入的数据必须最先取出,简称为后进先出(LIFO, last in first out)。
我们将栈的最上方称为栈顶,最下方称为栈底,每次加入或弹出数据都只能从栈顶进行。
汉诺塔问题也是个比较典型的栈——每次在堆叠的时候,我们必须将最上方那块最小的先移动到其他位置,才能移动下方的,以此类推——而上次介绍汉诺塔问题是在递归部分(请参见:2.2 递归与分治)。
说到递归,我们发现它似乎和栈有异曲同工之妙——递归过程不也是对于最后进入的层必须最先处理吗?没错,递归其实本质也是栈结构,这就是为什么在介绍 DFS 的时候提到,DFS 是通过栈这个数据结构实现的(请参见:3.1 DFS / BFS 搜索)
汇编语言里提到的堆栈操作程序同理,将寄存器中的数据 PUSH 进去,最先 POP 出来的则是最后 PUSH 进去的。
② 常用操作
那么对于这样一个数据结构,可以进行哪些操作?我们还是模拟一下取书的过程:
> 首先肯定可以把书放入;
> 然后可以看到最上方的书是什么(下方的书不能看到);
> 然后可以取出最上方的书;
> 可以对书本数量进行计数;
> 可以判断是否还有书。
那么这五个过程,可以分别对应栈的五种操作:
> push:将元素加入栈顶;
> top:获取栈顶元素;
> pop:将栈顶元素取出;
> size:获取栈内元素个数;
> empty:判断栈是否为空。
③ 代码实现
先给出一段手搓的栈的实现代码。
1 #include <bits/stdc++.h> 2 using namespace std; 3 4 #define MAXN 1005 5 6 class Stack { 7 int stk[MAXN], tot; 8 public: 9 Stack() : tot(0) {} 10 void push(int o) { 11 tot++, stk[tot] = o; 12 } 13 int top() { 14 return stk[tot]; 15 } 16 void pop() { 17 tot--; 18 } 19 int size() { 20 return tot; 21 } 22 bool empty() { 23 return tot; 24 } 25 }; 26 27 int main() { 28 Stack s; 29 s.push(1), s.push(2), s.push(3); 30 cout << s.size() << ' ' << s.top() << endl; 31 s.pop(), s.pop(); 32 cout << s.size() << ' ' << s.top() << endl; 33 s.pop(); 34 cout << s.empty(); 35 return 0; 36 }
五个操作应该都不用过多解释。
如果使用的是 C++,那么学过 STL(请参见:1.3.1 STL 简介)应该就知道,可以使用 STL 中的 stack 来实现栈,其构造方式为:
stack <Typename T, Container> s;
其中 T 表示数据类型,除了 int, double 等基本类型之外,同样支持诸如类等更高级的类型。Container 为容器,可省略,省略则默认为 deque,同时标准容器 vector, list 也可以使用。关于容器的使用,暂时不介绍。
STL 内的栈支持的五种方法同上,也就是说将上述代码主程序创建的栈从手工栈改成 STL 栈,对结果没有影响。感兴趣的可以去 <stack> 库看看实现方式。
④ 应用举例
栈的应用和递归思想的应用基本是一致的,因为递归思想本身就是通过栈实现。常提的几种题型包括:
(1) 进制转换
(2) 括号匹配
(3) 行编辑程序问题
(4) 表达式求值
(5) 汉诺塔问题
等等。
2、队列
① 概念
和栈通常一起提及的另一种数据结构——队列(queue),这个概念就很好理解了,因为生活中随处可见排队的现象,对于一列排队买包子的人,必然是先开始排队的先买到包子,则和栈结构恰好相反,队列结构的最大特点是——先加入的数据最先取出,简称为先进先出(FIFO, first in first out)。
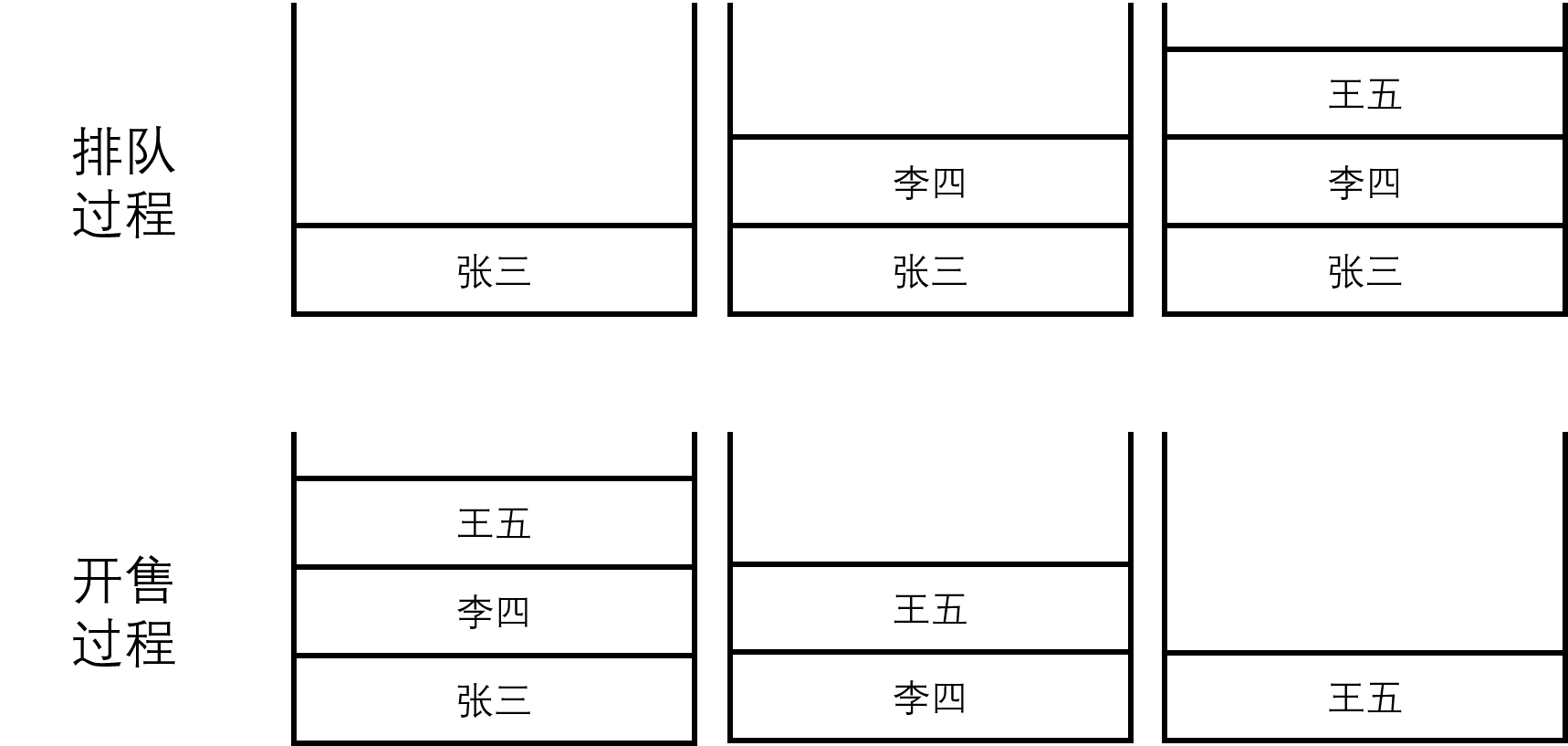
我们将队列的最前方称为队首,最尾端称为队尾,每次加入数据都只能从队尾加入,而每次弹出数据只能从队首弹出。
② 常用操作
对于队列,可以进行的操作和栈类似:
> push:将元素加入队尾;
> front:获取队首元素;
> back:获取队尾元素;
> pop:将队首元素取出;
> size:获取队列中元素个数;
> empty:判断队列是否为空。
③ 代码实现
由于栈只需要对栈顶元素进行操作,所以只需要一个变量 size,就可以同时完成加入,访问,取出,获取元素,判断是否为空 5 种操作。队列则因为加入和弹出分别在队首和队尾,则需要两个变量 head 和 tail。
1 #include <bits/stdc++.h> 2 using namespace std; 3 4 #define MAXN 1005 5 6 class Queue { 7 int q[MAXN], head, tail; 8 public: 9 Queue() : head(1), tail(0) {} 10 void push(int o) { 11 tail++, q[tail] = o; 12 } 13 int back() { 14 return q[tail]; 15 } 16 int front() { 17 return q[head]; 18 } 19 void pop() { 20 head++; 21 } 22 int size() { 23 return tail - head + 1; 24 } 25 bool empty() { 26 return tail - head > 0; 27 } 28 }; 29 30 int main() { 31 Queue q; 32 q.push(1), q.push(2), q.push(3); 33 cout << q.size() << endl; 34 cout << q.front() << ' ' << q.back() << endl; 35 q.pop(), q.pop(); 36 cout << q.size() << endl; 37 q.pop(); 38 cout << q.empty(); 39 return 0; 40 }
上述代码将队列封装在一个类中了,目的是规范化,其实通常可以不用这样规矩,简单一点的框架伪代码可以为:
1 int head = 1, tail = 2; 2 while (head != tail) { 3 int o = q[head]; 4 for (...) { 5 if (...) 6 tail++, q[tail] = v; 7 } 8 head++; 9 }
同样地,如果使用的是 C++,可以使用 STL 队列。其构造方式为:
queue <Typename T, Container> q;
和 stack 一样,它们都是容器适配器,允许加入容器 Container。
STL 队列支持的六种方法同上。
④ 应用举例
DFS 是用栈实现的,而 BFS(请参见:3.1 DFS / BFS 搜索)是用队列实现的。在清晰认识到队列的原理后,对 BFS 的理解应该就轻松多了。
⑤ 其他队列
> 循环队列
在数据量较大的情况下,为了防止溢出,可以使队列首尾相连进行循环,即 x 的后继为 (x + 1) % size,但这样可能会覆盖有效数据。
> 双端队列
队首队尾均支持插入和弹出元素操作。
> 优先队列
请参见:7.4 堆与优先队列
3、链表
① 链表与数组
常见的数组,和上述的栈和队列,它们的共同特点是都属于线性结构,在数据结构中称之为线性表。除此之外,和数组类似的还有一种线性表——链表(linked-list)。
数组的数据是相互独立的,对于任意一个元素,它只和它在数组中的位置有对应关系,所以在访问数据时时间复杂度为 O(1),而插入、删除数据为 O(n),因为一个元素的增加或减少要影响接下来所有的元素。
链表则相反——它的结构类似于链子,元素本身没有固定的位置,而是靠元素和元素之间的位置关系来维持结构,下图体现了数组和链表的区别:
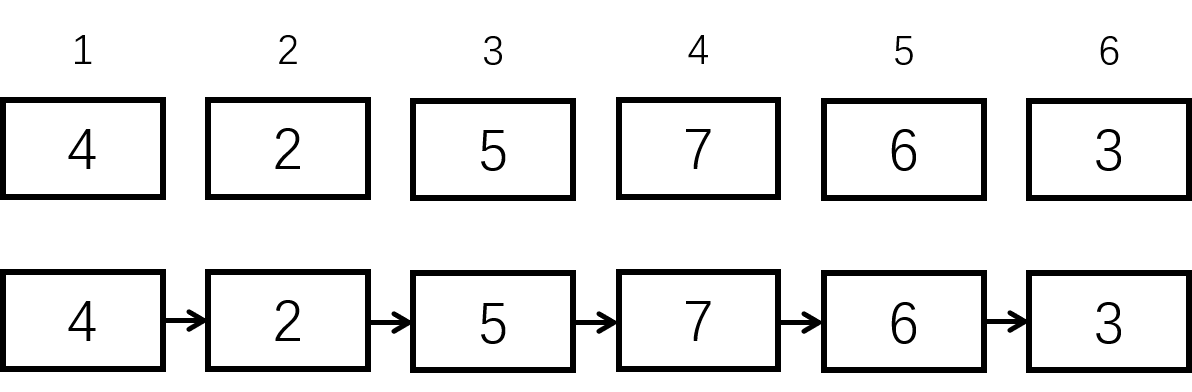
对于链表,访问数据时间复杂度为 O(n),插入、删除数据为 O(1)。上图展示的是单向链表,每个元素有一个后继指针,同时还有双向链表,即每个元素有前驱指针和后继指针两个。下面先介绍单向链表。
② 构建
class Node { int v; Node *nxt; };
这是采用指针形式的单向链表构建方式。Node 为结点,其包含两个数据成员:v 为该结点的值,*nxt 为其后继结点的指针,用以链接元素。当然也可以不使用指针而直接定义一个变量,但就需要更多的空间了。
③ 常用操作
相比栈和队列,链表可操作性更强,操作的具体流程也更为复杂。这里先列举最常规的操作:
> insert:在任意位置插入一个元素
给出一个具体位置(指针 p),直接实现 O(1) 插入,举例:

假设指针 p 指向 5,则表示在 5 后面插入元素。先建立一个新结点,将 9 存入该结点,再将 5 的后继指针赋值给 9 的后继指针,而后将 5 的后继指针指向 9,插入就完成了。这是从中间插入的过程,由于是插入到给定指针的元素后面,如果要在链表头插入数据,则需要特判,同时,要维护链表的头指针,如果从头插入,则头指针需要同时修改。
代码实现见下方。
> erase:删除任意位置的一个元素
单向链表的删除操作相对难理解一些。因为没有前驱指针,我们只能通过将被删除元素的后继元素覆盖到被删除的元素上,如图:
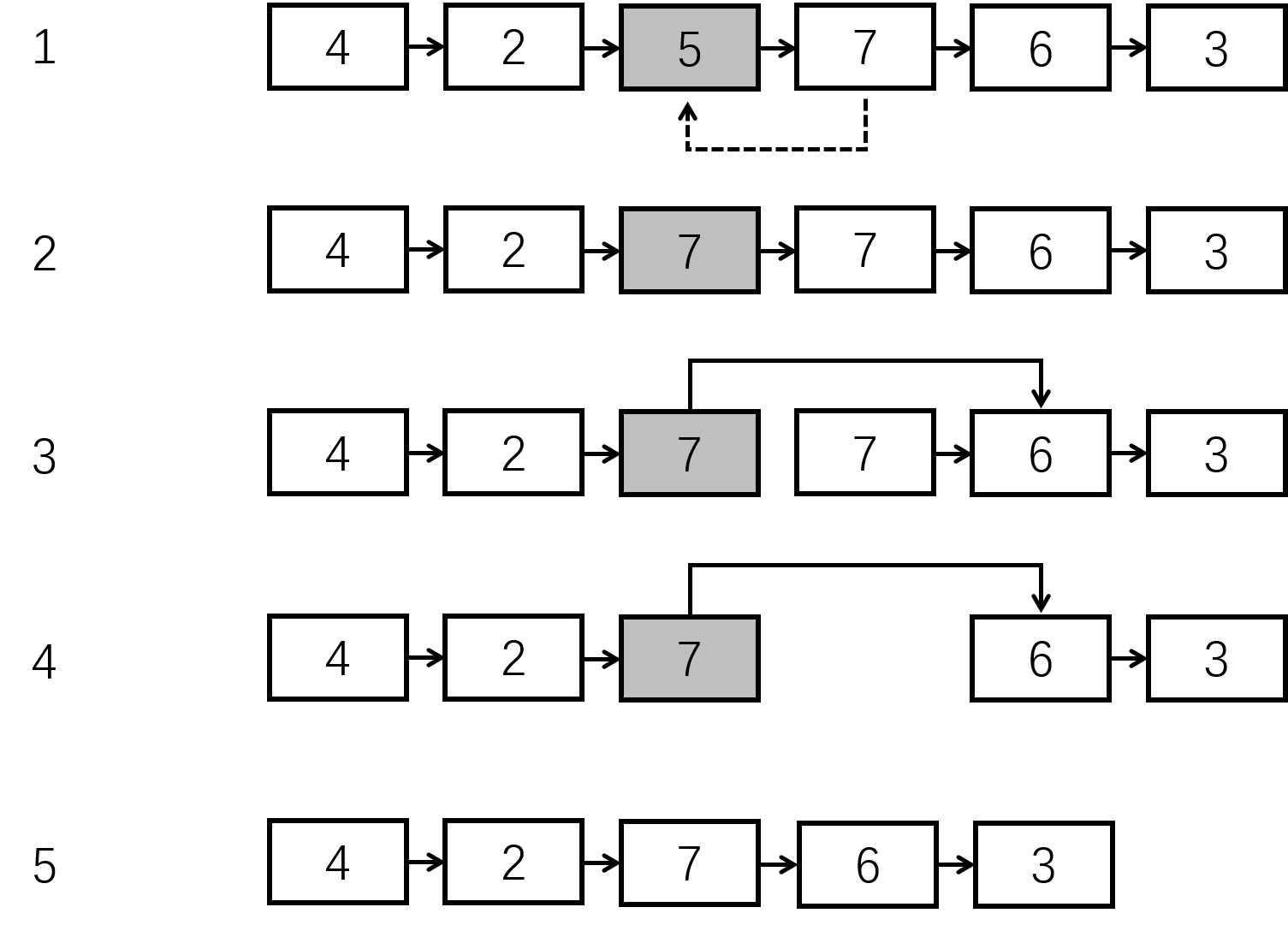
图中可以看出,虽然我们确实将 5 删除了,但其实是把 7 赋值到原来 5 所在的结点,再通过修改指针将 7 所在的那个结点删除了,通过这种方式间接删去了 5。
> size:获取链表内元素个数
> empty:判断链表是否为空
④ 代码实现
1 class List { 2 int tot; 3 Node *head; 4 public: 5 void insert(int o) { 6 Node *node = new Node; 7 node -> v = o; 8 node -> nxt = head; 9 head -> pre = node; 10 head = node; 11 tot++; 12 } 13 void insert(int o, Node *p) { 14 Node *node = new Node; 15 node -> v = o; 16 node -> nxt = p -> nxt; 17 node -> pre = p; 18 p -> nxt -> pre = node; 19 p -> nxt = node; 20 tot++; 21 } 22 void erase(Node *p) { 23 p -> pre -> nxt = p -> nxt; 24 p -> nxt -> pre = p -> pre; 25 delete p; 26 tot--; 27 } 28 int size() { 29 return tot; 30 } 31 bool empty() { 32 return tot; 33 } 34 };
⑤ 双向链表与 list
双向链表很好理解,新增加一个前驱指针后,可以进行反向遍历,对应的操作的具体实现会有所不同,比如删除操作就不再需要围魏救赵了。下面直接给出代码。
1 class List { 2 int tot; 3 Node *head; 4 public: 5 void insert(int o) { 6 Node *node = new Node; 7 node -> v = o; 8 node -> nxt = head; 9 head = node; 10 tot++; 11 } 12 void insert(int o, Node *p) { 13 Node *node = new Node; 14 node -> v = o; 15 node -> nxt = p -> nxt; 16 p -> nxt = node; 17 tot++; 18 } 19 void erase(Node *p) { 20 p -> v = p -> nxt -> v; 21 Node *node = p -> nxt; 22 p -> nxt = p -> nxt -> nxt; 23 tot--; 24 } 25 int size() { 26 return tot; 27 } 28 bool empty() { 29 return tot; 30 } 31 };
C++ 的 STL 中提供的是双向链表 list,功能相当丰富,提供的成员方法多达三十多种,除了上述几种操作之外,还有诸如:clear 清空链表,remove 删除特定值元素,sort 链表排序,unique 元素去重等等。
不同于 stack 和 queue 是容器适配器,list 就是容器,需要通过迭代器 iterator 访问元素,上面给出的单向和双向链表中其实都略过了查询操作,关于 STL 容器的介绍请参见:<施工中>,此处不深入解释。
⑤ 循环链表
链表同样可以循环,即链表头和链表尾相连。
⑥ 应用举例
> 图的存储结构之一——邻接链表,请参见:8.2 图的存储与遍历
> 解决哈希冲突的链地址法,请参见:7.2 哈希表




