[知识点] 3.2 四种改进搜索算法
总目录 > 3 搜索 > 3.2 四种改进搜索算法
前言
上一节介绍的是最基础的 DFS 和 BFS,适用范围很广,但是针对性不强,遇到一些模型比较特殊的,可能效率就不够高了。这里介绍的四种改进的搜索,在特定情况下会更优于普通的搜索。
子目录列表
1、双向搜索
2、折半搜索
3、迭代加深搜索
4、启发式搜索
3.2 四种改进搜索算法
1、双向搜索
从起点和终点同时开始进行搜索,以中间点相遇作为终止条件。只基于 BFS。
最开始同时将加入起点和终点加入队列,并做好标记,在开始搜索时先判断属于从起点开始的还是从终点开始的,然后和普通 BFS 一样进行扩展。如果当前结点为从起点(终点)开始的,而扩展的结点已经带有从终点(起点)开始的标记,则说明已经相遇,而该点即为中间点,即可终止搜索。
适用于从起点出发和进入终点的路段较为狭窄,而中间部分较为宽广的情况。
BFS 函数大致流程:
> 起点和终点加入队列的第 1 位和第 2 位,并分别标记为 1 和 2
> 当队列不空时,从队首扩展新的结点,如果
① 新结点的标记数和队首标记数不同,即一个 1 和一个 2,则说明搜索两端相遇,循环结束
② 队首标记数为 1,将新结点也标记为 1,加入队尾
③ 队首标记数为 2,将新结点也标记为 2,加入队尾
> 弹出队首
2、折半搜索
又称为 meet-in-middle 搜索。将整个搜索过程分成两半,分别进行搜索,最后将搜索结果合并。只基于 DFS。
看网上不少地方将其归为双向搜索,感觉还是有点区别的,双向搜索强调的是起点终点同时向中间靠拢,而折半搜索只是将过程分成两半——先把前半段按照正常的步骤搜索,并通过某种方式将已经得到的状态记录下来,并利用记录下来的状态继续搜索后半段。
适用于直接暴力 DFS 会导致超时,而指数减半后不会的情况。通常 n 是个较小的数。
之前似乎从没用过,看其他地方的一些例题时似乎还碰到了直接做过的题目,当时并不知道这种搜索方法。下面给出几个例题:
【USACO09】【灯】有 n 盏灯,每盏灯与若干盏灯相连,每盏灯上都有一个开关,如果按下一盏灯上的开关,这盏灯以及与之相连的所有灯的开关状态都会改变。一开始所有灯都是关着的,你需要将所有灯打开,求最小的按开关次数。(1 <= n <= 35)
思路:
最简单的暴力 DFS,枚举每盏灯的状态是开还是关,最后判断是否全部开了,求操作次数最小值,最大时间复杂度为 O(2 ^ 35),超时。
而使用折半 DFS,首先对前 n / 2 盏灯进行如上枚举,则时间复杂度为 O(2 ^ (n / 2));然后将所有状态记录下来,也只有 2 ^ (n / 2) 种;再对剩余一半的灯进行枚举,每次枚举后和前一轮已经记录的情况合并,看是否所有灯全部开了,并记录操作次数,其最小值即为答案。
具体实现的话涉及到的知识比较多:
① 关系图:灯的关系直接视作无向图,存储时可以用邻接链表(关于图的存储,请参见:8.2 图的存储与遍历),但这里由于 n 值不大,还可以直接用二进制数表示,这道题用二进制数更简便,原因下面提;
② 状态值:因为 n 值不大,状态使用二进制数表示,比如 n = 5 时,只需要 5 位二进制数表示,例如 00101 表示第 3, 5 盏灯开,第 1, 2, 4 盏灯关。n = 35 时,状态数最大为 2 ^ 35,没有超过 long long 范围。对于 n 盏灯,当且仅当所有灯都打开时,其状态值为 1 << n。为什么要用二进制数?一方面,状态只有 0 和 1 两种,二进制数足够表示所有,同时计算机对二进制的运算有更好的支持,效率会明显高于十进制数,并且使用各类位运算符相当方便,这一点在位运算(请参见:6.1 位运算与进位制)部分有介绍;
③ 状态记录:这里使用 STL 中的 map,映射的是前 n / 2 盏灯的开灯个数和开灯情况二进制数;而对剩余灯枚举时,将 1 << n 减去得到的这部分状态值,并在 map 中查找是否存在,如果存在,即相当于存在前半部分的状态值和后半部分的状态值相加等于灯全部打开的状态值,则将 map 映射的开灯个数和当前后半部分的开灯个数相加,和现有值比较判断是否为更小操作次数,最终得到最小值即为答案。
画图好麻烦,略啦。
代码:
1 #include <bits/stdc++.h> 2 using namespace std; 3 4 #define MAXN 45 5 #define MAXM 1200 6 #define INF 1ll << 30 7 8 typedef long long ll; 9 10 ll n, m, o, u, v, h[MAXN], a, tmp, ans = INF; 11 map <ll, ll> mp; 12 13 class Edge { 14 public: 15 ll v, nxt; 16 } e[MAXM]; 17 18 void add(ll u, ll v) { 19 o++, e[o] = (Edge) {v, h[u]}, h[u] = o; 20 } 21 22 void dfs(ll d, ll l, ll o) { 23 if (!o && d > n / 2) { 24 mp[a] = l; 25 return; 26 } 27 if (o && d > n) { 28 if (mp.count((1ll << n + 1) - a - 2)) 29 ans = min(ans, l + mp[(1ll << n + 1) - a - 2]); 30 return; 31 } 32 ll tmp = a; 33 a ^= 1ll << d; 34 for (ll x = h[d]; x; x = e[x].nxt) { 35 ll v = e[x].v; 36 a ^= 1ll << v; 37 } 38 dfs(d + 1, l + 1, o); 39 a = tmp; 40 dfs(d + 1, l, o); 41 } 42 43 int main() { 44 cin >> n >> m; 45 for (ll i = 1; i <= m; i++) 46 cin >> u >> v, add(u, v), add(v, u); 47 dfs(1, 0, 0); 48 a = 0; 49 dfs(n / 2 + 1, 0, 1); 50 cout << ans; 51 return 0; 52 }
(这份代码与前面描述的略有区别的地方是,状态值二进制数没有使用最低位 2 ^ 0,故运算上有不同)
此题还有另一种解法:DFS + 高斯消元(请参见:<施工中>)。
再来一道。
【例子】小升给同学送礼物,一共准备了 n 个礼物,第 i 个礼物重量为 w[i]。小升从寝室里一次可以拿重量之和不超过 W 的任意多个礼物,他想尽可能拿尽量重的物品,求最大重量。
这种题目类型的正解通常是动态规划(请参见:4.1 动态规划基础 / 记忆化搜索),但这里将数据范围进行修改:n <= 46, W = 2 ^ 31 - 1,和前面那道题一样,n 值很小的同时值域很大,动态规划空间复杂度为 O(W),显然存不下;暴力 DFS 时间复杂度不行;所以这里同样适用折半搜索。
思路:和上题一样,先对前 n / 2 的礼物直接枚举搜索,并记录状态,再搜索后面部分的礼物,即将两部分的状态合并即,具体不过多阐述,并且这道题相比之下更轻松,因为状态值就是该部分礼物的总重量。
代码略。
3、迭代加深搜索
每次限制搜索深度,如果没有解,则累加限制深度,并重新开始搜索。只基于 DFS。
这让人容易联想到 BFS —— 每次优先遍历当前深度的结点,再进入下一层。确实,迭代加深 DFS 就可以看成用 DFS 实现的 BFS,但两者也各有优劣。
BFS 使用队列实现,空间需求是很高的,如果图较为复杂,则可能需要扩展大量的结点;而迭代加深 DFS 相当于用更高的时间复杂度换取更低的空间复杂度,所以做题究竟选择哪一种算法,则需要根据题目的时间空间要求来决定了,但一般情况下 BFS 的空间需求是能满足的。
适用于空间限制较小的情况。
大致流程:
> 设定限制深度为 1,开始搜索
> 搜索函数
① 如果当前深度大于设定深度,返回
② 扩展下一层结点,当前深度 + 1
> 得到答案,程序结束,否则限制深度 + 1,重新搜索
4、启发式搜索
启发式:英文为 heuristics,指依据有限的知识或者不完整的信息在短时间内找到问题解决方案的技术。
这是一个很大的议题,不仅仅局限在某一个领域中。
在计算机科学中一个最基础的目标——发现可证明运行效率良好且可得到最优解的算法。比如解决最短路径问题的 Dijkstra 算法,SPFA 算法,比如解决区间问题的差分/树状数组/线段树,比如上述的各种改进搜索算法,其目的都是在保证得到最优解的前提下降低时间/空间复杂度。
启发式算法,是指基于现有经验来选取当前的较优解,或删去无效解,并且可能会根据趋势随时调整选取方案,不仅让人联想到人工智能、机器学习等概念。
启发式搜索,本身并非一种明确的搜索算法,下面会以比较基础而常见的 A* (A-Star) 算法举例。除了 A*,还有诸如“局部择优搜索法”,“最好优先搜索法”等,均属于启发式搜索。
但是,启发式算法并非都是保证正确性的,由于使用到了贪心的思想,在某些情况下可能得到较差的答案,或者效率低下不亚于普通搜索。迄今,研究启发式算法,乃至对人工智能,机器学习的研究,如何保证正确性的同时尽可能提高效率,是计算机科学领域的一个重要议题。
下面重点介绍启发式搜索中的 A* 算法。
A* 算法是基于 BFS 的改进算法,其核心在于,定义一个评估函数 h(x),将该函数与 g(x),从起点到当前结点路径实际代价,相加得到 f(x),即 f(x) = g(x) + h(x),作为搜索方向的选择标准,它可以引导搜索往理论上更有可能得到解的路径走,即剔除一些偏离的路线。评估函数不是确定的,取决于题目对搜索的需求。
【例子】给出一个 n * m 的 0 - 1 矩阵,如图 a,小明从起点出发,1 能通过 0 不能通过,求问小明走多少步能到达终点。

此图橙色点表示起点,绿色点表示终点。在下面的图示中,为了更好展示,标识的是 f 值而非 0 - 1。
首先是肯定可以用普通 DFS 或 BFS 实现的,现在的任务是,如何提高效率?
前面提了 A* 需要定义一个评估函数,这道题的评估函数定义为:h(x) 表示结点 x 到终点的曼哈顿距离(曼哈顿距离指在标准坐标系上的绝对轴距总和,即两点 x 值差值绝对值和 y 值差值绝对值之和),而代价函数 g(x) 为搜索到结点 x 时的搜索深度,将它们相加得到 f(x),那么如何使用这个函数进行搜索呢?BFS 使用的数据结构是队列,A* 也是一样吗?
将起点加入队列,对于每一个扩展出的新结点记录其 f 值,如图 b,分别为 5, 5, 7, 7,也就是说,在这一轮评估中,上、右方的两个结点更优(从图中也可以看出向右上方走确实是更优的),将这些结点全部加入队列。普通 BFS 中,我们下一层的遍历并不需要考虑孰优孰劣,故使用先进先出的队列即可,而这里加入了 f 值,显然我们需要优先搜索 f 值较小的数,队列的特性并不满足我们的需求,所以 A* 使用的是优先队列 priority_queue(又称为堆,请参见:7.4 堆与优先队列),每次从队列中选出 f 值最小的,目前上、右方两个结点 f 值相等,我们假设选择右边的,如图 c。
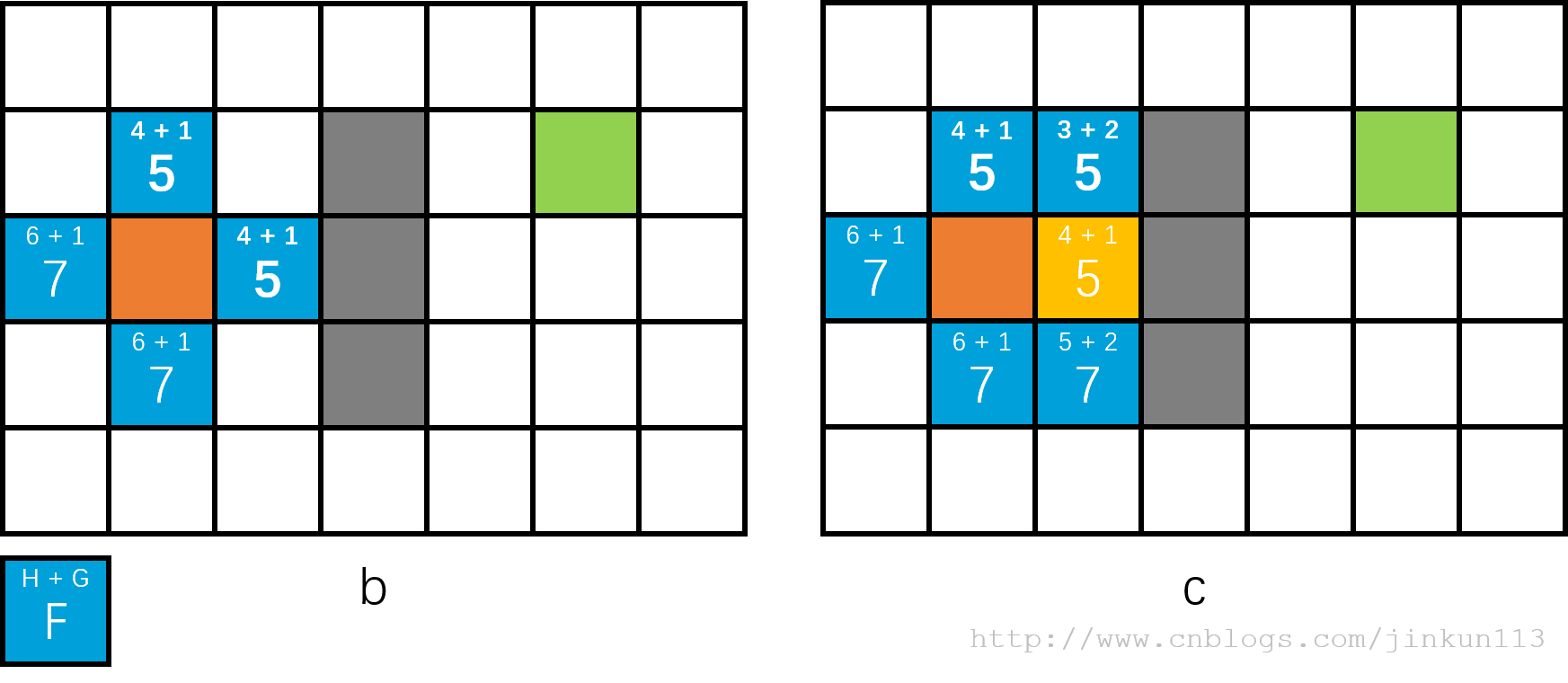
从这一点开始,我们进一步扩展了两个结点,上下方的 f 值分别为 5 和 7,同样我们在这两个 5 中任意选择一个进行下一轮扩展即可,以此类推,如图 d, e,即搜索到终点的整个流程。
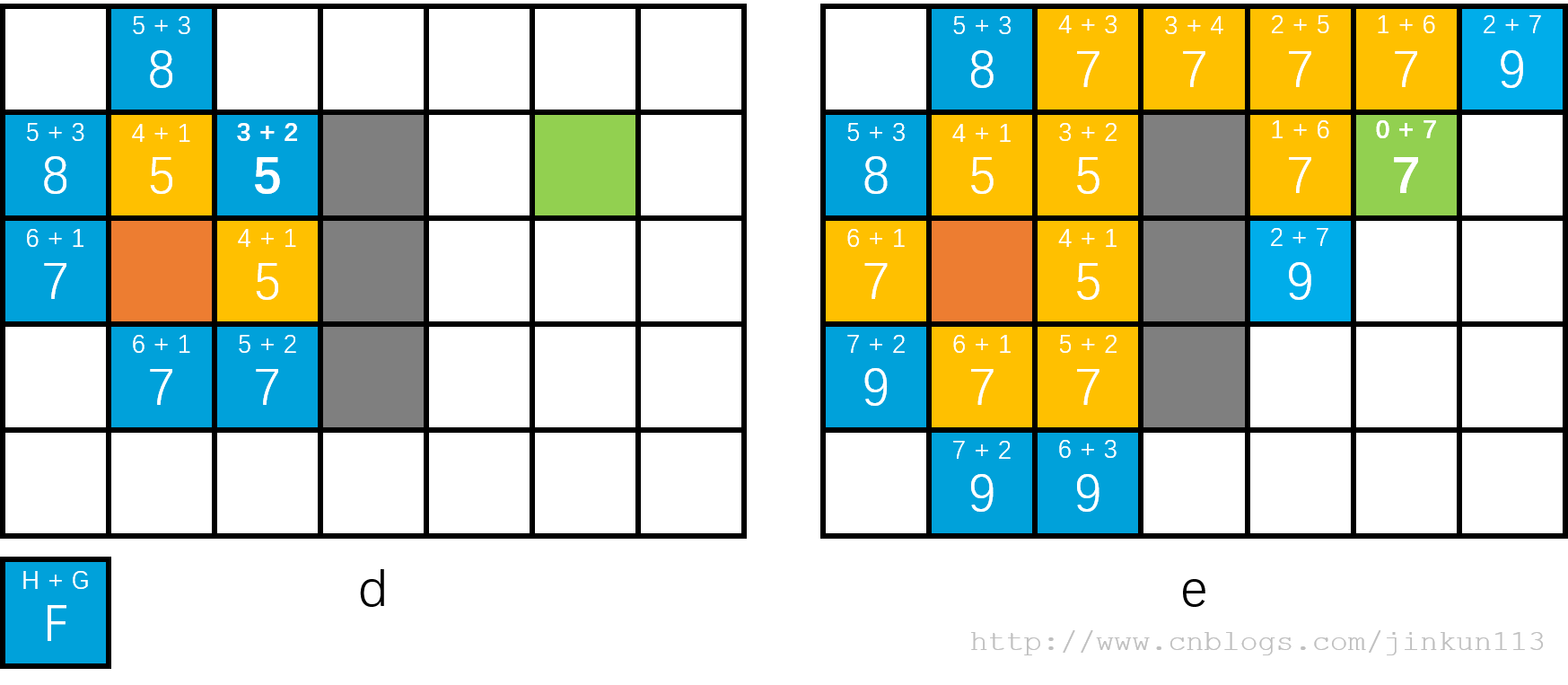
再来看看直接 BFS 的图示,数字为搜索深度,如图 f,总共需要遍历 24 ~ 28 个结点(同层结点可能有先后顺序差异)。
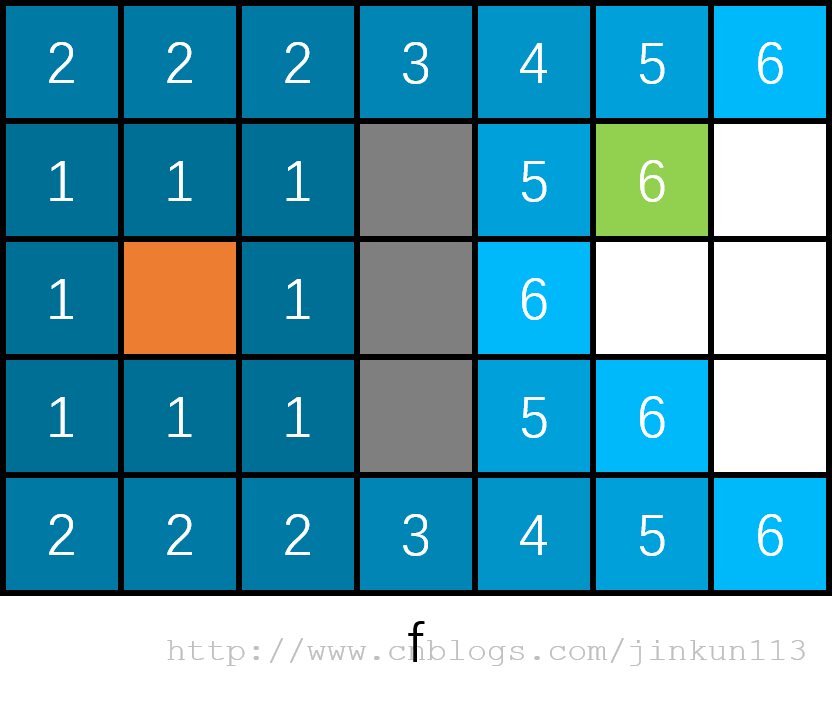
相比之下,A* 只需要遍历 17 ~ 19 个结点就得到了结果,诸如左上角,左下角以及下方的许多结点,都是属于偏离的路线,可以显然而见地看出 A* 算法的优越性。
还有一个小细节,根据三角形不等式,对于任何一个结点,如果再次访问到,不可能更优而被再次加入队列,但并非所有题都是这样。
再来一个更经典的例题。
【Luogu P1379】【八数码难题】在 3 * 3 的棋盘上,摆有八个棋子,每个棋子上标有 1 至 8 的某一数字。棋盘中留有一个空格,空格用 0 来表示。空格周围的棋子可以移到空格中,这样原来的位置就会变成空格。给出一种初始布局和目标布局,找到一种从初始布局到目标布局最少步骤的移动方法。(默认目标布局为下图)
本题正解的 h(x) 函数定义为“当前布局 x 的 8 个数字与目标布局的 8 个数字位置不同的个数”,如下图的例子中,初始布局的 h 值为 5。

更具体的步骤和上个例子其实大同小异,只提几点:
① 状态使用一个 9 位十进制数保存而非二维数组,需要转换,但节省了大量空间;
② 使用 map 来映射状态数和搜索深度,相当于一个访问标记数组,因为对于任一结点并非第一次搜到就是最优的!每次扩展新的结点时,如果是未访问过的结点则直接扩展;如果访问过,则判断当前深度和之前访问该结点并记录下来的深度,如果当前深度较小则再次入队列,而保证下一次该结点作为队首结点时必然是最优的。
代码:
1 #include <bits/stdc++.h> 2 using namespace std; 3 4 #define X i / 3 + 1 5 #define Y i % 3 + 1 6 7 class Node { 8 public: 9 int g, h, v; 10 }; 11 12 struct cmp { 13 bool operator () (Node a, Node b) { 14 return a.g + a.h > b.g + b.h; 15 } 16 }; 17 18 priority_queue <Node, vector<Node>, cmp> Q; 19 map <int, int> mp; 20 21 const int b[4][4] = {{0}, {0, 1, 2, 3}, {0, 8, 0, 4}, {0, 7, 6, 5}}; 22 const int vx[4] = {0, 0, 1, -1}; 23 const int vy[4] = {1, -1, 0, 0}; 24 25 int a[4][4], sv, sh; 26 char ch[10]; 27 28 bool chk(int x, int y) { 29 return x > 0 && y > 0 && x < 4 && y < 4; 30 } 31 32 int astar() { 33 Q.push((Node) {0, sh, sv}); 34 while (!Q.empty()) { 35 int ox, oy; 36 Node o = Q.top(); Q.pop(); 37 if (!o.h) return o.g; 38 for (int i = 8; i >= 0; i--) { 39 a[X][Y] = o.v % 10; 40 if (o.v % 10 == 0) ox = X, oy = Y; 41 o.v /= 10; 42 } 43 for (int i = 0; i < 4; i++) { 44 int tx = ox + vx[i], ty = oy + vy[i]; 45 if (chk(tx, ty)) { 46 int tv = 0, th = 0; 47 swap(a[ox][oy], a[tx][ty]); 48 for (int i = 0; i < 9; i++) { 49 (tv *= 10) += a[X][Y]; 50 th += a[X][Y] != b[X][Y]; 51 } 52 bool hav = mp.count(tv); 53 if (hav && mp[tv] > o.g + 1 || !hav) { 54 mp[tv] = o.g + 1; 55 Q.push((Node) {o.g + 1, th, tv}); 56 } 57 swap(a[ox][oy], a[tx][ty]); 58 } 59 } 60 } 61 } 62 63 int main() { 64 cin >> ch; 65 for (int i = 0; i < 9; i++) { 66 (sv *= 10) += (ch[i] - '0'); 67 sh += (ch[i] - '0') != b[X][Y]; 68 } 69 cout << astar(); 70 return 0; 71 }
综上,写好 A* 算法的关键在于定义一个合适的评估函数,即能保证正确性又尽可能地降低时间复杂度。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号