[知识点] 3.1 DFS/BFS搜索

总目录 > 3 搜索 > 3.1 DFS / BFS 搜索

前言

重中之重的一个知识！也是算法设计中非常非常基础的一部分，OI 这么多年一直陪伴在身边，是大部分不能得到正解只求部分分时的最佳选择，通常我们称之为“暴力搜索”，它写起来不伤脑筋，能够处理数据量小的情况，而且有时灵机一动再优化一下，甚至能得到更可观的分数，所以其实就算对算法、理论或者数据结构不太熟悉，单单把搜索用好了，分数并不会太差。

但也因为学的很早，以至于开这一节时不禁思考一个问题——当年到底是先学的 DFS 和 BFS 还是先学的图论？理论上这两个概念是源自图论的，但是其适用范围又绝不局限于图上。

所以，我们姑且认为，这里讲述的 DFS / BFS 是广义上的搜索。

子目录列表

1、DFS 深度优先搜索

2、BFS 广度优先搜索

 

3.1 DFS / BFS 搜索

1、DFS 深度优先搜索

DFS 英文全称为 Depth First Search，中文名为深度优先搜索，是一种用于遍历图或树的算法。其深度优先，是指在遍历过程中优先往深度更高的结点遍历，其相对概念为 BFS（广度优先搜索），会在下面介绍。

但是，DFS 更多时候并非仅仅局限于图论上的遍历——广义上的 DFS，是指用递归实现元素的遍历搜索，两者本质上是有一定差别的。一般将满足如下两种条件的过程称之为 DFS 搜索：

① 递归调用自身，直到搜索到目的地或没有可以搜索的地方

② 对访问过的元素打上访问标记，确保每个点仅访问一次

下面给出两个例子。

【例子】将 n 分解为 3 个不同的正整数，排在后面的数必须大于等于前面的数，求所有方案。比如 6 = 1 + 2 + 3。

这也太简单了？直接写上：

for (int i = 1; i <= n; i++)
    for (int j = i; j <= n; j++)
        for (int k = j; k <= n; k++)
            if (i + j + k == n)
                cout << n << '=' << i << '+' << j << '+' << k << endl;

那如果是分解为 4 个呢？四重循环？

那如果是分解为 m 个，m <= 10呢？写若干重循环显然是治标不治本的，这个时候，DFS 就有用了。

回顾一下递归（请参见：2.2 递归与分治）的思想，其整个过程是一层层地深入，直到得到最终结果。首先我们明确三大核心：

① 当前状态 dfs(int o, int d)

我们将每一重循环视作一层状态，每一层的状态都记录一些数据：当前的层数 d，当前与 n 的差值 o。

当前的层数 d，用于确定停止递归的状态，假设分解成 m 个数，则当 d = m 时说明不能再分解了，直接判断是否满足条件；

当前与 n 的差值 o，用于判断是否满足条件，如果 d = m 的同时 o = 0，说明这 m 个数之和正好为 n，为一种方案，则 ans++。

② 终止条件 d = m

在 ① 中已经提到了。

③ 下一状态 dfs(o - x, d + 1)

对于第 d 层，如果已经选择了 x 作为本层的值，则 d++, o -= x。

同时，因为题干要求数列单调递增，同时为了最后的输出，需要开一个 a 数组来记录每一层的值。

综上，核心代码为：

void dfs(int o, int d) {
    if (d > m) {
        if (!o) {
            cout << n << '=';
            for (int i = 1; i < m; i++)
                cout << a[i] << '+';
            cout << a[m] << endl;
        }
        return;
    }
    for (int i = a[d - 1] + 1; i <= o; i++)
        a[d] = i, dfs(o - i, d + 1);
}

原网站的代码似乎漏洞百出，先判断 n == 0 再判断 i < m 问题很大，其次也应该写 i <= m。

注意到，前面说 DFS 的条件之一是有访问标记，这道题其实并不需要，因为在每一层枚举数的过程中并不会出现访问到曾经访问过的状态。

看到这里发现，DFS 中的 DF —— 深度优先，似乎没体现出来是什么意思。理论上，广义的 DFS 其实并不存在深度优先这个概念。

再来看一道题目。

【例子】给出一个 n * m 的 0 - 1 矩阵，如图 a，小明以其中一个 1 为起点在矩阵中前进，1 能通过 0 不能通过，求问小明能走到多少个 1。

这种类型的 DFS 已经属于狭义的图论 DFS，但由于只是简单的 0 - 1 矩阵，放在这里讲也没有问题，而且能更好理解什么叫做深度优先。

橙色为小明的起点。从该位置开始为 DFS 的第一层，枚举其四个方向，判断是否能够前进——如图 b，向上向下均为 0，不能通过；向左则越界；向右为唯一路径，则进入下一层。

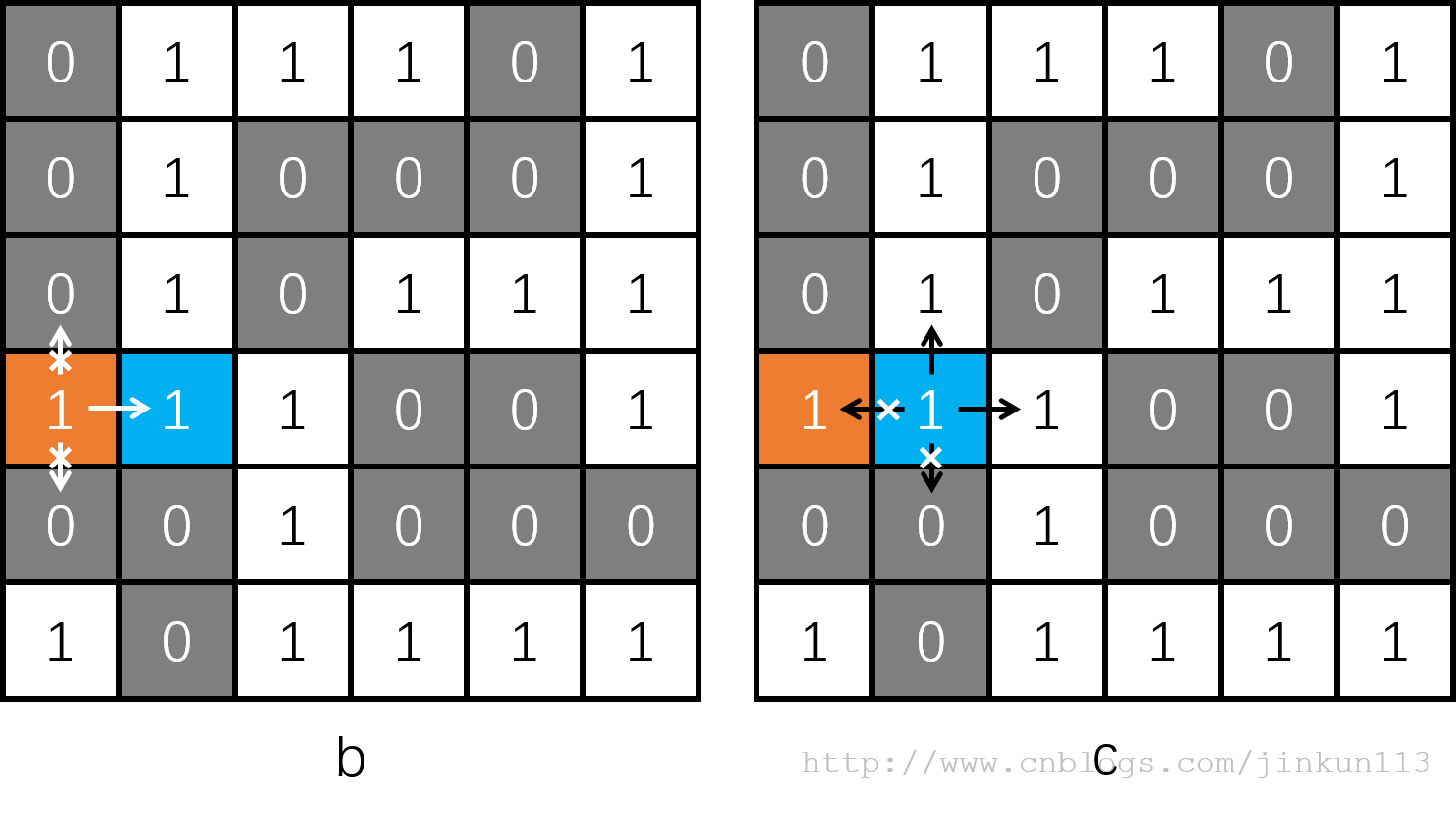
如图 c，当前位置为第二层，向下为 0，不能通过；向左为 1，看起来好像可以走？然后又走到橙色的 1，然后就进入死循环了。

这个时候，访问标记的作用就体现出来了——我们建一个 vis 二维数组，对所有访问过的位置标记为 1，这样在搜索的过程中特判一下，如果该位置的 vis 值为 1，则跳过。如果没有访问标记就会进入死循环，进而栈溢出，这也是写 DFS 最为常见的问题之一。

所以接着就剩下向上和向右两个方向了，它们都可以走，至于先往哪里走，取决于代码的实现。我们假设先往上走，到了第三层，然后以此类推，一直走到了无路可走的地方，如图 d。对于任何一层，如果没有可走的路了，则会返回到上一层，如图 e，我们又回到了之前的位置。

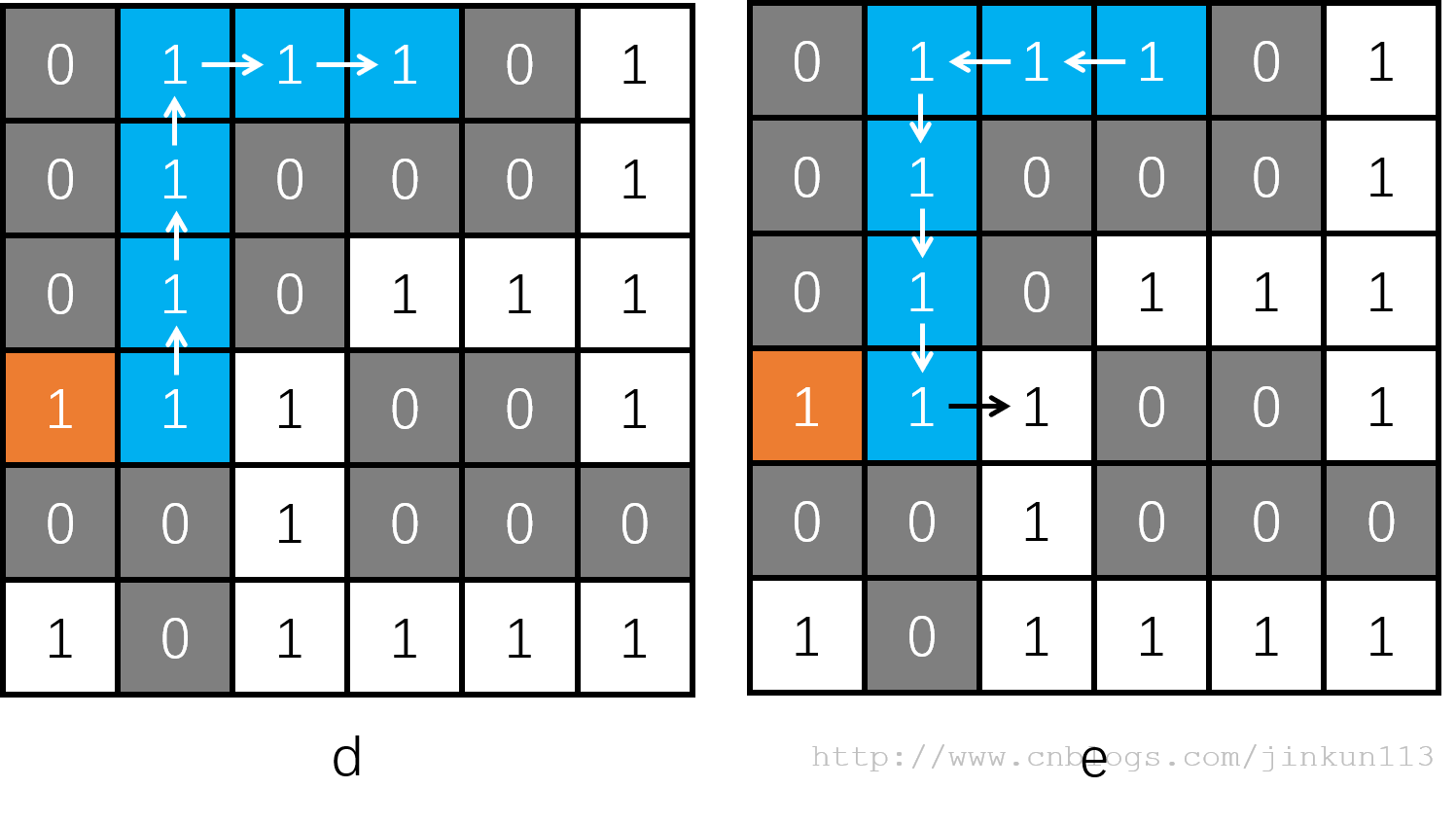
接着只剩向右走的路了，还是一样，最后走到了路的尽头，如图 f。而接下来，我们到过的所有位置都无路可走了，则一路返回到起点，如图 g，最后返回到原函数，DFS 结束。

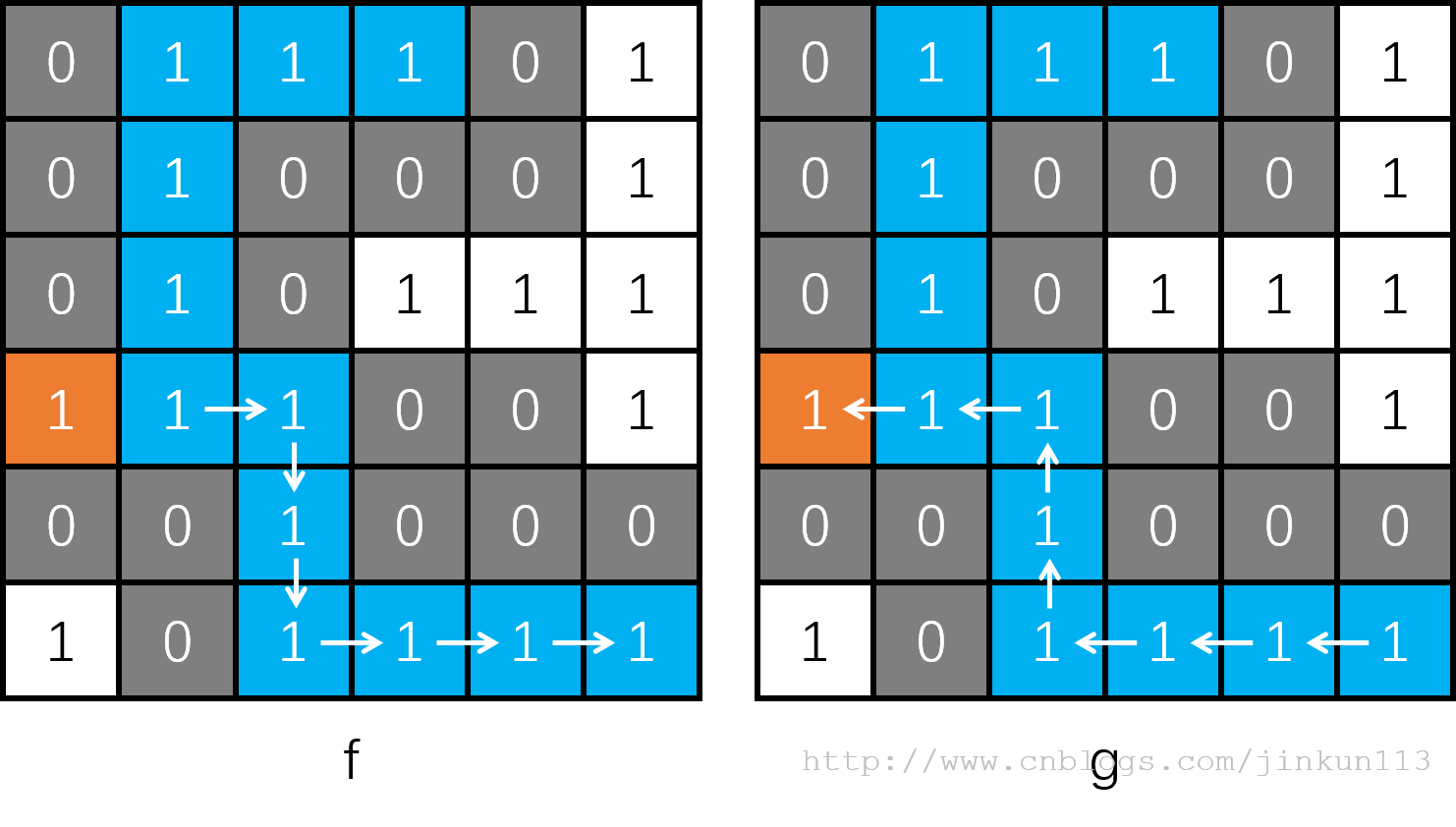
所以深度优先是什么？说白了就是一路走到底，如果发现是死胡同，则原路返回，然后在之前出现过的岔路口选择另一条路，并再次一路走到底，以此往复。

看完大致过程，还是分析下三大核心：

① 当前状态 dfs(int x, int y)

每一层只需要记录当前的位置坐标 x 和 y 即可。

② 终止条件

本题最后只需要累加 1 的个数，不存在终止条件。

③ 下一状态 dfs(x + vx, y + vy)

这也很简单，状态转移只有 4 种可能，即每个坐标的 4 个方向，vx 和 vy 均为 [0, 1]。

核心代码：

const int vx[4] = {0, 0, 1, -1};
const int vy[4] = {1, -1, 0, 0};

bool chk(int x, int y) {
    return x > 0 && y > 0 && x <= n && y <= m && a[x][y] && !vis[x][y];
}

void dfs(int x, int y) {
    vis[x][y] = 1, ans++;
    for (int i = 0; i < 4; i++) {
        int tx = x + vx[i], ty = y + vy[i];
        if (chk(tx, ty)) dfs(tx, ty);
    }
}

代码中的 vx 和 vy 为常量数组，分别表示向四个方向移动。chk 为判断函数，当且仅当下一位置没有越界，没有访问标记且为 1 才会前进。

DFS 本质是用栈实现的，关于栈这个数据结构，请参见：7.1 栈，队列与链表

 

2、BFS 广度优先搜索

BFS 英文全称为 Breadth First Search，中文名为广度优先搜索，和 DFS 一样，是一种用于遍历图或树的算法。BFS 与 DFS 相对，其广度优先是指在遍历过程中优先将当前结点的所有连通结点先访问一遍，再进入这些结点，进行下一轮遍历。

BFS 一般情况下只有狭义部分，即在图/树上进行遍历，这里我们直接拿介绍 DFS 时的第二个例子举例，以便更好认识 BFS 和 DFS 的特点和差别。

还是这个图 a。

橙色为小明的起点。从该位置开始为 BFS 的第一层，枚举其四个方向，如图 b，向右为唯一路径，则进入下一层。

如图 c，当前位置为第二层，向左为 1，同样需要访问标记，该位置 vis 值为 1 了，则跳过，所以接着就剩下向上和向右两个方向了，它们都可以走。

而从下面开始，BFS 就和 DFS 有区别了——接下来，BFS 会同时往上和右走，因为它们同属于第三层，如图 d，图中对结点标识了层数，更好体现遍历关系，而接下来的两条路因为均只有唯一路径，故也没有太多可以广度优先的了，如图 e。

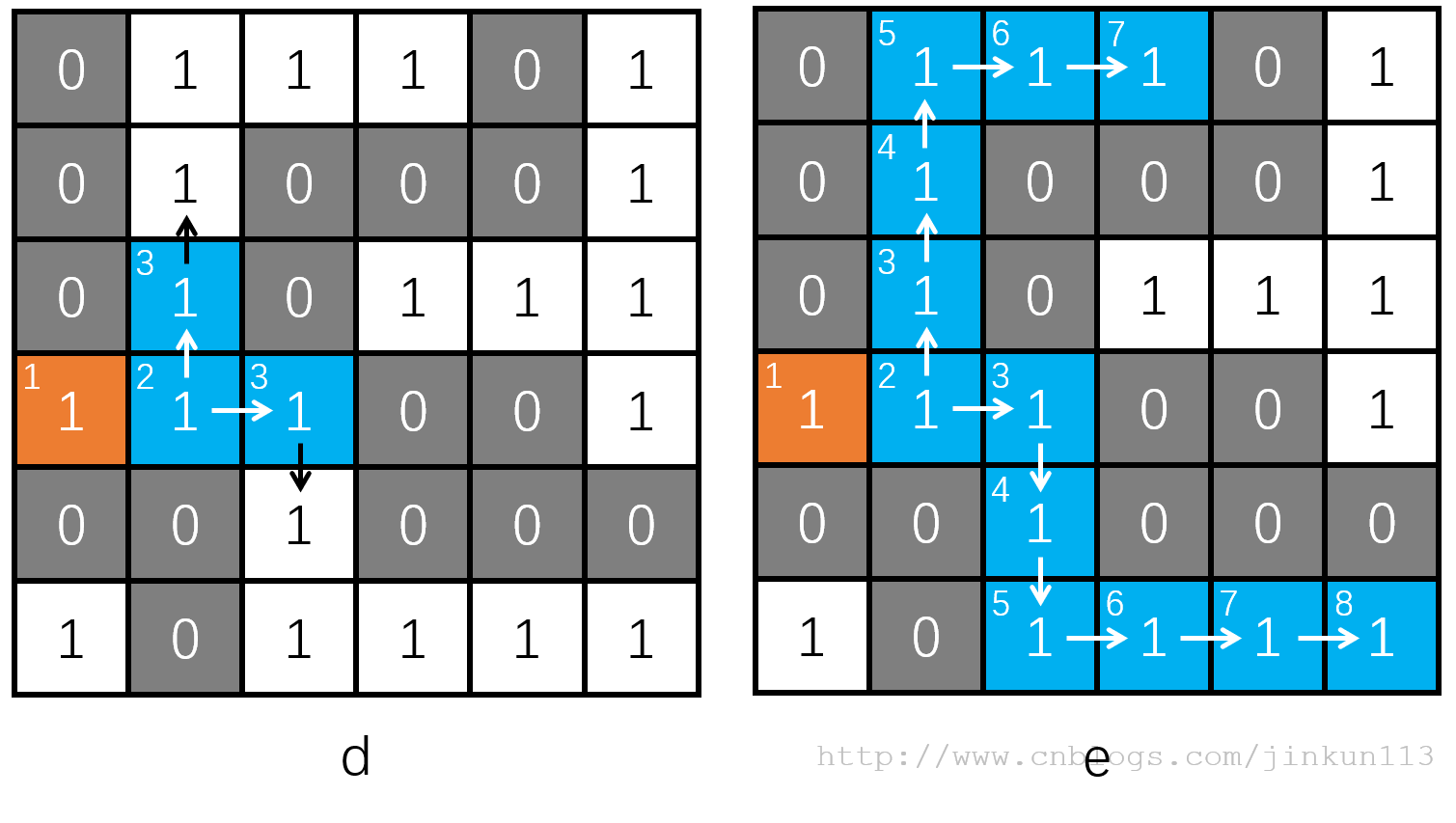
由于这个 0 - 1 矩阵本身是为介绍 DFS 服务的，对于 BFS 而言，根本无法施展拳脚，下面这个地图，DFS 和 BFS 孰优孰劣也便一目了然了。

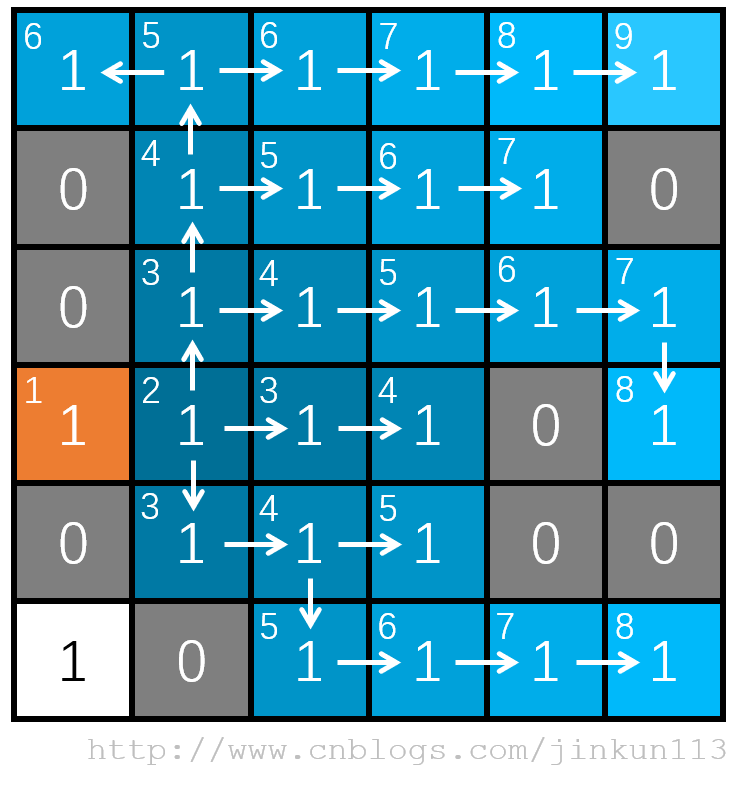
对于较为宽广的地图，BFS 会更为实用。这个例子或许不够明显，我们如果将题目进行改动——小明需要从起点走到终点——在地图的另一个位置，BFS 在这种图中能够较快地在某一层就能遍历到该终点，而 DFS 这种一路走到底的方式很容易在沙漠中迷失自我（当然由于有标记数组的存在，也必然不会迷路）。

而实现方式的话，DFS 使用递归是比较明显的，其对应的数据结构为栈，前面也提了。

而 BFS 本质是用队列实现的，关于队列这个数据结构，请参见：7.1 栈，队列与链表，如果因为不了解队列而看不懂 BFS，看完这篇文章之后一定豁然开朗。

核心代码：

class Node {
public:
    int x, y;
    Node (int _x, int _y) : x(_x), y(_y) {}
    Node () : x(0), y(0) {}
} q[MAXN];

void bfs() {
    int head = 1, tail = 2;
    q[1] = (Node){sx, sy};
    while (head != tail) {
        Node o = q[head];
        for (int i = 0; i < 4; i++) {
            int tx = o.x + vx[i], ty = o.y + vy[i];
            if (chk(tx, ty)) {
                q[tail] = (Node){tx, ty}, tail++;
                vis[tx][ty] = 1, ans++; 
            }
        }
        head++;
    }
}

（chk 函数和 vx, vy 数组见 DFS 核心代码）

关于 0 - 1 BFS 和 优先队列 BFS 暂时不介绍。