[知识点] 2.5 二分思想

总目录 > 2 算法基础 > 2.5 二分思想

前言

一个当时了解得相当晚的思想，乍一看好像和分治差不多味道，其实本质区别还是很大的，当时甚至还有混淆。二分主要是用于二分查找和二分答案，这里还会提一下三分。

子目录列表

1、二分与分治

2、二分查找

3、二分答案

4、三分

 

2.5 二分思想

1、二分与分治

在前面，我们已经提过了分治思想（请参见：2.2 递归与分治），其核心在于对问题进行分解，解决，最后再合并。二分听起来好像是属于分治的一种，但一个最表象的差异在于——分治是递归的，而二分不是；而且，不论是适用情况还是思想核心，两者并无直接关系，下面来看看二分思想是如何体现的。

2、二分查找

二分查找法，又称折半查找法，是在有序数列中查找特定元素的算法。

假设数列为 a[] = {1, 2, 3, 5, 8, 13, 21, 34, 55}，共 9 个数，现在需要查找 55这个数。

如果使用简单的枚举方法来查找，则显然是 O(n) 的，而二分查找能使其降为 O(log n)。

第一轮 a[1..9]：

mid = (1 + 9) / 2 = 5，则第 5 个数为中间值。

a[5] = 8 < 55，则说明 55 必然在中间值的右半部分，因为数列是单调的，则右半部分都是 >= 8 而左半部分都是 <= 8 的。

而对于左右半部分的定义，通常将 [1, mid) 定义为左半部分，即包含中间值，而右半部分定义为 (mid, r]。

第二轮 a[6..9]：

mid = (6 + 9) / 2 = 7（这里采用向下取整），则第 7 个数为中间值。

a[7] = 21 < 55，则说明 55 必然在中间值的右半部分。

第三轮 a[8..9]:

mid = (8 + 9) / 2 = 8，则第 8 个数为中间值。

a[8] = 34 < 55，则说明 55 必然在中间值的右半部分。

第四轮 a[9..9]:

l = r，则可以直接比较，a[9] = 55 = 55，得到答案，返回。

图解：

注意到，二分查找属于整数集上的二分，二分的值是离散的，所以有时其中间值可能是个小数取整，则并非完全均等二分。

代码：

#include <bits/stdc++.h>
using namespace std;

#define MAXN 2005

int n, a[MAXN], o, l, r, mid, ans = -1;

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];
    cin >> o;
    l = 1, r = n;
    while (l <= r) {
        mid = (l + r) >> 1;
        if (o > a[mid]) l = mid + 1;
        else if (o < a[mid]) r = mid - 1;
        else {
            ans = mid;
            break;
        }
    }
    cout << ans;
    return 0;
} 

（代码中的 >> 1 和 / 2 等价，但是速度更快，请参见：6.1位运算与进位制）

然而，这种最基本的二分却只能解决无重复元素的情况，比如在 a[] = {1, 2, 2, 2, 4} 中查找 2 的话，这种二分只能找到第三位的 2，这个问题出在进行二分时的边界设定问题。

将核心代码稍微修改一下：

#include <bits/stdc++.h>
using namespace std;

#define MAXN 2005

int n, a[MAXN], o, l, r, mid;

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];
    cin >> o;
    l = 1, r = n + 1;
    while (l < r) {
        mid = (l + r) >> 1;
        if (o > a[mid]) l = mid + 1;
        else r = mid;
    }
    cout << l;
    return 0;
} 

注意出现了如下几个不同：

① L12: r = n + 1（原为 r = n）

② L13: l < r（原 l <= r）

③ L16: o < a[mid] 时，r = mid（原 r = mid - 1）

④ L16: o = a[mid] 时不返回，而是和 a < a[mid] 时一样 r = mid

下面来解释下原因：

原来的二分算法中，我们对于每一个区间的 l 和 r，其实是表示 [l, r]，即左右均是闭的；而在这里，l 和 r 表示的区间时 [l, r)，是不包括 r 的，这样，对于 ① 和 ③，就不难理解为何要在原基础上 + 1；对于 ②，因为原来的 l <= r 是将 l > r 作为终止条件，而现在是 l == r 时也可以终止了，因为 l == r 时 [l, r) 并无意义。

④ 的区别是关键——在原来的算法中，我们是只要找到相等元素就完工退出，而现在我们即便是找到了，依旧向左半部分的区间继续寻找，目的是找到最左端的相等元素。

下面给出两个图来体现两种二分的查找结果的区别：

如果需要找最右端的呢？把上述所有对右端点的修改改成左端点就行了。

 

3、二分答案

除了查找元素，二分的作用还可以扩展到更广。上述的二分，是在有序离散的数据中查找一个特定值。

先注意到这个“有序”，如果对于一个数列，其一侧均满足某种条件，而另一侧均不满足，其实也可以看作一种有序，而任务就从查找某个特定元素变成找到满足与不满足之间的分界线。

见如下例题：

【POJ2456】【Aggressive cows】一条线段上有 n 个点，选取 m 个点，使得任意相邻点之间距离中的最小值最大（题目大意）。

看起来毫无头绪，起码之前我是不知道这就是二分的模板题：我们先假设这个最小值的最大值为 k，则说明我们选取的这 m 个点任意相邻距离均不会超过 k；同时，也说明如果这个值大于 k，则必然选不到 m 个点；而如果这个值小于 k，则不是最优解。这听起来好像满足上面对于二分算法的使用条件：一侧均满足，一侧均不满足，而这个 k，就是这个分界线。

k 值最小可能为 1，最大可能为这 n 个点的最左端和最右端的距离，将它们设为初始区间的 l 和 r，然后进行二分，直到找到 k 值。

代码：

#include <iostream>
#include <cstdio>
#include <algorithm> 
using namespace std;

#define MAXN 100005

int n, m, a[MAXN], l, r, ans;

bool judge(int k) {
    int o = a[1], tot = 1;
    for (int i = 2; i <= n; i++)
        if (a[i] - o >= k) {
            o = a[i], tot++;
            if (tot >= m) {
                ans = k; 
                return 1;
            }
        }
    return 0;
}

int main() {
    while (~scanf("%d %d", &n, &m)) {
        for (int i = 1; i <= n; i++) cin >> a[i];
        sort(a + 1, a + n + 1);
        l = 1, r = a[n] - a[1];
        while (l <= r) {
            int mid = (l + r) >> 1;
            judge(mid) ? l = mid + 1 : r = mid - 1;
        }
        cout << ans << endl;
    }
    return 0;
} 

这种类型的求解，称作“二分答案”。而这种类型的题目，是二分答案最经典的题型之一——最小值最大（或最大值最小）的求解。

和查找元素的一点区别在于，元素是确定的，找到了可以直接返回；而找分界线不同，二分过程只能得知满足与不满足，所以要尽可能无限逼近答案。

再来说“离散”。上述查找元素和例题，元素本身都是离散的，所以还延伸出了开区间和闭区间的结果差异，但二分同样可以处理连续的数据，即可以出现浮点数。处理浮点数方便在二分时左右端点直接赋值为 mid 即可，但同时要注意由于存在精度问题，所以循环条件写 l <= r 是不合适的，而应根据题目的精度要求写成诸如 abs(l - r) <= 1e-6（l 和 r 的差值小于 10 ^ -6）的形式。这里不单独给出例子，可以大概参考下面的三分的例题便是连续的。

二分思想本身是通俗易懂的，但是细节比较多，对于左右端点的转移方式和终止条件的书写都是因题而异的，在做题时要多加留意，实在不行可以多试几种不同的情况进行调试。

 

4、三分

一种我还从未应用过的玄学操作。二分是用来求单调序列的特定值，而三分是用来求凸函数的最值。直接看一道例题来体会：

【Luogu P3382】【三分法】给出一个 n 次函数，保证在范围 [l, r] 内存在一点 x，使得 [l, x] 上单调递增，[x, r] 上单调递减。试求出 x。

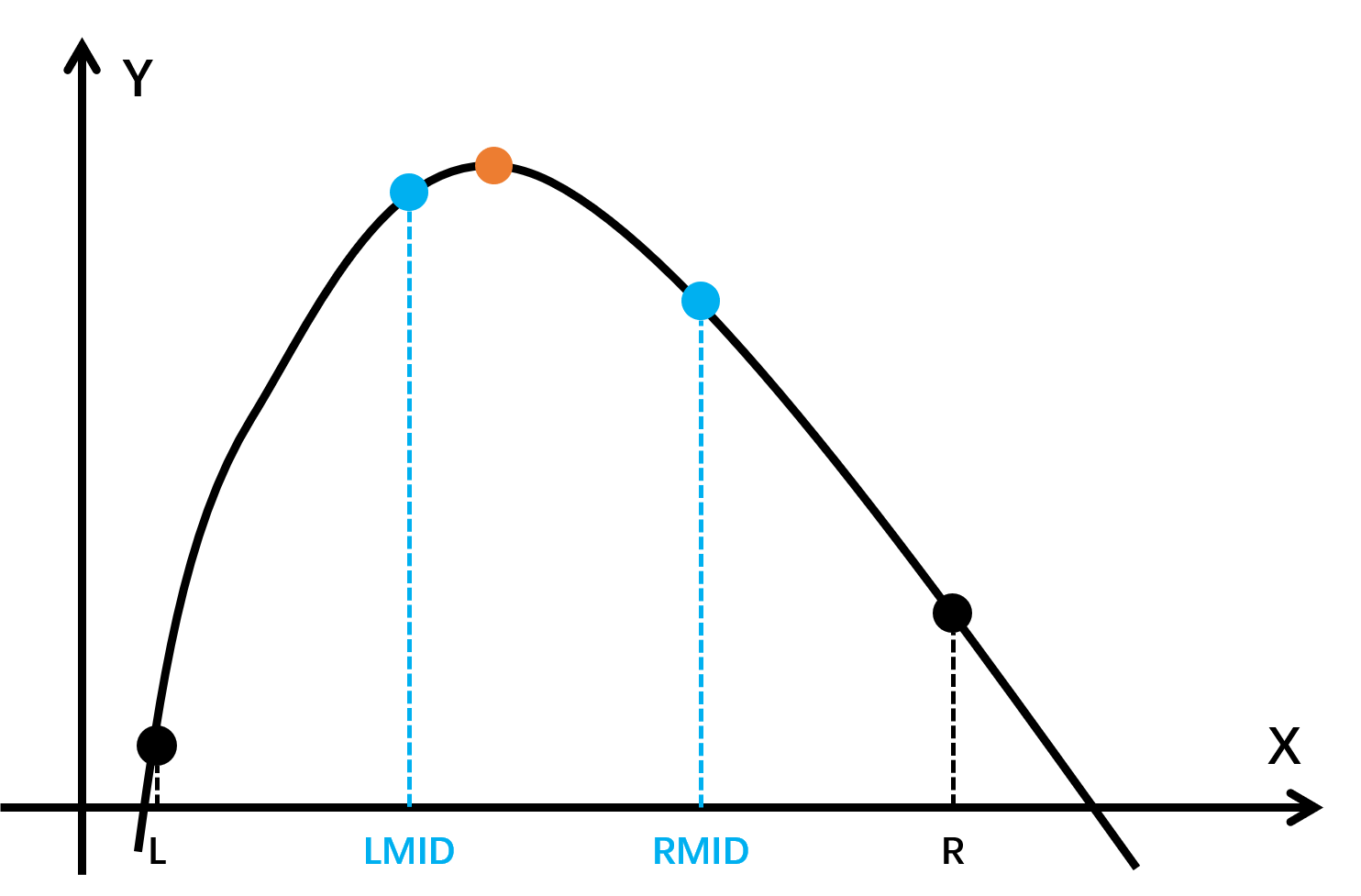
随手搓了个函数，来展现一下三分法的神奇：

首先将给出的 l 和 r 作为左右端点，然后算出区间的两个三等分点 lmid, rmid；

对比 f(lmid) 和 f(rmid) 的值，如果 f(lmid) < f(rmid)，则答案在 [lmid, r] 中，否则在 [l, rmid] 中，再进一步三分。为什么这样判断呢？

如上图所示，如果 lmid 和 rmid 分别在最值的两边，那么答案则必然在 [lmid, rmid] 之中，所以其实不论选那一部分都是一样的；

而如果 lmid 和 rmid 在最值的同一侧，如果满足 f(lmid) < f(rmid)，则必然存在 f(lmid) < f(rmid) < max，那么 max 属于 [lmid, r] 就显而易见了；反之亦然。

代码：

#include <bits/stdc++.h> 
using namespace std;

#define MAXN 15

int n;
double l, r, a[MAXN];

double f(double o) {
    double res = 0, x = 1;
    for (int i = n + 1; i >= 1; i--)
        res += x * a[i], x *= o;
    return res;
}

int main() {
    cin >> n >> l >> r;
    for (int i = 1; i <= n + 1; i++) cin >> a[i];
    while (abs(l - r) > 1e-6) {
        double lmid = l + (r - l) / 3.0;
        double rmid = r - (r - l) / 3.0;
        f(lmid) < f(rmid) ? l = lmid : r = rmid;
    }
    cout << fixed << setprecision(5) << l;
    return 0;
}