[知识点] 4.3 动态规划基础模型——区间DP/LIS/LCS
总目录 > 4 动态规划 > 4.3 区间 DP / LIS / LCS
前言
本文主要介绍动态规划的其他几种基础模型——区间 DP、LIS、LCS。区间 DP,LIS 和背包 DP 一样都是线性动态规划(背包 DP 虽然也可以是二维数组,但其实质依然是线性的),相比之下,它们的状态转移更为复杂,而非简单的单向线性递推;而 LCS 是二维的,但递推方式比较简单。
子目录列表
1、区间 DP
2、LIS
3、LCS
4.3 区间 DP / LIS / LCS
1、区间 DP
[NOI 1995] 在一个环上有 n 个数 a1, a2, ..., an,进行 n - 1 次合并操作,每次操作将相邻的两堆合并成一堆,能获得新的一堆中的石子数量的和的得分。你需要最大化你的得分。
之前在 4.1 动态规划基础 中就有提到做 DP 的最核心步骤,第一步便是划分状态。
我们对这个合并的过程进行倒推:最终状态为进行了 n - 1 次合并,将[1, n] 这 n 堆数合并成了 1 堆。其中最后一次合并为将 [a1, ai] 和 [ai + 1, an] 两堆合并在一起,i 可以为 [1, n - 1] 的任意整数。其中,[a1, ai] 为 [a1, aj] 和 [aj + 1, ai](j 为 [1, i - 1] 的任意整数)合并而成,以此类推,这样我们就将整个问题拆分成若干个子问题了,而每个子问题包含两个变量:左端点 l 和 右端点 r,状态就设计好了,而转移方式也很一目了然。所以,可以得到:
状态数组:f[i][j] 表示 “区间 [i, j] 所有数合并在一起得到的最大的分”;
状态转移:f[i][j] = max(f[i, k] + f[k + 1, j] + sum[j] - sum[i - 1]),k 可以为 [i, j - 1] 的任意整数,sum 表示 a 的前缀和。
之前的推算步骤为倒推,所以在状态转移时应从 i = j 的情况开始处理,即 len = 1,而后从 1 到 n 枚举 len,总时间复杂度为 O(n ^ 3)。
代码:
1 #include <bits/stdc++.h> 2 using namespace std; 3 4 #define MAXN 105 5 6 int n, a[MAXN], sum[MAXN], f[MAXN][MAXN]; 7 8 int main() { 9 cin >> n; 10 for (int i = 1; i <= n; i++) 11 cin >> a[i], sum[i] = sum[i - 1] + a[i]; 12 for (int len = 1; len <= n; len++) 13 for (int i = 1; i <= 2 * n - 1; i++) { 14 int j = i + len - 1; 15 for (int k = i; k < min(j, 2 * n); k++) 16 f[i][j] = max(f[i][j], f[i][k] + f[k + 1][j] + sum[j] - sum[i - 1]); 17 } 18 cout << f[1][n]; 19 return 0; 20 }
2、LIS 最长上升子序列
> 概念和 O(n ^ 2) 算法
最长上升子序列(Longest Increasing Subsequence),指在一个给定的数值序列中,找到一个子序列,使得这个子序列元素的数值依次递增,并且这个子序列的长度尽可能大。最长递增子序列中的元素在原序列中不一定连续。
举个例子,对于数组 a[] = {4, 2, 3, 1, 5},其 LIS 为 {2, 3, 5},长度为 3。
相比之下,LIS 的状态构建和转移比区间 DP 似乎更好理解。由于 LIS 单调递增,所以转移时必然是从较小的数转移而来。比如例子中的 a[3] = 3,可以从 a[2] = 2 转移而来;a[5] = 5,可以从 a[1] = 4, a[2] = 2, a[3] = 3, a[4] = 1 转移而来;那么,直接定义一个一维数组记录当前位置的 LIS 长度即可。
状态数组:f[i] 表示 “序列前 i 个数的 LIS 长度”;
状态转移:f[i] = max(f[j]) + 1,其中 j ∈ [1, i),且 a[j] < a[i]。
时间复杂度为 O(n ^ 2)。
核心代码:
1 for (int i = 1; i <= n; i++) 2 for (int j = 1; j < i; j++) 3 if (a[j] < a[i]) f[i] = max(f[i], f[j] + 1);
最终结果为 f[n] + 1。
不过,这并非最优解。
> 二分优化
由于数列本身没有单调性,不能直接使用二分。令 f[i] 表示 “LIS 长度为 i 时末尾的数”。
还是上方的例子。开始枚举:
① a[1] = 4:i = 1,即 f[1] = 4;
② a[2] = 2:2 < 4,由于对于后面的数而言,2 显然更优(即 > 4 的数是 > 2 的数的子集),所以直接替换,即 f[1] = 2;
③ a[3] = 3:3 > 2,可以构成递增子序列,直接加入,f[2] = 3,说明 LIS 长度为 2 时末尾数为 3;
④ a[4] = 1:1 > 3,不可递增,从头比较:1 > 2,同②,直接替换,f[1] = 1;
⑤ a[5] = 5:5 > 3,同③,直接加入,f[3] = 5.
所以,最终答案为 3。
(越写越觉得这不像 DP。。)
其本质是持续维护一个 LIS,如果当前数比这个 LIS 最末尾数(最大数)更大,直接加入;如果小,则在 LIS 之中找到刚好比它大的一个数替换掉。
感觉其实这不算 DP 了,更像贪心的思路套上 DP 的模板,但还是写在这提供一种思路吧。
暴力做的话同样也是 O(n ^ 2),好就好在 LIS 本身是单调的,所以在 LIS 中查找时可以直接二分,这样就可以做到 O(n log n) 了。
代码:
1 #include <bits/stdc++.h> 2 using namespace std; 3 4 #define MAXN 105 5 6 int n, o, m, f[MAXN], top; 7 8 int main() { 9 cin >> n; 10 for (int i = 1; i <= n; i++) { 11 cin >> o; 12 if (o > f[top]) top++, f[top] = o; 13 else { 14 int l = 1, r = top; 15 while (l <= r) { 16 m = (l + r) >> 1; 17 if (o < f[m]) { 18 if (o < f[m - 1]) r = m; 19 else { 20 f[m] = o; 21 break; 22 } 23 } 24 else l = m + 1; 25 } 26 } 27 } 28 cout << top; 29 return 0; 30 }
3、LCS 最长公共子序列
> 概念
最长公共子序列(Longest Common Subsequence),指在两个给定的数值序列中,找到一个两个序列都包含的公共子序列,使得这个子序列元素的数值依次递增,并且这个子序列的长度尽可能大。最长递增子序列中的元素在原序列中不一定连续。
例如:a[] = {1, 2, 3, 3, 5}, b[] = {1, 4, 3, 5, 2},它们的 LCS 为 {1, 3, 5}。
> 二维动态规划
其实几维并不重要,这里强调是二维的,是为了给后面较为复杂的动态规划进行铺垫——DP 并不都是线性的,它可以在任何结构上进行状态转移。
延续 LIS 的思路,状态数组包含序列位置和 LCS 长度关系。因为存在两个需要比较的序列,则需要两个变量:
状态数组:f[i][j] 表示 “a 的前 i 位和 b 的前 j 位构成的 LCS 长度”;
状态转移:
观察上方例子:{1, 3, 5} 中,5 是由 a[5] = b[4] = 5 提供的,而b[5] = 2,不影响结果,也就是说,a.len = 5, b.len = 4 时和 b.len = 5 时结果一致,可得:
f[i][j] = f[i][j - 1],if a[i] != b[j];
同理,也可能碰到数组 a 多出不相等的一位,即f[i][j] = f[i - 1][j],if a[i] != b[j];
综上,在两者中取较大值为较优解,即:
f[i][j] = max(f[i][j - 1], f[i - 1][j]),if a[i] != b[j];
3 是由 a[3] = b[3] = 3 提供的,也就是说,a.len = 3, b.len = 3 时结果为 2;而 a[4] = 3 时结果同样不变;那么最后的 5 是 a 和 b 同时往后枚举一位递推得到的,可得:
f[i][j] = f[i - 1][j - 1], if a[i] = b[j]。
语言描述可能有点抽象,下面给出三个图。
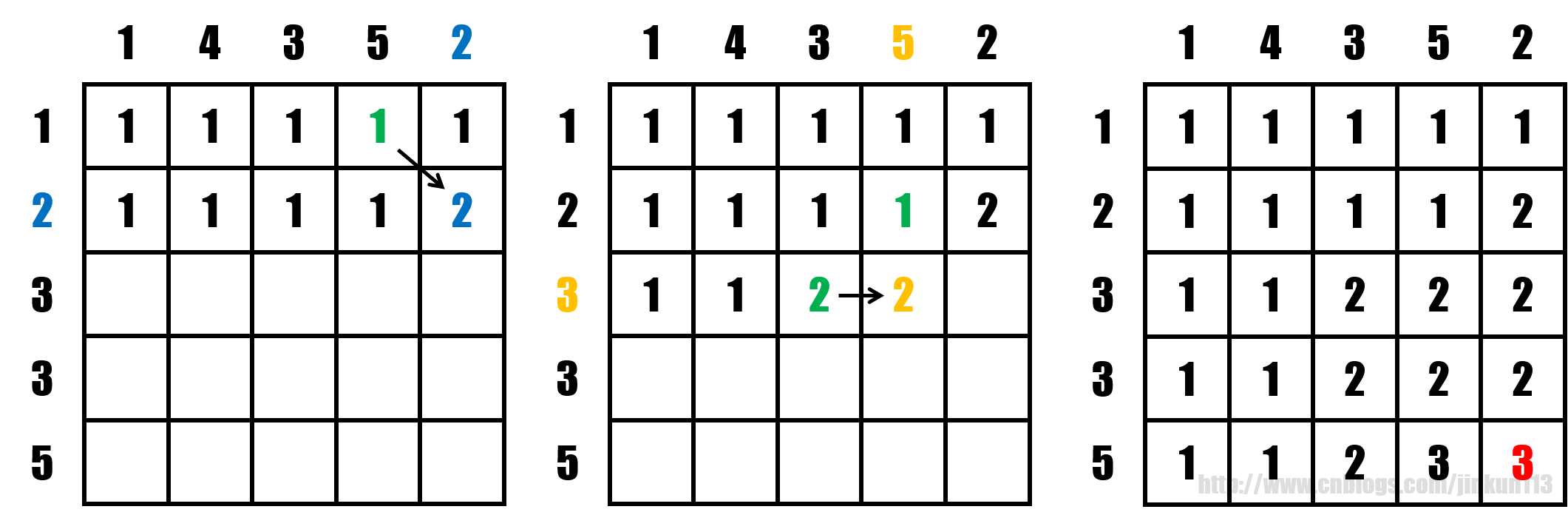
图 1 演示的是第二种情况,即 a 的前 i 位和 b 的前 j 位相等;
图 2 演示的是第一种情况,即 a 的前 i 位和 b 的前 j 位不相等;
图 3 演示的是最终结果,即 ans = f[5][5] = 3;
核心代码:
1 for (int i = 1; i <= n; i++) 2 for (int j = 1; j <= m; j++) 3 f[i][j] = a[i] == b[j] ? f[i - 1][j - 1] + 1 : max(f[i - 1][j], f[i][j - 1]);
最终答案显然为 f[n][m]。时间复杂度为 O(n ^ 2)。



