[知识点] 4.2 动态规划基础模型——背包DP
总目录 > 4 动态规划 > 4.2 背包 DP
前言
本文介绍动态规划集中最基本的模型之一:背包 DP。作为最经典的动规模型,基本所有初学 DP 的最先接触的都是背包问题。
子目录列表
1、什么是背包
2、01背包及滚动数组
3、完全背包
4、多重背包及其优化
5、混合背包
6、二维费用背包
7、分组背包(施工中)
8、有依赖的背包(施工中)
9、其他(施工中)
4.2 背包 DP
1、什么是背包
本类模型的名字出处来源于一道例题:
有 n 个物品和一个容量为 C 的背包,每个物品有重量 c[i] 和价值 v[i] 两种属性,要求选若干物品放入背包使背包中物品的总价值最大且背包中物品的总重量不超过背包的容量。
因为解法经典,故将这类DP称为背包DP。而这道题,只是背包DP其中的一类:因为对于任意物品,只有两种状态——选与不选,即1与0的差别,故称之为0-1背包问题。
2、0-1背包与滚动数组
在 4.1 动态规划基础 中提到的草药例题就是0-1背包问题,只是主体从背包换成了草药,所以这里我们长话短说:
状态数组:f[i][j] 表示“前 i 件物品总重量为 j 时能获得的最大价值”;
状态转移方程:f[i][j] = max(f[i - 1][j], f[i - 1][j - c[i]] + v[i])。
时间复杂度和空间复杂度均为O(n * C)。但有些无良出题方会卡空间限制,这样就促使去想办法压缩下空间了,对于这道题其实也很轻松。
我们注意到在状态转移时,能影响第 i 件物品的状态的,只有第 i - 1 件物品;能影响重量为 j 的状态的,只有小于 j 的重量。f 数组的转移方式如图。
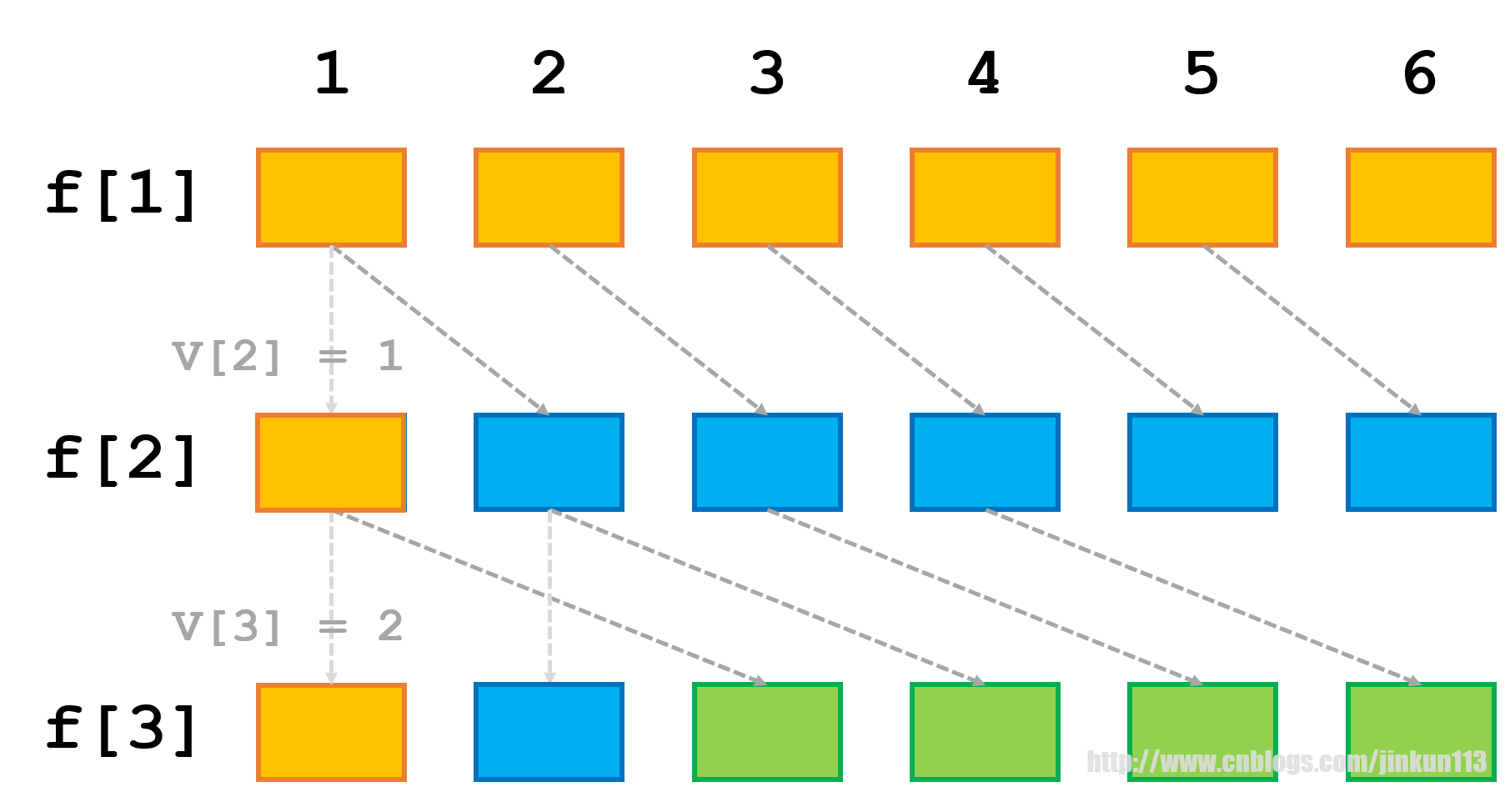
不难发现,数组中的大量数据其实都是一次性的,即转移了一次之后便再也没有被使用过,那我们一直留存在数组中就是对空间的一种浪费了,于是一种奇妙的构造数组的方式就产生了:
滚动数组。
滚动数组 f 只有一维,移除了表示当前物品个数的维度,只保留重量。
相比之下,这个状态更为抽象,需要在原来的二维数组基础上加以理解:
在用二维数组时,在对第 x 个物品状态转移完毕后,f[x][1], f[x][2], ..., f[x][C] 已经填满数据;现在再对第 x + 1个物品进行状态转移,其重量为c[x + 1],从最大重量递减转移,f[x + 1][C] 可从 f[x][C - c[x + 1]](以及f[x][C])转移,f[x + 1][C - 1] 可从 f[x][C - 1 - c[x + 1]](以及f[x][C - 1])转移,以此类推。
据此,我们修改成一维数组:在对第 x 个物品状态转移完毕后,f[1], f[2], ..., f[C] 已经填满数据;现在再对第 x + 1个物品进行状态转移,其重量为c[x + 1],从最大重量递减转移,故f[C] 可从 f[C - c[x + 1]] 转移,由于 f[C - c[x + 1]] 当前仍然存储的是第 x 个物品转移时的数据,直接更新;以此类推,我们发现,和二维数组形式并无差别。
结合图示来理解。

(图本身看起来好像也不是很好理解)
切记,一定是从最大重量开始转移,如果从1开始转移,因为重量是必然往较大值转移,那么新数据就会覆盖掉旧数据,也就是说,就不是从上一层转移下来的了(而是从本层转移过来的,那么这个恰好就是完全背包的情况了,具体见下方介绍)
故,滚动数组的形式和转移方式:
状态数组:f[i] 表示“总重量为 i 时能获得的最大价值”;
状态转移:f[i] = max(f[i], f[i - c[j]] + v[j]), j 表示当前为第 j 个物品。
时间复杂度为O(n * C),空间复杂度为O(C)。
1 #include <bits/stdc++.h> 2 using namespace std; 3 4 #define MAXN 2005 5 6 int n, C, c[MAXN], v[MAXN], f[MAXN]; 7 8 int main() { 9 cin >> n >> C; 10 for (int i = 1; i <= n; i++) 11 cin >> c[i] >> v[i]; 12 for (int j = 1; j <= n; j++) 13 for (int i = C; i >= c[i]; i--) 14 f[i] = max(f[i], f[i - c[j]] + v[j]); 15 return 0; 16 }
3、完全背包
有 n 种物品和一个容量为 C 的背包,每种物品有重量 c[i] 和价值 v[i] 两种属性,要求选若干物品放入背包使背包中物品的总价值最大且背包中物品的总重量不超过背包的容量。每种物品可以选取多次。
和上面的问题差别在于,每种物品可以选多次。最直接的想法是,再增加一个变量 k 表示物品选择个数,依次枚举 k 来转移状态,时间复杂度为 O(n ^ 2 * C),当然这是个很憨批的算法。其实大可不必考虑这个!01 背包中我们状态转移都是当前物品从上一个物品转移过来的,同时记录了不同重量的最大价值,那么可以放入多个相同物品,则可以改成从当前物品自身来转移,比如 f[i][j] 就可以从 f[i][j - c[i]] 转移过来,也可以从f[i][j - 2 * c[i]] 转移,表示取了两个物品 i。那么状态转移时直接在 01 背包的基础上改成:
状态转移方程:f[i][j] = max(f[i - 1][j], f[i][j - c[i]] + v[i])
同样地,也可以使用滚动数组,而更巧妙的是,完全背包和 01 背包的状态转移方程是一模一样的,唯一的区别在于转移方式是重量从小到大。为什么?01 背包的第二层 for 循环是相反的,则不会出现同一个物品多次选择的情况,而完全背包正可以多次选择,循环调为正向,即满足了条件。
代码略。
4、多重背包及其优化
现在在前面背包的基础上再增加一个限定条件——对于第 i 种物品,有且仅有 k[i] 个。
最简单的想法是,把这 k[i] 个物品等价成 k[i] 种相同的物品,之间转换成 01 背包,时间复杂度为 O(n * C * ∑ki)。
二进制分组优化
个人觉得有点倍增的思想。考虑到原做法有个弊端就是,对于这 k[i] 个物品,取其中的第一个加第二个,还是取第二个加第三个,还是。。本质都是等价的,但我们要做很多次这样的重复劳动。现在我们将这些相同的物品进行打包,分别打包成 1 个,2 个,4 个,...,2 ^ n 个,再补上一个多余的包,比如:
k[i] = 7 时,打包成 1 + 2 + 4 个(不用补齐);
k[i] = 10 时,打包成 1 + 2 + 4 + 3 个;
k[i] = 29 时,打包成 1 + 2 + 4 + 8 + 14 个。
然后进行 DP 的时候,就不再是一个个物品进行选择,而是直接选择这些捆绑包,显然 [1, k[i]] 的任何数都能被这些捆绑包的某种组合方式等价,与此同时大幅降低了复杂度。
核心代码:
for (int i = 1; i <= n; i++) { cin >> tc >> tv >> k; o = 1; while (k - o > 0) { tot++, c[tot] = o * tc, v[tot] = o * tv; k -= o, o <<= 1; } tot++, c[tot] = k * tc, v[tot] = k * tv; }
5、混合背包
将上述背包混合在一起,部分物品只有 1 个,部分物品有无限个,部分物品有个数限制。
其实也不难解。多重背包我们已经转换成 01 背包了,那剩下的就是 01 背包和完全背包的区别了,直接在循环物品时判断当前是 01 还是完全,然后分别按照各自的转移方式转移即可,因为物品之间本身就是独立而互不影响的。代码略。
6、二维费用背包
现在将物品放入背包时还增加了一个限制条件——时间。假设装入每一个物品需要花费时间 t[i],要求总装入时间不超过 T。这样时间和重量组成了二维费用,称之为二维费用背包。
直接在原来的转移方程基础上增加一维,即:
状态数组:f[i][j] 表示“总重量为 i,总时间为 j 时能获得的最大价值”;
状态转移:f[i][j] = max(f[i][j], f[i - c[k]][j - t[k]] + v[j]), k 表示当前为第 k 个物品。
7、分组背包
8、有依赖的背包
9、其他



