[知识点] 6.4.2 欧几里得算法与扩欧算法
总目录 > 6 数学 > 6.4 数论 > 6.4.2 欧几里得算法与扩欧算法
前言
没什么好说的啦。
更新日志
Update - 20200728
重整了一下章节之间的逻辑,以及标题进行了替换。
子目录列表
1、欧几里得算法
2、扩欧算法
3、求解
4、应用
6.4.2 欧几里得算法与扩欧算法
1、欧几里得算法
欧几里得算法(Euclidean Algorithm),又称为辗转相除法,用于计算两个正整数 x, y 的最大公约数,公式为:
gcd(x, y) = gcd(y, x mod y)
代码:
1 int gcd(int x, int y) { 2 return y ? gcd(y, x % y) : x; 3 }
同时,你也可以选择使用 algorithm 库中的 __gcd(x, y) 函数。
2、扩欧算法
扩展欧几里得算法(Extended Euclidean algorithm)是欧几里得算法的扩展版本,简称扩欧算法。已知正整数 a, b,求得最大公约数的同时可以求得 x, y(其中一个很可能为负数),使它们满足裴蜀定理:
ax + by = gcd(a, b)
3、扩欧求解
求解方法和欧几里得算法类似,在辗转相除的基础上增加两个数组,具体步骤见下:
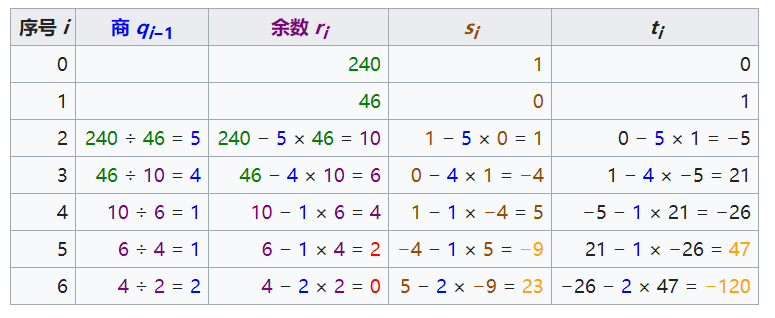
i = 5时,s[i] = -9, t[i] = 47,分别为裴蜀定理中的 x 和 y;余数r[i]为最大公约数。
i = 6时,s[i] = 23, t[i] = -120,用于验证正确性,验证方法:t[i] * (-2) = 240, s[i] * 2 = 46,分别为 a 和 b。
代码 1:
1 int exgcd(int a, int b) { 2 if (!b) return ob; 3 x = oox - a / b * ox, oox = ox, ox = x; 4 y = ooy - a / b * oy, ooy = oy, oy = y; 5 return exgcd(ob = b, a % b); 6 }
(最终的 x 存放在 oox 中,y 同理)
这是根据算法的描述自己写的代码,在参考了更多 wiki 和博客的介绍后,发现 x 和 y 并不需要弄这么多变量来存,而可以先求得最大公约数后反推 x 和 y。
代码 2:
1 int exgcd(int a, int b, int &x, int &y) { 2 if (!b) { 3 x = 1, y = 0; 4 return a; 5 } 6 int res = exgcd(b, a % b, x, y); 7 ox = x, x = y, y = ox - a / b * y; 8 return res; 9 }
4、扩欧应用
① 求线性同余方程
线性同余方程:形如 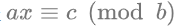 的方程。
的方程。
由于方程和 ax + by = c 是等价的,根据扩展欧几里得定理,存在整数解等价于 gcd(a, b) 整除 c(gcd(a, b) | c)。
所以,根据上述求解方法求得 x 和 y 后,方程两边同时除以 gcd(a, b) 且乘 c,即 cx / gcd(a, b)和cy / gcd(a, b) 为方程的一组解。
(gcd(a, b) = 1,且 x0, y0 为其中一组解时,所有解可以表示为 x = x0 + bt, y = y0 - at,t 为任意整数)
代码略。
② 求乘法逆元
乘法逆元:全称为模意义下的乘法运算的逆元(Modular Multiplicative Inverse),如果一个线性同余方程满足:

则 x 称为 a mod b 的逆元,记作a ^ -1。
作为线性同余方程的一种特殊情况,思路是类似的:方程和 ax + by = 1 是等价的,存在整数解等价于 gcd(a, b) 整除 1,即 gcd(a, b) = 1,即 a 和 b 互素。
代码略。
乘法逆元同样可以用费马小定理来求,请参见:6.4.3 费马小定理



