[知识点] 6.4.3 费马小定理
总目录 > 6 数学 > 6.4 数论 > 6.4.3 费马小定理
前言
没什么好说的啦。
更新日志
Update - 20200728
重整了一下章节之间的逻辑,以及标题进行了替换。
子目录列表
1、定义
2、应用
3、延伸
6.4.3 费马小定理
1、定义
费马小定理是数论中的一个定理:假如a是一个整数,p是一个质数,那么:a ^ p - a是p的倍数,即:
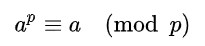
如果a不是p的倍数,还可以表示为:
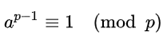
2、应用
① 计算余数
例子:计算 2 ^ 100 / 13 的余数

即余数为3。
② 乘法逆元
关于乘法逆元的概念和扩欧定理求法,请参见:6.4.2 欧几里得算法与扩欧算法
根据费马小定理,可得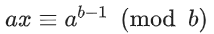 ,进而
,进而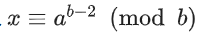 ,直接快速幂求出a ^ (b - 2)的余数即可。
,直接快速幂求出a ^ (b - 2)的余数即可。
3、延伸
费马小定理本质上是欧拉定理的一种特例。
欧拉定理:假如n和a为正整数,且互素,则:
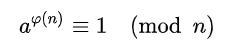
其中,ψ(n)为欧拉函数(欧拉函数:ψ(n)表示小于等于n的正整数中与n互质的数的个数)
在费马小定理的基础上,欧拉定理可以处理模数非质数的情况,比如:
计算7 ^ 222 / 10的余数。
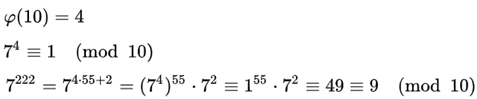



 浙公网安备 33010602011771号
浙公网安备 33010602011771号