[Nowcoder]2020牛客寒假算法基础集训营5
20200213 第五场
进度(7 / 10) 未完成:C / F / G
A、模板
1、链接
https://ac.nowcoder.com/acm/contest/3006/A
2、题面
牛牛,牛可乐和牛能组成了一只队伍参加ACM系列赛事,他们起了一个优雅的队名叫~“牛牛战队”
牛可乐将试图通过以下操作用尽可能少的步骤把一个密钥转换为另一个:
- 将其中任意一个字母替换为另一个
- 把最后一个字母删除
- 在尾部添加一个字母
得到的转化步数就是最后的密码。
一天,你和他们队员一起聚餐,你用可乐把他们灌倒了,从牛牛和牛能口中套出了两个密钥。你要趁他们醒之前拿到模板并复印一份再放回去。你能尽快的算出密码吗?
3、思路
签到题。思路略。
4、代码
1 #include <bits/stdc++.h> 2 using namespace std; 3 4 #define MAXN 100005 5 6 int n, m, ans; 7 char s1[MAXN], s2[MAXN]; 8 9 int main() { 10 cin >> n >> m >> s1 >> s2; 11 for (int i = 0; i < min(n, m); i++) 12 ans += s1[i] != s2[i]; 13 cout << ans + abs(n - m); 14 return 0; 15 }
B、牛牛战队的比赛地
1、链接
https://ac.nowcoder.com/acm/contest/3006/B
2、题面
由于牛牛战队经常要外出比赛,因此在全国各地建立了很多训练基地,每一个基地都有一个坐标(x, y)。
这周末,牛牛队又要出去比赛了,各个比赛的赛点都在x轴上。牛牛战队为了方便比赛,想找一个到达训练基地最大距离最小的地方作为比赛地。
这个问题对于牛牛战队太简单了,它就交给了你,你来帮他算一下~
3、思路
我们设当前的最大距离为r,以每一个训练基地为圆心作半径为r的圆,圆与x轴的交点之间的弦中的所有点到该训练基地距离<=r。将所有的弦求出来,则所有的弦都重合的部分的所有点到所有训练基地距离都<=r。使所有弦恰好有重合部分(即两个或以上的弦正好交于某一点),此时r为最小值。
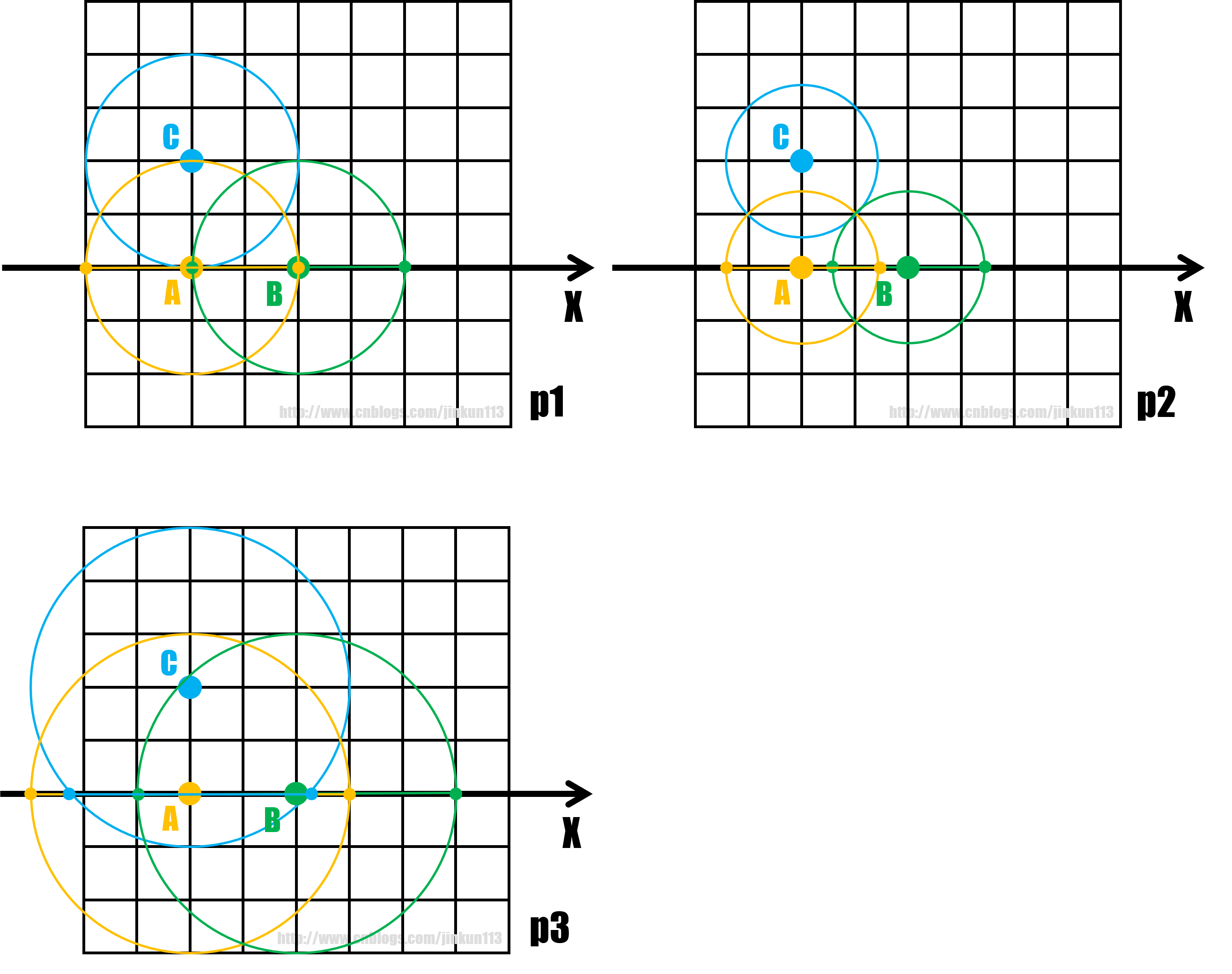
如图所示,p1为三段弦(其中C点与x轴相切)正好重合于A点,此时r = 2,即答案。p2中C点与x轴没有交点,显然这个距离根本到达不了C点,答案会更大;p3并非恰好重合,答案会更小。
根据这个思路,二分答案可以解决。
题解是三分法,不过我不太记得了。
4、代码
1 #include <bits/stdc++.h> 2 using namespace std; 3 4 #define MAXN 100005 5 #define INF 0x3f3f3f3f 6 7 int n; 8 double x[MAXN], y[MAXN]; 9 10 int main() { 11 cin >> n; 12 for (int i = 1; i <= n; i++) 13 cin >> x[i] >> y[i], y[i] = abs(y[i]); 14 double l = 0, r = 100000000; 15 while (r - l > 1e-5) { 16 double m = (l + r) / 2, mi = INF, mx = -INF, f = 0; 17 for (int i = 1; i <= n; i++) { 18 if (y[i] > m) { 19 f = 1; 20 break; 21 } 22 double o = sqrt(m * m - y[i] * y[i]); 23 mi = min(mi, x[i] + o), mx = max(mx, x[i] - o); 24 } 25 if (mi >= mx && !f) r = m; 26 else l = m; 27 } 28 cout << l; 29 return 0; 30 }
D、牛牛与牛妹的约会
1、链接
https://ac.nowcoder.com/acm/contest/3006/D
2、题面
牛牛在辛苦的一天的比赛之后,要去找牛妹玩,其实牛妹那天也在比赛。他为了找到牛妹,要尽快的从自己的比赛地到她的比赛地。
还记得吗,比赛地都是只在x轴上的,所以两个人的坐标都满足y = 0。牛牛除了可以以1单位距离/单位时间的速度移动任意时间以外,还可以花费1单位时间进行闪现。每次闪现时,如果当前他的坐标是x = k,他将闪现到k ^ (1/3)的位置。
请帮他算算,最短需要多少时间,他可以找到牛妹~
3、思路
两种移动的方式:一种直接走过去,耗时等同于距离;一种用跳刀跳过去,耗时为1,我们要考虑的就是什么情况下跳刀会比走过去更划得来,即走过去耗时大于1。
根据题意,跳刀只能变成自身的立方根,即如果是正数只能变小;如果是负数只能变大。我们将a和b所在的位置根据正负和大小关系分成6种情况讨论:
① a < b; a > 0, b > 0.
② a > b; a < 0, b < 0.
这两种情况最简单,因为跳刀被禁用了,所以 ans = abs(a - b)。
③ a < b; a < 0, b > 0.
④ a > b; a > 0, b < 0.
这两种情况可以将路程分成两部分处理,第一部分接近原点,正数变小负数变大,则需要考虑用跳刀;第二部分远离原点,直接走过去。
⑤ a < b; a < 0, b < 0.
⑥ a > b; a > 0, b > 0.
这两种情况,由于在同一侧,用跳刀不能过于贪心,因为你可能跳过身,这个时候要抉择是跳到她面前再走过去,还是跳到她身后再过去。就类似于坐公交车/地铁,如果你要去的地方在车站之间,你就需要考虑下是坐到前一站还是后一站了。
分析完6种情况,判定是用跳刀还是走过去其实就不难了,不做过多分析。
这题坑了我一次,现在才知道pow(a, b)中a不能为负数,因为编译器不会事先判定b的值,直接一刀切的不准a < 0了。那么对于本题就可以用-pow(-a, b)来解决这个问题。
然后fwl提供了个cbrt函数,太冷门了,真的没听过,查都查不到 Orz...
4、代码
1 #include <bits/stdc++.h> 2 using namespace std; 3 4 int t; 5 6 int main() { 7 cin >> t; 8 for (int i = 1; i <= t; i++) { 9 double ans = 0, a, b; 10 cin >> a >> b; 11 if (a < b) { 12 if (a <= 0 && b >= 0) { 13 while (a + pow(-a, 1 / 3.0) < -1.0) a = -pow(-a, 1 / 3.0), ans += 1; 14 ans += b - a; 15 } 16 else if (a >= 0 && b >= 0) ans = b - a; 17 else if (a < 0 && b < 0) { 18 while (abs(-pow(-a, 1 / 3.0) - b) + 1 < abs(a - b)) a = -pow(-a, 1 / 3.0), ans += 1; 19 ans += abs(a - b); 20 } 21 } 22 else if (a > b) { 23 if (a >= 0 && b <= 0) { 24 while (a - pow(a, 1 / 3.0) > 1.0) a = pow(a, 1 / 3.0), ans += 1; 25 ans += a - b; 26 } 27 else if (a <= 0 && b <= 0) ans = a - b; 28 else if (a > 0 && b > 0) { 29 while (abs(pow(a, 1 / 3.0) - b) + 1 < abs(a - b)) a = pow(a, 1 / 3.0), ans += 1; 30 ans += abs(a - b); 31 } 32 } 33 else ans = 0; 34 printf("%.9lf\n", ans); 35 } 36 return 0; 37 }
E、Enjoy the game
1、链接
https://ac.nowcoder.com/acm/contest/3006/E
2、题面
牛牛战队的三个队员在训练之余会自己口胡了一些题当做平时的益智游戏。有一天牛可乐想出了一个小游戏给另外两名队员玩,游戏规则如下:
初始一共有n张卡牌
先手第一步最少要拿1张牌,最多要拿n - 1张牌。
接下来每一步,双方最少要拿1张牌,最多拿等同于上一步对方拿的牌数的牌。
拿走最后一张牌的人将取得游戏的胜利。
你作为旁观者,看着他们玩的很开心,想参与到这场游戏中来,赌一赌谁会能赢。
3、思路
博弈论?打表或者自己模拟找规律。
根据题意,我们来枚举下列情况:
① n = 2;先手拿1张,后手拿1张,先手输;故先手必输;
② n = 3;先手拿1张,后手拿1张,先手拿1张,先手胜;故先手必胜;
③ n = 4;先手拿1张,后手拿1张,情况转化为②,先手输;先手拿2张,后手拿2张,先手输;先手拿3张,后手拿1张,先手输;先手必输。
现在我们可以发现,如果先手拿的牌 >= n / 2,则必输,因为后手可以拿剩下的所有牌,故不用考虑了,而如果 < n / 2,则均可转化为现有情况;
④ n = 5;先手拿1张,情况转化为③,先手胜;故先手必胜;
⑤ n = 6, 7, 8... 以此类推,可得如果 n = 2 ^ k,即先手必输;其他情况先手必胜。
4、代码
1 #include <bits/stdc++.h> 2 using namespace std; 3 4 long long n; 5 6 int main() { 7 cin >> n; 8 while (n % 2 == 0) n >>= 1; 9 cout << (n == 1 ? "Alice" : "Bob"); 10 return 0; 11 }
H、Hash
1、链接
https://ac.nowcoder.com/acm/contest/3006/H
2、题面
这里有一个hash函数
const int LEN = 6;
int mod;
int Hash(char str[])
{
int res = 0;
for (int i = 0; i < LEN; i++)
{
res = (res * 26 + str[i] - 'a') % mod;
}
return res;
}
现给定一个长度为6的仅由小写字母构成的字符串s和模数mod,请找到字典序最小且大于s的一个长度为6的仅由小写字母构成的字符串s',使得其hash值和s的hash相等。
3、思路
根据给出的hash函数,可以理解为将26进制的字符串转换成一个十进制数,再取模。那么当且仅当两个字符串模该模数同余,会有相同的hash值。从右往左的第k位,每增大一个字母(指诸如从'a'到'b'),十进制数就增加26 ^ k,根据这一点从左往右将这个模数加在现有字符串上,模数清零后即下一个hash值相同的字符串。
交了7发才过,被自己蠢到了。结果先是没考虑不存在的情况,接着又是没考虑进位情况,考虑了进位又忘了要从右往左进位,考虑了顺序后又忘了进位可能不止进一次,,等所有东西都考虑到了,再去交发现还是不对,试了各种数据没有任何错误,这我就不懂了,任何转到别的题去了。结果在切题时偶然瞟到一句话——“多组用例,请处理到文件结束。(用例组数大约为1000组左右)”。我的天。
4、代码
1 #include <bits/stdc++.h> 2 using namespace std; 3 4 char ch[8]; 5 int m, a[8], ans[8]; 6 7 int main() { 8 while (cin >> ch + 1 >> m) { 9 memset(ans, 0, sizeof(ans)); 10 for (int o = 11881376, i = 1; o >= 1; o /= 26, i++) 11 a[i] = m / o, m %= o; 12 for (int i = 6; i >= 1; i--) { 13 ans[i] += ch[i] + a[i]; 14 while (ans[i] > 'z') ans[i] -= 26, ans[i - 1]++; 15 } 16 if (ans[0]) cout << -1; 17 else for (int i = 1; i <= 6; i++) cout << (char)ans[i]; 18 cout << endl; 19 } 20 return 0; 21 }
I、I题是个签到题
1、链接
https://ac.nowcoder.com/acm/contest/3006/I
2、题面
经过2019一年的比赛,牛牛战队的队员发现了一个重大规律:I题是个签到题。
签到题的定义是:通过人数大于等于全场人数的80%或者通过人数是所有题目前三多的题(也就是最多有两个题目通过人数严格比它多)叫做签到题。
2020赛季就要到了,牛牛战队要去验证这个规律了,已知现在每个题的过题情况,看一看I题是不是一个签到题.
3、思路
I题是个签到题。思路略。需要注意的是,并列第三多也是前三多,注意了这一点代码量就多了很多(相对于原来没几句话的代码量),然后发现出题人自己没考虑这点,后来才加上并重测。
4、代码
1 #include <bits/stdc++.h> 2 using namespace std; 3 4 #define MAXN 100005 5 6 int n, m; 7 8 struct t { 9 int o, p; 10 } a[15]; 11 12 struct cmp { 13 bool operator () (t a, t b) { 14 return a.p > b.p; 15 } 16 } x; 17 18 int main() { 19 cin >> n >> m; 20 for (int i = 1; i <= n; i++) cin >> a[i].p, a[i].o = i; 21 int o = a[9].p; 22 if ((double)m / (double)o <= 1.25) cout << "Yes"; 23 else { 24 sort(a + 1, a + n + 1, x); 25 cout << (a[1].o == 9 || a[2].o == 9 || o == a[3].p ? "Yes" : "No"); 26 } 27 return 0; 28 }
J、牛牛战队的秀场
1、链接
https://ac.nowcoder.com/acm/contest/3006/J
2、题面
牛牛战队里,不仅有训练,也有追逐。
牛牛和牛能总是想知道谁更秀一点,他们通常会去比谁的代码更秀,谁的成绩更秀……
这一次,他们开始比谁的走位更秀。他们来到一个半径为r的圆上,画了圆内接的正n边形。为了秀走位,他们只允许自己在多边形的边上移动。
同时,他们随便选取正n边形的一个顶点为1号顶点,按顺时针的顺序把其他的点叫做2号顶点,3号顶点……一开始,两人分别在i号顶点和j号顶点。
现在,牛牛要一边沿着多边形的边秀走位,一边走向牛能。他想知道,他最短要走多少距离才能走到牛能的旁边?。
3、思路
计算几何。n边形的边长l = sin(Pi / n) * 2 * r,再乘上要走的边数。
4、代码
1 #include <bits/stdc++.h> 2 using namespace std; 3 4 #define Pi 3.1415926535 5 6 int n, r, x, y; 7 8 int main() { 9 cin >> n >> r >> x >> y; 10 if (y < x) swap(x, y); 11 printf("%.6lf", min(y - x, n - y + x) * sin(Pi / n) * 2 * r); 12 return 0; 13 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号