[Nowcoder]2020牛客寒假算法基础集训营2
20200206 第二场
进度(10 / 10)
A、做游戏
1、链接
https://ac.nowcoder.com/acm/contest/3003/A
2、题面
牛牛和 牛可乐在玩石头剪刀布。
- 胜负关系如下:

3、思路
小型贪心。牛牛出石头时牛可乐优先出剪刀,同理剪刀-布,布-石头。三次比较均取两者较小值,剩下的便是不可能获胜的局了。
4、代码
1 #include <bits/stdc++.h> 2 using namespace std; 3 4 long long a, b, c, d, e, f; 5 6 int main() { 7 cin >> a >> b >> c >> d >> e >> f; 8 cout << min(a, e) + min(b, f) + min(c, d); 9 return 0; 10 }
B、排数字
1、链接
https://ac.nowcoder.com/acm/contest/3003/B
2、题面
牛可乐 最喜爱的字符串是 616。
牛可乐得到了一个纯数字的字符串 S,他想知道在可以任意打乱 S 顺序的情况下,最多有多少个不同的子串为 616。
当两个子串 S[l1…r1],S[l2…r2] 满足 l1≠l2 或 r1≠r2 时它们被认为是不同的。
3、思路
签到题。将字符串中1和6提取出来,以616161...的形式排列为最优解,则统计1和6的个数并处理一下即可得到答案。
4、代码
1 #include <bits/stdc++.h> 2 using namespace std; 3 4 #define MAXN 200005 5 6 int n, a, b; 7 char s[MAXN]; 8 9 int main() { 10 cin >> n >> s; 11 for (int i = 0; i < n; i++) a += s[i] == '1', b += s[i] == '6'; 12 cout << min(a, b - 1); 13 return 0; 14 }
C、算概率
1、链接
https://ac.nowcoder.com/acm/contest/3003/C
2、题面
牛牛刚刚考完了期末,尽管 牛牛 做答了所有 n 道题目,但他不知道有多少题是正确的。
不过,牛牛 知道第 i 道题的正确率是 pi。
牛牛 想知道这 n 题里恰好有 0,1,…,n 题正确的概率分别是多少,对 10^9+7 取模。
对 10^9+7 取模的含义是:对于一个 b≠0 的不可约分数 a/b,存在 q 使得 b * q mod (10^9+7) =a,q 即为 a / b 对 10^9+7 取模的结果。
3、思路
自己瞎捣鼓了许久没做出来。看了下题解,发现我duck不必纠结于将pi化成分数形式。
这也算是一道DP题。设f[i][j]表示前i道题里j道题正确的概率,状态转移:f[i][j] = f[i - 1][j - 1] * p[i] + f[i - 1][j] * p_[i],其中p_[i]表示做错的概率。
根据题意,p_[i] = mod + 1 - p[i],上述数据全部需要取模。
4、代码
1 #include <bits/stdc++.h> 2 using namespace std; 3 4 typedef long long ll; 5 6 #define MAXN 2005 7 #define MOD 1000000007 8 9 ll n, a[MAXN], b[MAXN], f[MAXN][MAXN]; 10 11 int main() { 12 cin >> n; 13 for (int i = 1; i <= n; i++) 14 cin >> a[i], b[i] = (MOD + 1 - a[i]) % MOD; 15 f[0][0] = 1; 16 for (int i = 1; i <= n; i++) { 17 f[i][0] = (f[i - 1][0] * b[i]) % MOD; 18 for (int j = 1; j <= i; j++) 19 f[i][j] = ((f[i - 1][j] * b[i]) % MOD + (f[i - 1][j - 1] * a[i]) % MOD) % MOD; 20 } 21 for (int i = 0; i <= n; i++) cout << f[n][i] << ' '; 22 return 0; 23 }
D、数三角
1、链接
https://ac.nowcoder.com/acm/contest/3003/D
2、题面
牛牛得到了一个平面,这个平面上有 n 个不重合的点,第 i 个点的坐标为 (xi,yi)。
牛牛想知道,这 n 个点形成的三角形中,总共有多少个钝角三角形。
3、思路
平面几何题。枚举任意两个点,再选择第三个点,看是否满足钝角三角形的条件。设当前选择的两个点为A, B,如图所示,

根据几何知识,当且仅当第三个点位于如下两种位置,可以与A, B组成钝角三角形:
①以AB中点为圆心的圆内;
②不在与AB所连的线段垂直且分别过A, B的两条直线之间(排除①的圆内)。
文字描述显得比较拗口,但图示就比较清晰了。那么:
对于①,求得中点和半径,判定第三个点和圆心距离是否小于半径即可;
对于②,求得直线AB的斜率,进而求得与之垂直的直线的斜率k,分别将A, B, 所求的第三个点代入求得所在直线的截距b,如果第三个点的b小于A的或者大于B的,即满足条件。
平面几何题一个常见的要考虑的问题就是斜率为0或者斜率为无穷大的情况,需要特殊考虑。
4、代码
1 #include <bits/stdc++.h> 2 using namespace std; 3 4 #define MAXN 200005 5 6 int n, ans; 7 double x[MAXN], y[MAXN]; 8 9 double dis(int a, int b) { 10 return sqrt((y[a] - y[b]) * (y[a] - y[b]) + (x[a] - x[b]) * (x[a] - x[b])); 11 } 12 13 int main() { 14 cin >> n; 15 for (int i = 1; i <= n; i++) cin >> x[i] >> y[i]; 16 for (int i = 1; i <= n - 2; i++) 17 for (int j = i + 1; j <= n - 1; j++) { 18 x[0] = (x[j] + x[i]) / 2.0, y[0] = (y[j] + y[i]) / 2.0; 19 double r = dis(i, 0); 20 for (int l = j + 1; l <= n; l++) { 21 if (y[j] == y[i]) 22 ans += (x[l] < min(x[i], x[j]) || x[l] > max(x[i], x[j])) && y[l] != y[i]; 23 else if (x[j] == x[i]) 24 ans += (y[l] < min(y[i], y[j]) || y[l] > max(y[i], y[j])) && x[l] != x[i]; 25 else { 26 double k = -1 / ((y[j] - y[i]) / (x[j] - x[i])); 27 double bi = y[i] - k * x[i], bj = y[j] - k * x[j]; 28 if (-1 / ((y[l] - y[i]) / (x[l] - x[i])) == k) continue; 29 double bl = y[l] - k * x[l]; 30 ans += bl < min(bi, bj) || max(bi, bj) < bl; 31 } 32 ans += dis(l, 0) < r; 33 } 34 } 35 cout << ans; 36 return 0; 37 }
E、做计数
1、链接
https://ac.nowcoder.com/acm/contest/3003/E
2、题面
这一天,牛牛与 牛魔王相遇了――然而这并不在 牛牛期望之中。
牛魔王不出意料又给 牛牛一道看似很难的题目:求有多少个不同的正整数三元组 (i,j,k) 满足 且 i×j≤n。
牛牛并不会做,你能略施援手吗?
当两个三元组 (i1,j1,k1),(i2,j2,k2) 满足 i1≠i2 或 j1≠j2 或 k1≠k2 时它们被认为是不同的。
3、思路
看到根号第一反应是平方。数学符号太难打了,直接复制别人的题解好了。

然后我就一个个i去枚举,,果不其然就T了。想了许久也没找到个好办法,看了题解给的code:
枚举小于n的完全平方数x,再枚举x的因子,仅需在sqrt(x)范围内枚举,由于(i, j)和(j, i)不等价,再在结果上*2即可,当然(i, i)需要特殊考虑。
4、代码
1 #include <bits/stdc++.h> 2 using namespace std; 3 4 int n, ans; 5 6 int main() { 7 cin >> n; 8 for (int i = 1; i <= sqrt(n); i++) { 9 int o = i * i; 10 for (int j = 1; j <= sqrt(o); j++) 11 ans += i == j ? 1 : o % j == 0 ? 2 : 0; 12 } 13 cout << ans; 14 return 0; 15 }
F、拿物品
1、链接
https://ac.nowcoder.com/acm/contest/3003/F
2、题面
牛牛和 牛可乐 面前有 n 个物品,这些物品编号为 1,2,…,n ,每个物品有两个属性 ai,bi 。
牛牛与 牛可乐会轮流从剩下物品中任意拿走一个, 牛牛先选取。
设 牛牛选取的物品编号集合为 H,牛可乐选取的物品编号的集合为 T,取完之后,牛牛 得分为 ∑i∈Hai;而 牛可乐得分为 ∑i∈Tbi。
牛牛和 牛可乐都希望自己的得分尽量比对方大(即最大化自己与对方得分的差)。
你需要求出两人都使用最优策略的情况下,最终分别会选择哪些物品,若有多种答案或输出顺序,输出任意一种。
3、思路
贪心。这题思路不错,值得细品的一种贪心。
由于目的是使得分差最大,对于物品i,A得ai,B得bi,如果A拿了,相当于A得了分,而B同时没得到分,则相当于分差拉开了ai +bi。
根据这个贪心思路,我们将物品按照ai + bi从大到小的顺序排序,然后两人依次拿即可。
4、代码
1 #include <bits/stdc++.h> 2 using namespace std; 3 4 #define MAXN 200005 5 6 int n, ans[2][MAXN], o = 1; 7 8 struct item { 9 int p[3], o; 10 } a[MAXN]; 11 12 struct cmp { 13 bool operator () (item a, item b) { 14 return a.p[2] > b.p[2]; 15 } 16 } x; 17 18 int main() { 19 cin >> n; 20 for (int j = 0; j <= 1; j++) 21 for (int i = 1; i <= n; i++) cin >> a[i].p[j], a[i].o = i; 22 for (int i = 1; i <= n; i++) a[i].p[2] = a[i].p[0] + a[i].p[1]; 23 sort(a + 1, a + n + 1, x); 24 for (int i = 1; i <= n; i++) o ^= 1, ans[o][(i - 1) / 2 + 1] = a[i].o; 25 for (int i = 1; i <= n - n / 2; i++) cout << ans[0][i] << ' '; 26 cout << endl; 27 for (int i = 1; i <= n / 2; i++) cout << ans[1][i] << ' '; 28 return 0; 29 }
G、判正误
1、链接
https://ac.nowcoder.com/acm/contest/3003/G
2、题面
牛可乐有七个整数 a,b,c,d,e,f,g 并且他猜想 a^d+b^e+c^f=g。但牛可乐无法进行如此庞大的计算。
请验证牛可乐的猜想是否成立。
3、思路
这么憨批的签到题我还去推式子。。想着应该没这么简单。
然后写个快速幂又被卡常@!%@#¥#
可以直接用pow,可以写快速幂,快速幂模数设成1e9+7可过,列一下常用模数方便以后用:
12255871, 16341163, 21788233, 29050993, 38734667, 51646229, 68861641, 91815541, 1000000007, 1000000009
4、代码
1 #include <bits/stdc++.h> 2 using namespace std; 3 4 typedef long long ll; 5 #define MOD 1000000007 6 7 ll t, a, b, c, d, e, f, g; 8 9 ll qpow(ll x, ll y) { 10 ll o = x, res = 1; 11 while (y) { 12 if (y & 1) (res *= o) %= MOD; 13 (o *= o) %= MOD, y >>= 1; 14 } 15 return res; 16 } 17 18 int main() { 19 cin >> t; 20 for (int i = 1; i <= t; i++) { 21 cin >> a >> b >> c >> d >> e >> f >> g; 22 printf(qpow(a, d) + qpow(b, e) + qpow(c, f) == g ? "Yes\n" : "No\n"); 23 } 24 return 0; 25 }
H、施魔法
1、链接
https://ac.nowcoder.com/acm/contest/3003/H
2、题面
牛可乐有 n 个元素( 编号 1..n ),第 i 个元素的能量值为 ai。
牛可乐可以选择至少 k 个元素来施放一次魔法,魔法消耗的魔力是这些元素能量值的极差。形式化地,若所用元素编号集合为 S,则消耗的魔力为 maxi∈S{ai}−mini∈S{ai}。
牛可乐要求每个元素必须被使用恰好一次。
牛可乐想知道他最少需要多少魔力才能用完所有元素,请你告诉他。
3、思路
大概知道是个DP,但思路有问题,总是困扰于O(n ^ 2)的算法。
首先元素顺序无关,可以将其从小到大排序。f[i]表示前 i 个元素全部使用一次,最少需要的魔力。
考虑到对于第 i 个元素,可以与第i - 1个元素所在的那次魔法组合,即f[i] = f[i - 1] + (a[i] - a[i - 1]);也可以作为一个魔法的第 k 大元素,即f[i] = f[i - k] + (a[i] - a[i - k + 1]),两者取最小值即可。
另外,前 k 个元素必然组成一个魔法,所以先预处理出来:f[k] = a[k] - a[1]。
4、代码
1 #include <bits/stdc++.h> 2 using namespace std; 3 4 #define MAXN 300005 5 #define INF 0x3f3f3f3f 6 7 int f[MAXN], a[MAXN], n, k; 8 9 int main() { 10 cin >> n >> k; 11 memset(f, INF, sizeof(f)); 12 for (int i = 1; i <= n; i++) cin >> a[i]; 13 sort(a + 1, a + n + 1); 14 f[k] = a[k] - a[1]; 15 for (int i = k + 1; i <= n; i++) 16 f[i] = min(f[i - 1] - a[i - 1] + a[i], f[i - k] - a[i - k + 1] + a[i]); 17 cout << f[n]; 18 }
I、施魔法
1、链接
https://ac.nowcoder.com/acm/contest/3003/I
2、题面
在无垠的宇宙中,有 n 个星球,第 i 个星球有权值 vi。
由于星球之间距离极远,因此想在有限的时间内在星际间旅行,就必须要在星球间建立传送通道。
任意两个星球之间均可以建立传送通道,不过花费并不一样。第 i 个星球与第 j 个星球的之间建立传送通道的花费是 lowbit(vi⊕vj),其中 ⊕ 为二进制异或,而 lowbit(x) 为 x 二进制最低位 1 对应的值,例如 lowbit(5)=1,lowbit(8)=8。特殊地,lowbit(0)=0。
牛牛想在这 n 个星球间穿梭,于是――你需要告诉 牛牛,要使这 n 个星球相互可达,需要的花费最少是多少。
3、思路
题解思路非常巧妙,我很喜欢,就是解释的太草率了,看半天没看懂。
题目把花费定义为二进制相关,看起来很麻烦,其实提炼出来很简单——从二进制最低位找起,如果存在第 k 位,使得既存在该位为0的权值又存在该位为1的权值,如图所示: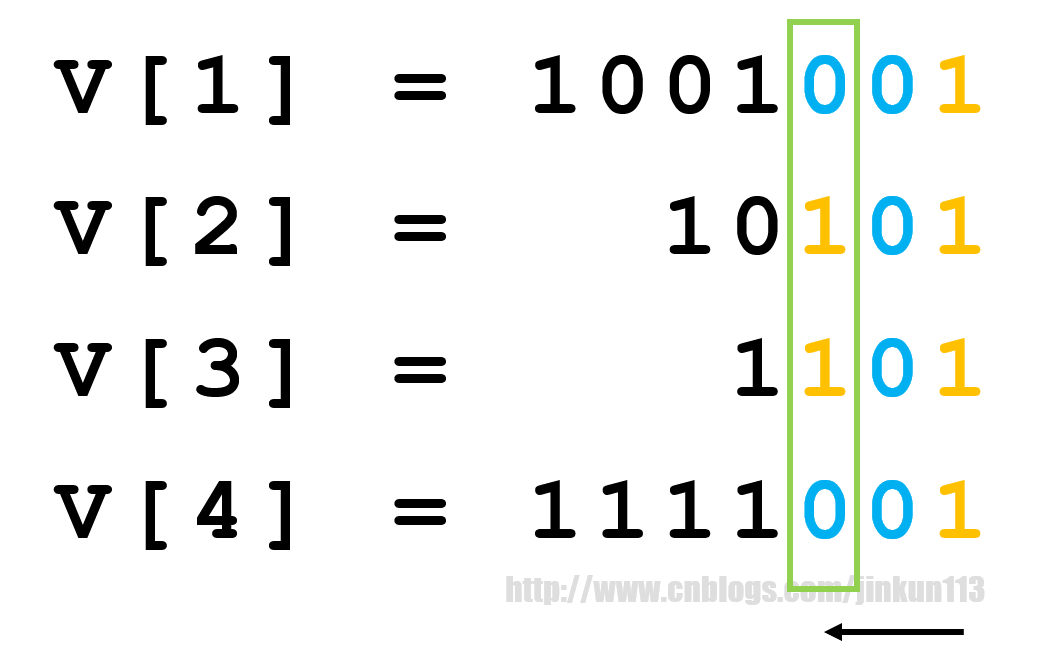
由于只需让n个点连通即可,即连接n - 1条线。第 k 位前的二进制位对于所有权值全部相同,不再需要考虑;第 k 位分为 0 和 1 两种情况,如图所示,我们将它们分成两部分,并分别选出一个点作为代表,对于每一个该位为 0 的点和代表该位为 1 的点相连,对于每一个该位为 1 的点和代表该位为 0 的点相连,总共连接了 n 次,由于两个代表之间连接了两次,删去一次,即n - 1次。而每一次连接,代价均为lowbit() = 2 ^ k,故总代价为 (n - 1) * 2 ^ k。(右图移动了点的位置,以方便看清结构)

不过做到这里还有一个细节没有考虑——如果存在两个点权值相同,即相连代价为0,则可以得到更优解。如图所示,如果存在这样2对相同权值的点,则可以少连2条代价为2 ^ k的线,所以我们可以先对所有权值排序并统计出相同权值的节点对数个数m,最后的总代价为 (n - m - 1) * 2 ^ k。

最后对代码进行一些解释:
为得到上述的第 k 位,我们定义两个变量:x表示对权值连续取和,y表示对权值连续取或。根据二进制相关知识,当且仅当某一位存在1,连续取和结果为1;当且仅当某一位存在0,连续取或结果为0;再将 x 异或 y,所得结果如果某一位为1,表示x该位为1,y为0,再从最低位枚举,可得第 k 位。
4、代码
1 #include <bits/stdc++.h> 2 using namespace std; 3 4 #define MAXN 200005 5 #define INF 0x7fffffff 6 7 int n, x = INF, y, v[MAXN], m, ans; 8 9 int main() { 10 cin >> n; 11 for (int i = 1; i <= n; i++) { 12 cin >> v[i]; 13 x &= v[i], y |= v[i]; 14 } 15 x ^= y; 16 sort(v + 1, v + n + 1); 17 for (int i = 1; i <= n - 1; i++) 18 m += v[i] == v[i + 1]; 19 for (int i = 0, o = 1; i <= 30; i++, o <<= 1) 20 if (x & o) { 21 ans = (n - m - 1) * o; 22 break; 23 } 24 cout << ans; 25 return 0; 26 }
(有个迷惑的地方是,我开始是直接输出的,即 cout << (n - m - 1) * o; 死活有一个点过不了,是什么原因?)
破案了,因为可能出现没结果的情况,然后默认输出0就能过(这是题目的锅⑧
J、求函数
1、链接
https://ac.nowcoder.com/acm/contest/3003/J
2、题面
牛可乐有 n 个一次函数,第 i 个函数为 fi(x)=ki*x+bi。
牛可乐有 m 次操作,每次操作为以下二者其一:
• 1 i k b 将 fi(x)修改为 fi(x)=k*x+b。
• 2 l r 求 fr(fr−1(⋯(fl+1(fl(1)))⋯ ))。
牛可乐当然(bu)会做啦,他想考考你——
答案对 10^9+7 取模。
3、思路
一道不错的线段树题。
代码中Tree结构体
4、代码
1 #include <bits/stdc++.h> 2 using namespace std; 3 4 #define MAXN 200005 5 #define MOD 1000000007 6 7 #define ls o << 1 8 #define rs o << 1 | 1 9 10 typedef long long ll; 11 12 ll n, m, k[MAXN], b[MAXN]; 13 ll ox, ok, ob, ql, qr, p; 14 15 struct Tree { 16 ll x, y; 17 Tree() {} 18 Tree(ll _x, ll _y) { x = _x, y = _y; } 19 } t[MAXN << 2]; 20 21 void build(int o, int l, int r) { 22 if (l == r) { 23 t[o] = Tree(k[l], b[l]); 24 return; 25 } 26 int m = (l + r) >> 1; 27 build(ls, l, m), build(rs, m + 1, r); 28 t[o] = Tree(t[ls].x * t[rs].x % MOD, (t[ls].y * t[rs].x + t[rs].y) % MOD); 29 } 30 31 void upd(int o, int l, int r) { 32 if (l == r) { 33 t[o] = Tree(ok, ob); 34 return; 35 } 36 int m = (l + r) >> 1; 37 if (ox <= m) upd(ls, l, m); 38 else upd(rs, m + 1, r); 39 t[o] = Tree(t[ls].x * t[rs].x % MOD, (t[ls].y * t[rs].x + t[rs].y) % MOD); 40 } 41 42 Tree query(int o, int l, int r) { 43 Tree rl, rr; 44 if (ql <= l && r <= qr) return Tree(t[o].x, t[o].y); 45 int m = (l + r) >> 1, fl = 0, fr = 0; 46 if (ql <= m) rl = query(ls, l, m), fl = 1; 47 if (qr > m) rr = query(rs, m + 1, r), fr = 1; 48 return fl && fr ? Tree(rl.x * rr.x % MOD, (rl.y * rr.x + rr.y) % MOD) : fl ? rl : rr; 49 } 50 51 int main() { 52 cin >> n >> m; 53 for (int i = 1; i <= n; i++) cin >> k[i]; 54 for (int i = 1; i <= n; i++) cin >> b[i]; 55 build(1, 1, n); 56 for (int i = 1; i <= m; i++) { 57 cin >> p; 58 if (p == 1) { 59 cin >> ox >> ok >> ob; 60 upd(1, 1, n); 61 } 62 else { 63 cin >> ql >> qr; 64 Tree ans = query(1, 1, n); 65 cout << (ans.x + ans.y) % MOD << endl; 66 } 67 } 68 return 0; 69 }
疑惑:第一次交了然后TLE了,调了半天,还去和标程对比了老半天,然后再交一发一模一样的告诉我A了?黑人问号.jpg



