递归与分治策略基础练习笔记
递归方法就是自己调用自己的方法,自己调用自己会导致反复调用同一方法,必须用if和return设置一个结束语句才能停下来。这和循环非常相似,下面举一些例子探讨一下两者的区别。
【例1】计算n的阶乘。
递归公式:0! = 1,n! = n*(n-1)。非递归公式:0! = 1,n!=1×2×3×...×(n-1)×n。

1 /**递归求一个非负整数的阶乘
2 * @param n 非负整数
3 * @return n的阶乘
4 * T(n)=O(n), S(n)=O(n)
5 */
6 private static long factorial1(int n){
7 if (n<=1){
8 return 1;
9 }
10 return n * factorial1(n-1);
11 }
12 /**循环求一个非负整数的阶乘
13 * @param n 非负整数
14 * @return n的阶乘
15 * T(n)=O(n), S(n)=O(1)
16 */
17 private static long factorial2(int n){
18 //记录第i次循环的计算结果
19 int fi = 1;
20 for (int i = 1; i <= n; i++) {
21 fi*=i;
22 }
23 return fi;
24 }
递归的时间复杂度T(n)=递归次数×每次递归的时间复杂度。计算n!的递归方法每次递归计算一次乘法T(n)=O(1),递归了n次,所以T(n)=O(n)。因为每次递归方法都依赖它所调用的递归方法的返回值,所以每次递归都要在栈中创建一个新的递归方法,递归算法的空间复杂度S(n)=O(n)。
循环的时间复杂度是循环次数*循环内代码的时间复杂度,所以T(n)=O(n)。因为循环依靠循环体外的变量等存储计算结果,每次循环结束后就被下一次循环覆盖了,所以循环的空间复杂度总是O(1)。
仔细观察发现每次递归之间可以通过小括号内的参数和return语句传递数据,而每次循环之间只能通过外部的变量等传递数据,这个递归也可以。循环的小括号的功能不太实用,因为if+break结束循环适用范围更广。由此可见循环能做到的事递归也一定能做到,但递归能做到的事循环不一定能做到。
在这道题中,先用小括号传递数据再用return返回数据的过程显然是冗长低效的。优化方法是把每次递归中计算的结果放到小括号中传给下一次递归,最后一次递归时直接返回给调用递归的main方法,这样就可以避免一个冗长的返回过程,这样的递归称为尾递归,当编译器检测到这是一个尾递归时,判断出下一次递归不被调用它的递归方法依赖,下一次递归就会覆盖当前的递归方法而不是在栈中创建一个新的。所以尾递归的空间复杂度为S(n)=O(1)。尾递归和循环更相似。

1 /**尾递归求一个非负整数的阶乘
2 * @param n 非负整数
3 * @param fi 记录第i次递归的计算结果,初始为1
4 * @return n的阶乘
5 * T(n)=O(n), S(n)=O(1)
6 */
7 private static long factorial3(int n, int fi){
8 if (n<=1){
9 return fi;
10 }
11 return factorial3(n-1,fi*n);
12 }
【例2】计算斐波那契数列的第n项。斐波那契数列:1,1,2,3,5,8,13,21,34,55,89,144……
直接套公式,递归表达式:F(1)=1,F(2)=1,F(n)=F(n - 1)+F(n - 2),(n ≥ 3,n ∈ N*);

1 /**递归求斐波那契数列第 n项
2 * @param n
3 * @return
4 * T(n)=O(2^n),S(n)=O(2^n)
5 */
6 private static long fibonacci1(int n){
7 //n>92时,f(n)的值大于long的范围
8 if (n<3||n>92){
9 return 1;
10 }
11 return fibonacci1(n-1)+fibonacci1(n-2);
12 }
递归的算法可读性最强,但效率也最低。每次递归都调用了自身两次,计算第n项递归了2^n次,T(n)=O(2^n)。因为每个递归方法都依赖它所调用的递归方法的返回值,所以每次递归都要在栈中创建一个新方法,S(n)=O(2^n)。
显然,递归算法中有很多子问题被重复计算了。优化的方法是改递归为递推,因为每一项的计算只依赖前两项,可以设两个变量记录连续两项的值,然后不断递推下一项,计算第n项递推了n次,且占用空间不变,循环法和尾递归法都是如此,T(n)=O(n),S(n)=O(1)。

1 /**循环求斐波那契数列第 n项
2 * @param n
3 * @return
4 * T(n)=O(n),S(n)=O(1)
5 */
6 private static long fibonacci2(int n){
7 if (n<3||n>92){
8 return 1;
9 }
10 /*f1,f2记录数列连续的两项的值,每次循环递推地
11 更新f1,f2,比如由1,2项更新到2,3项,循环结束后
12 f1,f2等于第n-1,n项值,temp帮助更新f1,f2.*/
13 long f1 = 1, f2 = 1, temp;
14 for (int i = 3; i <= n; i++) {
15 temp = f1;
16 f1 = f2;
17 f2 += temp;
18 }
19 return f2;
20 }
21
22 /**尾递归求斐波那契数列第 n项
23 * @param n
24 * @param f1 f1,f2记录数列连续的两项的值,初始值都为1
25 * @param f2 每次递归f1,f2都更新为其后一项的值
26 * @return 递归结束后f1,f2等于第n-1,n项值,返回f2
27 * T(n)=O(n),S(n)=O(1)
28 */
29 private static long fibonacci3(int n,long f1,long f2){
30 if (n<3||n>92){
31 return f2;
32 }
33 return fibonacci3(n-1,f2,f1+f2);
34 }
【例3】设计阿克曼函数的算法,阿克曼函数(Ackermann)是非原始递归函数,不能用非递归的方式定义。阿克曼函数的一个变量调用了递归函数,所以它还是一个双递归函数。它的定义如下:
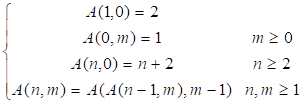
当m=0时,A(n,m)=A(n,0)=n+2。把m=0看成一个常量,A(n,0)=n+2就是一个单递归函数。
当m=1时,因为A(1,1)=A(A(0,1),0)=A(1,0)=2,A(n,1)=A(A(n-1,1)0)=A(n-1,1)+2=2n,所以A(n,1)=2n是一个单递归函数。
当m=2时,因为A(1,2)=A(A(0,2),1)=A(1,1)=2,A(n,2)=A(A(n-1,2),1)=2A(n-1,2)=2^n,所以A(N,2)=2^n是一个单递归函数。
当m=3时,因为A(1,3)=A(A(0,3),2)=A(1,2)=2,A(n,3)=A(A(n-1,3),2)=2^A(n-1,3)=2^A(A(n-2,3),2)=2^2^A(n-2,3),A(n,3)=2^2^…^2(n层2次幂)也是一个单递归函数。
A(n,4)的增长速度太快,A(3,4)就已经大得无法准确计算,所以无法表示。
观察上面的分析可以发现,双递归函数A(n,m)就是由A(n,0),A(n,1),A(n,2)…组成的单递归函数序列,m可以看作这个序列的下标,调用A(n,m)时输入不同的下标可以调用不同的单递归函数实现不同的功能。
算法直接套公式,要考的话应该是给几个参数手动算算。
【例4】输入一个正整数 N,求这个数的各位数字之和。
先把N对10求余得出个位数,然后把N减去个位数再除以十,使十位变成个位,再调用本方法计算并累加,当N=0时结束递归。

1 /**递归求正整数n的各位数和
2 * @param n
3 * @return
4 *T(n)=O(logn),S(n)=O(logn)
5 */
6 private static int f1(int n){
7 if (n <= 0) {
8 return 0;
9 }
10 return n%10 + f1((n - n%10)/10);
11 }
12
13 /**尾递归求正整数n的各位数和
14 * @param n
15 * @param sum 记录每次递归的计算结果,初始为0
16 * @return
17 * T(n)=O(logn),S(n)=O(1)
18 */
19 private static int f2(int n, int sum){
20 if (n <= 0) {
21 return sum;
22 }
23 return f2((n - n%10)/10,sum+n%10);
24 }
25
26 /**循环求正整数n的各位数和
27 * @param n
28 * @return
29 * T(n)=O(logn),S(n)=O(1)
30 */
31 private static int f3(int n){
32 int sum = 0;
33 while (n > 0) {
34 sum += n % 10;
35 n = (n - n%10)/10;
36 }
37 return sum;
38 }
39 /*时间复杂度分析:设n=100,n=10²,logn=2,要递归logn +1次,每次递归计算两个数,T(n)=O(2)=O(1),总的T(n)=logn,空间复杂度线性递归的S(n)=T(n),循环和尾递归的S(n)=O(1)。*/
【例5】给定一个长度为 k 的序列 A = {a1, a2, ..., ak},以及变量 x (1 ≤ x ≤ k),要求给出所有的 x-元组。比如 A = {a1, a2, a3},当 x = 1 时,则所有的 1 元组集为 {(a1), (a2), (a3)};当 x = 2 时,则所有的 2 元组集为 {(a1, a2), (a1, a3), (a2, a3)};当 x = 3 时,则所有的 3 元组集为 {(a1, a2, a3)}。
这题就是求k取x的组合,把x为所有值时的组合分别求出来加起来就是答案啦。组合公式如下,本题n=k,m=x。

可以先根据阶乘公式设一个求阶乘的方法,再设一个求组合的方法调用阶乘方法计算组合公式,再设一个方法循环k次获得x的k个值并分别调用求组合方法求k取x的组合数,然后累加当前x值时的组合数,最后循环完就可得答案。

1 /**循环求一个非负整数的阶乘
2 * @param n 非负整数
3 * @return n的阶乘
4 * T(n)=O(n), S(n)=O(1)
5 */
6 private static long factorial(int n){
7 //记录第i次循环的计算结果
8 int fi = 1;
9 for (int i = 1; i <= n; i++) {
10 fi*=i;
11 }
12 return fi;
13 }
14 /**求组合
15 * @param m
16 * @param n
17 * @return
18 */
19 private static int combination(int m, int n){
20 if (n==0) {
21 return 0;
22 }
23 if(n==m||n==1||m==0) {
24 return 1;
25 }
26 if (n<m) {
27 return combination(n,n);
28 }
29 //以上都是组合的数学规律
30 if (m==1) {
31 return n;
32 }
33 //套公式
34 return factorial(n)/(factorial(m)*factorial(n-m));
35 }
36
37 /**求x为所有值的组合数之和
38 * @param k
39 * @return
40 */
41 public static int cx(int k){
42 int a=0;
43 for (int x = 1; x <= k ; x++) {
44 a+=combination(x,k);
45 }
46 return a;
47 }
【例6】楼梯有 N 阶台阶,上楼可以一步上1阶,也可以一步上2阶,编一程序计算共有多少种不同的走法。
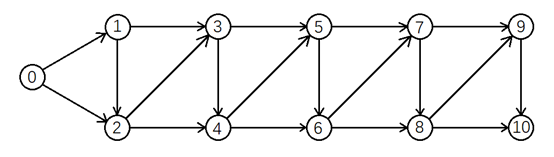
画个图就很容易发现从第三台阶开始,每个台阶都可以从前一台阶走一步到达,或者从前二台阶走两步到达,所以走法等于前两个台阶走法数之和。这就是斐波那契数列,不重复了。
【例7】(汉诺塔问题)有三根相邻的柱子,标号为A,B,C,A柱子上从下到上按金字塔状叠放着n个不同大小的圆盘,要把所有盘子一个一个移动到柱子C上,并且每次移动同一根柱子上都不能出现大盘子在小盘子上方,请问至少需要多少次移动,设移动次数为H(n)。
首先把上面的n-1个圆盘经过C移动到B柱,移动了H(n-1)次,然后把最下面的圆盘移动到C柱,再把B柱的n-1个圆盘经过A移动到C柱,移动了H(n-1)次,总共移动了2*H(n-1)+1次。由此得到H(n)的递归表达式:
H(n)=1 (n=1)
H(n)= 2*H(n-1)+1 (n>1)
化成一般式:
H(n) = 2^n - 1 (n>0)

1 /**递归法求汉诺塔移动次数
2 * @param n 盘数
3 * @return
4 * T(n)=O(2^n),S(n)=O(2^n)
5 */
6 private static int hanoi1(int n){
7 if (n == 1) {
8 return 1;
9 } else {
10 return 2*hanoi1(n-1)+1;
11 }
12 }
13
14 /**非递归法求汉诺塔移动次数
15 * @param n 盘数
16 * @return
17 * T(n)=O(2^n),S(n)=O(1)
18 */
19 private static int hanoi2(int n){
20 return 2^n-1;
21 }
22
23 /**递归法求汉诺塔移动次数并打印移动步骤
24 * @param n 盘数
25 * @param a 柱子代号
26 * @param b
27 * @param c
28 *T(n)=O(2^n),S(n)=O(1)
29 */
30 private static void hanoi3(int n, char a, char b, char c) {
31 if (n == 1) {
32 System.out.println("move:" + a + "--->" + c);
33 } else {
34 //先递归地将上面的n-1个盘子由a经过c移动到b
35 hanoi3(n - 1, a, c, b);
36 //再移动剩下的一个盘子从a到c,并打印这个步骤
37 System.out.println("move:" + a + "--->" + c);
38 //最后递归地将上面的n-1个盘子由b经过a移动到c
39 hanoi3(n - 1, b, a, c);
40 }
41 }
【例8】整数划分问题:给定一个正整数 x,用一系列正整数之和表示,即 x = x1 + x2 + ... + xk,其中 x1 ≥ x2 ≥ ... ≥ xk。求不同划分方法的数目 f(x)。比如 x = 5:5 = 5;5 = 4 + 1;5 = 3 + 2;5 = 3 + 1 + 1;5 = 2 + 2 + 1;5 = 2 + 1 + 1 + 1;5 = 1 + 1 + 1 + 1 + 1。
n和f(n)之间没有明确的函数关系,所以只能根据已知的关系设置一些条件限制,每当符合某种条件时方法数就加一,然后改变参数值继续递归,直到符合某个条件结束递归,返回累计的方法数。
为了方便统计,增加一个变量m把所有划分数分成两部分,将最大加数n1≤m的划分方法个数记作f(n,m),当n=m时,f(n)=f(n,m),即f(n)=f(n,n)。当n=1或m=1时都只有一种划分方法。当n<m时,按m的定义可知划分方法数等于f(n,n)。当n=m时,已知n1=n时划分方法只有一种,因此划分方法数累加一,剩下的n1<m的划分方法记作f(n,m-1)种。当n>m>1时, 分两种情况, n1=m时,划分公式可化为n-n1=n2+n3+…+nk;把n-n1当作新的n,n2当作新n1,因为n-n1=m,n2≤n1=m,所以n1=m时的方法数记作f(n-m,m);n1<m时,按m的定义可知划分方法数等于f(n,m-1)种;所以n≥m时的划分方法数记作f(n-m,m)+f(n,m-1)。综上可得f(n)的递归表达式:
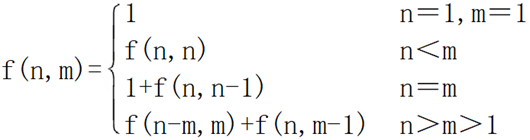

1 /**整数划分问题
2 * @param n
3 * @param m
4 * @return
5 * T(n)=O(n^2),S(n)=O(n^2)
6 */
7 private static int f(int n, int m){
8 //传入的数据不合法
9 if(n < 0 || m < 0) {
10 return 0;
11 }
12 /*因为n=1或m=1都只有一种情况,
13 所以将此作为终止递归的条件*/
14 if (n == 1 || m == 1) {
15 return 1;
16 }
17 if (n < m) {
18 return f(n,n);
19 }
20 if (n == m) {
21 return (1+ f(n,m-1));
22 }
23 return f(n,m-1)+ f(n-m,m);
24 }
25 /*复杂度分析:f(n,n)的T(n)=O(1),1+f(n,n-1)递归n次,每次计算一个加法,总的T(n)=O(n),f(n-m,m)+f(n,m-1)递归n+m次,每次计算一个加法,总的T(n)=O(2n)=O(n),每次只能执行其中一个递归式,所以T(n)=O(1)*O(n)*O(n)=O(n^2),因为是线性递归,S(n)=T(n)=O(n^2)*/
【例9】给定一列数 A = {a1, a2, ..., an},给出这列数的全部排列。
全排列种数为n!,先用for循环n次,分别把n个元素放到开头,获得n种排列,每次循环中确定第一个元素后再调用自己,for循环n-1次分别把n-1个元素放到第二,获得n×(n-1)种排列,确定第一第二后再调用自己,直到第n-1个元素确定获得n!种排列,然后打印出来。

1 /** 输入一个数组,求该数组所有元素的全排列
2 * @param a 数组
3 * @param index 当前要确定的元素的数组下标,从0开始。
4 * @param length 数组长度
5 * T(n)=O(n!),S(n)=O(n)
6 */
7 private static void fullPermutation(int[] a, int index, int length){
8 /*如果当前下标到达数组最后一个元素,则打印当前数组,结束本次递归。
9 因为第一次调用本方法获得n种排列,第二次调用获得n×(n-1)种,
10 最后一次才是获得n!种,所以在最后一次打印才不会重复。*/
11 if(index>=length-1){
12 System.out.println(Arrays.toString(a));
13 } else{
14 for(int i = index;i<length;i++){
15 //交换元素位置
16 swap(a,index,i);
17 //每次递归下标+1
18 fullPermutation(a,index+1,length);
19 /*复原为下次循环做准备,每次循环只确定一个元素,
20 其他不变才不会出现重复。*/
21 swap(a,index,i);
22 }
23 }
24 }
25
26 /** 数组元素交换方法
27 * @param a 数组
28 * @param i 交换元素1
29 * @param j 交换元素2
30 * T(n)=O(1),S(n)=O(1)
31 */
32 private static void swap(int[] a, int i, int j){
33 int temp = a[i];
34 a[i] = a[j];
35 a[j] = temp;
36 }
37 /*这题用的算法表面上是递归,其实是回溯法。复杂度分析:设数组长度为n,每次递归执行一个循环,循环次数=当前数组长度,每次循环调用一次递归,每次递归n-1,递归中的循环次数也-1,所以递归次数=n×(n-1)×…×1,每次递归中的其他语句都是O(1),所以总的T(n)=O(n!)。每次循环中的递归结束再进行下一次循环,每次递归n-1,最多递归n次,所以S(n)=O(n)。*/
分治策略是把一个规模较大的问题,分解为多个规模较小的子问题,这些子问题互相独立且与原问题形式相同,递归地求解这些子问题,直到规模小到容易解决就直接解决,然后将各子问题的解合并得到原问题的解。
分治策略具有特定的使用范围:
子问题到一定规模很容易解决;
可划分为同质子问题(即最优子结构);
子问题解可合并;
子问题相互独立;
【例1】二分搜索法:给定已按升序排好序长度为m的数组a[],要在a[]中找出一特定元素 x。
用分治策略把数组从中间分成两个子数组,每次分解数组后先把原数组中间元素对比要找的元素x,相等就找到了。因为数组已经升序排列,如果x大于中间元素就说明x在右边的数组中,x小就在左边数组中,另一个数组就不用搜索了。对子数组继续递归,直到子数组只有一个元素就能直接确定x。

1 /**二分搜索
2 * @param a 要搜索的数组
3 * @param x 要搜索的元素
4 * @param min x的搜索范围的上界下标
5 * @param max x的搜索范围的下界下标
6 * @return x在a中的下标
7 * T(n)=O(logn),S(n)=O(1)
8 */
9 private static int binarySearch(int[] a,int x, int min, int max) {
10 /* 计算当前数组的下标中位数,结果有小数自动忽略。其实不用真的分解数组,只要修改x的搜索范围的下标就可以了*/
11 int mid = (min + max ) / 2;
12 //x小于当前的中间元素,则上界改成中间元素下标减一
13 if (x < a[mid]) {
14 return binarySearch(a, x, min, mid - 1);
15 }
16 //x大于当前的中间元素,则下界改成中间元素下标加一
17 if (x > a[mid]) {
18 return binarySearch(a, x,mid + 1, max);
19 }
20 //x等于当前的中间元素,则返回中间元素下标
21 return mid;
22 }
23 /*复杂度分析:设数组长度为n,每次递归n除以2,直到n=1递归了log2n次,T(n)=O(logn),因为是尾递归,S(n)=O(1)。*/
【例2】合并(归并)排序。
用分治策略把数组(数列)从中间分成两个子数组,递归直至每个子序列只有一个元素(单元素序列必有序),再把有序的子序列两两合成有序的新序列,直到所有子序列合并成原序列就完成了排序。一对(每次递归分成的两个)有序序列合并的方法是:先把两个数组的首元素,小的那个取出来放入新数组a,再比首元素,再把小的取出放入a,直到对比的两数组元素取完,新数组a就是合并的有序序列。比如序列8465,二分两次变成8,4,6,5。8和4是一对,合并得48,6和5合并得56,48和56合并,4和5对比取4放入新数组,5和8对比取5,6和8对比取6,剩下的8直接放入新数组,新数组为合并的有序序列4568。

1 /*伪代码:
2 归并排序{
3 输入待排序数组a,辅助数组b,a的首尾下标min和max
4 如果子数组已经最小,结束递归
5 计算a的中间下标mid
6 递归左边子数组输入(a,min,mid)
7 递归右边子数组输入(a,mid+1,max)
8 合并左右子数组输入(a,b,min,mid,max)
9 }
10 合并子数组{
11 输入a,b,min,mid,max
12 左子数组首下标min,尾下标mid
13 右子数组首下标mid+1,尾下标max
14 while(左子数组或右子数组长度不为0){
15 if(左子数组长度为0){
16 取右子数组的首元素放入b数组
17 }elseif(右子数组长度为0){
18 取左子数组的首元素放入b数组
19 }elseif(右子数组首元素大于左子数组首元素){
20 取右子数组的首元素放入b数组
21 }else{
22 取左子数组的首元素放入b数组
23 }
24 }
25 把辅助数组b复制到原数组a
26 }
27 */
28
29 /**归并排序递归算法
30 * @param originalArray 原数组
31 * @param tempArray 辅助合并的数组,要求输入一个和原数组等长的空数组
32 * @param minIndex 当前(子)数组的首下标
33 * @param maxIndex 当前(子)数组的尾下标
34 * T(n)=O(nlogn),S(n)=O(n)
35 */
36 private static void mergeSort(int[] originalArray,int[] tempArray, int minIndex ,int maxIndex) {
37 //子数组已经最小,结束递归
38 if (minIndex>=maxIndex) {
39 return;
40 }
41 //求当前(子)数组的中间下标值
42 int midIndex = (minIndex+maxIndex)/2;
43 //左半部分递归排序
44 mergeSort(originalArray, tempArray, minIndex,midIndex);
45 //右半部分递归排序
46 mergeSort(originalArray, tempArray, midIndex+1,maxIndex);
47 //将左半部分和右半部分合并
48 mergeArrays(originalArray,tempArray,minIndex,midIndex,maxIndex);
49 }
50 /**
51 * @param originalArray 原数组
52 * @param tempArray 辅助合并的数组
53 * @param minIndex 当前(子)数组的首下标
54 * @param midIndex 当前(子)数组的中下标
55 * @param maxIndex 当前(子)数组的尾下标
56 * T(n)=O(n),S(n)=O(1)
57 */
58 private static void mergeArrays(int[] originalArray, int[] tempArray, int minIndex, int midIndex, int maxIndex) {
59 //辅助数组的首下标
60 int tempMin = minIndex;
61 //左子数组的首下标
62 int leftMin = minIndex;
63 //右子数组的首下标
64 int rightMin = midIndex + 1 ;
65 //如果当前子数组只有一个元素则不能合并。
66 if (leftMin >= rightMin ) {
67 return;
68 }
69 //循环条件是左右子数组长度都不为0
70 while (leftMin != midIndex + 1 || rightMin != maxIndex + 1){
71 if (leftMin == midIndex + 1){
72 //如果左子数组长度为0,把右子数组顺序放入辅助数组,下标自增表示当前元素已被取出。
73 tempArray[tempMin++] = originalArray[rightMin++];
74 }else if (rightMin == maxIndex + 1){
75 //如果右子数组长度为0,把左子数组顺序放入辅助数组
76 tempArray[tempMin++] = originalArray[leftMin++];
77 }else if (originalArray[leftMin ] <= originalArray[rightMin ]){
78 //如果右子数组首元素>左子数组首元素,把右子数组首元素放入辅助数组
79 tempArray[tempMin++] = originalArray[leftMin++];
80 }else {
81 //否则把左子数组首元素放入辅助数组
82 tempArray[tempMin++] = originalArray[rightMin++];
83 }
84 }
85 //当原数组的所有元素都按顺序放入辅助数组后,将辅助数组复制到原数组
86 System.arraycopy(tempArray, 0, originalArray, 0, maxIndex + 1);
87 }
【例3】快速排序。
首先选取一个元素作为基准值,把小于基准值的元素划分到左边作为左子数组,大于基准值的元素划分到右边作为右子数组。再递归左右子数组,直到子数组长度等于1。

1 /*伪代码:
2 快速排序{
3 输入待排序数组a,a的首尾下标min和max
4 取出a[min]设为基准
5 if(子数组长度大于2){
6 while(数组元素没搜索完)
7 从尾部往前搜索找到一个小于基准的元素a[x],放到左子数组的空位a[min]
8 从头部往后搜索找到一个大于基准的元素a[y],放到右子数组的空位a[x]
9 }
10 左右子数组划分完后中间剩下一个空位,把基准放进去。
11 递归左子数组
12 递归右子数组
13 }
14 */
15
16 /**快速排序递归算法
17 * @param a 原数组
18 * @param min 当前(子)数组的首下标
19 * @param max 当前(子)数组的尾下标
20 * T(n)=O(nlogn)平均 O(n^2)最坏 ,S(n)=O(logn)平均 O(n)最坏
21 */
22 private static void quickSort(int[] a, int min, int max){
23 //左右两部分的开始下标
24 int i = min, j = max;
25 //取出基准值
26 int pivot = a[i];
27 //子数组长度大于2
28 if(i < j){
29 while (i != j) {
30 //从尾部往前搜索小于基准值的元素a[j]
31 while(j > i && a[j] > pivot) {
32 -- j;
33 }
34 //此时a[i]的值已被pivot记录,相当于空的,可以把a[j]复制过去。
35 a[i] = a[j];
36 //从头部往后搜索大于基准值的元素a[i]
37 while(i < j && a[i] < pivot) {
38 ++ i;
39 }
40 //此时a[j]刚被复制过,相当于空的,可以把新的a[i]复制过去。
41 a[j] = a[i];
42 //这个过程中总有一个元素相当于空值,利用这个空值可以不借助其他变量完成元素的交换
43 }
44 //i=j时划分完当前数组,a[i]在两个子数组的中间且是“空值”。
45 a[i] = pivot;
46 //递归左边子数组
47 quickSort(a, min, i - 1);
48 //递归右边子数组
49 quickSort(a, i + 1, max);
50 }
51 }
【例4】棋盘覆盖,在一个2^k×2^k个方格组成的棋盘中,恰有一个方格与其他方格不同,称该方格为一特殊方格,且称该棋盘为一特殊棋盘。要用图示的4种不同形态的 L 型骨牌覆盖给定的特殊棋盘上除特殊方格以外的所有方格,且任意 2 个 L 型骨牌不得重叠覆盖。求如何覆盖。
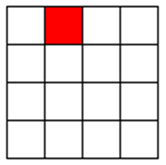
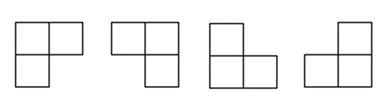
这是一个二维的位置问题,要在符合题目要求的情况下确定每个L型骨牌在棋盘中的位置,棋盘可以看成一个表格,用一个二维数组表示。举个例子,k取3吧,棋盘尺寸int size = 2^3;棋盘数组int[][] chessBoard = new int[size][ size];
设置一个特殊方格:chessBoard[0][1] = -1; 如图1,蓝色数字是数组下标表示的行列号,-1表示特殊方格,0表示空方格,每一个方格都有两个数组下标表示其位置,比如特殊方格表示为chessBoard[0][1] ;要放入L型骨牌就是在3个L型连着的空格填入同一个骨牌编号。骨牌编号:int l = 1; 放入1号骨牌:chessBoard[0][0] = l; chessBoard[1][0] = l;chessBoard[1][1] = l;
对于棋盘来说,L型骨牌是不规则的,要填满必须符合一定的规律,大棋盘不好找规律,就把棋盘分成小棋盘。如图2,一次分成四个小棋盘后,只有一个小棋盘有特殊方格,就把第一个L型骨牌放在另外三个小棋盘分界处,每个小棋盘分别占一个小棋盘的一个格,对这三个小棋盘来说,有一个空格被占了,就相当于有一个特殊方格,因为L型骨牌占3个方格,而棋盘格数是2的倍数,无论在什么位置只要棋盘中有一个被占方格,剩余的方格就能放满L型骨牌。所以此时四个小棋盘都是和原问题同样的问题,可以分别调用本方法,如图3,4,每次调用都把当前棋盘一分四同时确定一个骨牌的位置,直到小棋盘小到只有一个方格时,最后一个骨牌也能直接确定了。
因为最终的目的是把棋盘数组填满骨牌编号,没必要真的拆分棋盘数组,可以用棋盘的左上角格子的两个下标和棋盘尺寸确定一个子棋盘,每次分解棋盘只要修改三个整数变量就可以了。因为每次递归骨牌号要+1,在外部声明静态的骨牌号,方便累加,不会出现重复号码。

1 /*伪代码:
2 声明静态变量骨牌号
3 覆盖棋盘{
4 输入棋盘数组,数组的左上角方格行列下标,特殊方格行列下标,棋盘尺寸
5 棋盘尺寸=1时结束递归
6 棋盘尺寸/2,获得4个子棋盘
7 骨牌号++
8 if(特殊方格在左上角子棋盘) {
9 递归左上角子棋盘
10 }else {
11 把骨牌号填入右下角方格
12 递归左上角子棋盘
13 }
14 if(特殊方格在右上角子棋盘) {
15 递归右上角子棋盘
16 }else {
17 把骨牌号填入左下角方格
18 递归右上角子棋盘
19 }
20 if(特殊方格在左下角子棋盘) {
21 递归左下角子棋盘
22 }else {
23 把骨牌号填入右上角方格
24 递归左下角子棋盘
25 }
26 if(特殊方格在右下角子棋盘) {
27 递归右下角子棋盘
28 }else {
29 把骨牌号填入左上角方格
30 递归右下角子棋盘
31 }
32 }
33 */
34
35 //L型骨牌号,从1号开始
36 private static int brand = 1;
37 public static void main(String[] args) {
38 int k = 3;
39 //棋盘尺寸
40 int size = (int) Math.pow(2,k);
41 //棋盘数组,第一个下标表示行,第二个下标表示列
42 int[][] chessBoard = new int[size][size];
43 //确定特殊方格
44 chessBoard[0][1] = -1;
45 //调用覆盖棋盘的方法
46 overlayChessBoard(chessBoard,0,0,0,1,size);
47 //双层循环遍历二维数组
48 for (int i = 0; i <size ; i++) {
49 for (int j = 0; j <size ; j++) {
50 //每行的最后一个元素使用println打印,使下一个元素换行
51 if (j==size-1){
52 //打印小于10且不为-1的数时前面多加一个空格使整体对齐
53 if (chessBoard[i][j]<10 && chessBoard[i][j]!=-1){
54 System.out.println(" "+chessBoard[i][j]+" ");
55 }else {
56 System.out.println(chessBoard[i][j]+" ");
57 }
58 } else {
59 if (chessBoard[i][j]<10 && chessBoard[i][j]!=-1){
60 System.out.print(" "+chessBoard[i][j]+" ");
61 }else {
62 System.out.print(chessBoard[i][j]+" ");
63 }
64 }
65 }
66 }
67 }
68 /**用L型骨牌覆盖棋盘
69 * @param tr 当前(子)棋盘的左上角格子的行下标
70 * @param tc 当前(子)棋盘的左上角格子的列下标
71 * @param dr 当前(子)棋盘的特殊格子的行下标
72 * @param dc 当前(子)棋盘的特殊格子的列下标
73 * @param size 当前(子)棋盘的尺寸(边长)
74 * T(k)=O(4^k),S(k)=O(k)
75 */
76 private static void overlayChessBoard(int[][]chessBoard,int tr, int tc, int dr, int dc, int size){
77 //子棋盘尺寸为1时结束递归
78 if (size == 1) {
79 return;
80 }
81 //记录当前L型骨牌号并自增为下一次递归做准备
82 int l = brand++;
83 //分割当前棋盘并记录子棋盘尺寸(边长除以二,棋盘一分四),
84 int s = size/2;
85 //左上角子棋盘
86 if (dr <= tr+s-1 && dc <= tc+s-1) {
87 /*tr+s-1和tc+s-1是左上角子棋盘的右下角方格的行列下标,如果特殊方格的行列
88 下标小于或等于右下角方格的行列下标,则在此子棋盘中,递归左上角子棋盘。*/
89 overlayChessBoard(chessBoard,tr, tc, dr, dc, s);
90 } else { // 此棋盘中无特殊方格
91 // 用当前L型骨牌的编号l填充右下角方格。
92 chessBoard[tr+s-1][tc+s-1] = l;
93 //具有特殊方格就可以递归了,参数要更新特殊方格的行列下标
94 overlayChessBoard(chessBoard,tr, tc, tr+s-1, tc+s-1, s);}
95 // 右上角子棋盘
96 if (dr <= tr+s-1 && dc >= tc+s) {
97 /*tr+s-1和tc+s是右上角子棋盘的左下角方格行和列下标,如果特殊方格的行下标小于或等于左下
98 角方格的行下标,列下标大于或等于左下角方格的列下标,则在此子棋盘中,递归右上角子棋盘*/
99 overlayChessBoard(chessBoard,tr, tc+s, dr, dc, s);
100 } else {
101 //用当前L型骨牌的编号l填充左下角方格。
102 chessBoard[tr+s-1][tc+s] = l;
103 //递归右上角子棋盘
104 overlayChessBoard(chessBoard,tr, tc+s, tr+s-1, tc+s, s);}
105 // 左下角子棋盘
106 if (dr >= tr+s && dc <=tc+s-1) {
107 /*tr+s和tc+s-1是左下角子棋盘的右上角方格的行列下标,如果特殊方格的行下标大于或等于右上
108 角方格的行下标,列下标小于或等于右上角方格的列下标,则在此子棋盘中,直接递归左下角子棋盘。
109 否则用当前L型骨牌的编号l填充右上角方格再递归左下角子棋盘。*/
110 overlayChessBoard(chessBoard,tr+s, tc, dr, dc, s);
111 } else {
112 chessBoard[tr + s][tc + s - 1] = l;
113 overlayChessBoard(chessBoard,tr+s, tc, tr+s, tc+s-1, s);}
114 // 右下角子棋盘
115 if (dr >= tr+s && dc >= tc+s) {
116 /*tr+s和tc+s是此子棋盘的左上角方格的行和列下标,特殊方格的行列下标大于左上角方格的行列下标
117 就在此子棋盘中,直接递归右下角子棋盘。否则用当前L型骨牌的编号l填充左上角方格再递归右下角子棋盘。*/
118 overlayChessBoard(chessBoard,tr+s, tc+s, dr, dc, s);
119 } else {
120 chessBoard[tr + s][tc + s] = l;
121 overlayChessBoard(chessBoard,tr+s, tc+s, tr+s, tc+s,s);}
122 }
打印结果:

【例5】一维最接近点对问题:给一个点集s,s里的点分布在同一直线上,求相距最近的一个点对。
s中的 n 个点可化为直线坐标系上的 n 个有序实数 x1, x2,…, xn。最接近点对即为这 n 个实数中相差最小的 2 个实数。把每个点的对应的实数放入数组中,显然可以先给数组排序,然后用循环遍历数组对比相邻两个点的差就可以找出最接近点对。但是这种方法无法直接推广到二维和三维的情形。因此,对这种一维的简单情形,我们还是尝试用分治策略来求解,并希望能推广到二维和三维的情形。
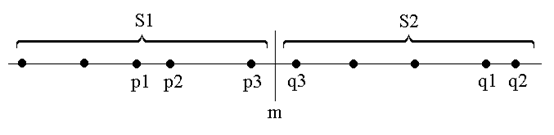
同样还是先把数组生序排列,模仿直线坐标系上的情况。然后把原问题分解成两个子问题。基于平衡子问题的思想,选取S中各点坐标的中位数m作为分割点将S划分为2个子集S1和S2。先在S1和S2上找出其最接近点对{p1,p2}和{q1,q2},然后再找出横跨S1和S2的最近点对{p3,q3},对比选出三者最小的就是S的最近点对。
首先考虑怎么求S1和S2中的最近点对,这是和原问题一样的子问题。对S1和S2递归,用同样的方法求S1和S2内的最近点对,一直递归到孙子数组只有一个点对时就可以直接相减求出点对距离了,如果孙子数组只有一个点,就设其距离为无限大,暂时忽略这个孙子数组,等到求跨两子数组的点对时再用到它。
然后考虑怎么求横跨两个子数组的最近点对,假如S1和S2的最近点对{p1,p2}和{q1,q2}都求出来了,对比得到当前S的最近点对的距离d=min{|p1-p2|,|q1-q2|},如果存在更近的点对{p3,q3},即|p3-q3|<d,则p3和q3两者与m的距离不超过d,即p3∈(m-d,m],q3∈[m,m+d),并且这两个区间都最多可能有一个点对(否则必有两点距离小于 d)。那我们就遍历S找到(m-d, m+d)内的所有点,即p3,q3,再判断是否存在|p3-q3|<d即可得到S的最近点对。在递归时这步操作也能帮子数组找到横跨两个孙子数组的最近点对。 因为一个点对有3个值,总是一起的,所以设一个类方便记录返回值。

1 private static class PairOfPoints{//点对类
2 int point1;
3 int point2;
4 int closestDist;//最近点对的距离
5 PairOfPoints(int point1, int point2, int closestDist) {
6 this.point1 = point1;
7 this.point2 = point2;
8 this.closestDist = closestDist;
9 }
10 }
11 public static void main(String[] args) {
12 int[] s = new int[10];
13 Random r = new Random();
14 System.out.println("S集内所有的点为:");
15 for (int i = 0; i <10 ; i++) {
16 //随机生成1-100的整数放入数组。
17 s[i]=r.nextInt(100)+1;
18 }//数组排序
19 Arrays.sort(s);
20 //打印原数组
21 System.out.println(Arrays.toString(s));
22 PairOfPoints pp = closestPairOfPoints(s);
23 System.out.println("最近点对是:["+pp.point1+","+pp.point2+"] 最近距离是:"+pp.closestDist);
24 }
25 private static boolean isOdd(int a){//判断奇偶数
26 //是奇数返回true,偶数返回false
27 return (a % 2) == 1;
28 }
29 private static PairOfPoints closestPairOfPoints(int[] s ) {
30 //当前数组的长度
31 int n = s.length;
32 //当前子数组长度为1时,返回一个点对对象,只记录一个点值,点对距离设为无限大。我选择用0表示没有点,点集s中的点都用>0的整数表示。
33 if (n == 1) {
34 return new PairOfPoints(s[0],0,Integer.MAX_VALUE);
35 }
36 //当前子数组长度为2时,返回一个点对对象,记录两个点值,点对距离为两点差的绝对值
37 if (n == 2) {
38 return new PairOfPoints(s[0],s[1],Math.abs(s[0]-s[1]));
39 }
40
41 int m;//中位数
42 int len1;//s1的数组长度
43 //判断当前数组长度奇偶性
44 boolean odd = isOdd(n);
45 if (odd){
46 //奇数个元素时中间一个元素为数组中位数
47 m = s[n/2];
48 //分割时s1多一个分一个元素
49 len1 = n/2+1;
50 } else {
51 //偶数个元素时中间两个元素平均数为数组中位数
52 m = (s[n/2-1]+s[n/2])/2;
53 len1 = n/2;
54 }
55 //根据长度复制数组
56 int[] s1 = Arrays.copyOf(s,len1);
57 //根据下标复制数组,s1的长度刚好是s2的开始下标
58 int[] s2 = Arrays.copyOfRange(s,len1,n);
59 //递归求解s1中最近点对
60 PairOfPoints pp1 = closestPairOfPoints(s1);
61 //递归求解s2中最近点对
62 PairOfPoints pp2 = closestPairOfPoints(s2);
63 //比较得出s1和s2内的最近点对
64 PairOfPoints pp0;
65 if (pp1.closestDist < pp2.closestDist) {
66 pp0 = pp1;
67 }else {
68 pp0 = pp2;
69 }//获得当前最近距离
70 int d = pp0.closestDist;
71 //跨s1和s2的点对。
72 PairOfPoints pp3 = new PairOfPoints(0,0,0);
73 //遍历S找到(m-d m+d)内的所有点
74 for (int i : s ) {
75 //因为数组s有奇数个元素时m在s1内,所以第一个点范围是(m-d,m]
76 if (i>(m-d)&&i<=m) {
77 pp3.point1 = i;
78 } //第二个点的范围是(m,m+d)
79 if (i>m && i<(m+d)) {
80 pp3.point2 = i;
81 }
82 }//如果(m-d m+d)内有两个点,相减得点对距离,否则距离为无限大
83 if (pp3.point1!=0 && pp3.point2!=0){
84 pp3.closestDist = Math.abs(pp3.point1-pp3.point2);
85 }else {
86 pp3.closestDist = Integer.MAX_VALUE;
87 }
88 //判断跨距离是否更小
89 if (pp3.closestDist<d) {
90 return pp3;
91 }
92 return pp0;
93 }
94 /*
95 打印结果:S集内所有的点为:
96 [27, 28, 32, 44, 57, 63, 90, 93, 94, 100]
97 最近点对是:[93,94] 最近距离是:1*/
【例6】二维最接近点对问题:给一个点集s,s里的点分布在同一平面上,求相距最近的一个点对。
s中的n个点可化为平面直角坐标系上的n个有序数对 (x1,y1),( x2,y2)…, (xn,yn),可以新设一个点类,每个点用一个点类对象存储,点集S用一个点类数组存储。两点的距离用勾股定理计算√((x1-x2)²+(y1-y2)²)。
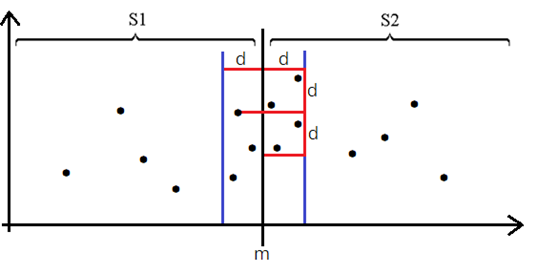
先把所有的点按x轴坐标值升序排列,模仿平面直角坐标系上的分布情况。然后把原问题分解成两个子问题。基于平衡子问题的思想,选取S中各点坐标的x值的中位数m,用直线x=m作为分割线将S划分为2个子集S1和S2。同样是递归地在S1和S2内找出其最接近点对{p1,p2}和{q1,q2},求出其距离d1和d2,设d=min{d1,d2},然后在x∈(m-d,m+d)内找跨两子集的最近点对。平面的情况这范围内可能有多个点。我们可以把在(m-d,m]和[m,m+d)内的点分别放入两个点集P1和P2,对于P1的每个点都在P2内找到一个y轴距离不大于d 的点组成点对,最后对比得出最近点对{p3,q3}和d3。再和d对比得出最终结果。

1 private static class Point implements Comparable<Point>{
2 /*二维点类,实现Comparable接口,该接口对实现它的每个类的对象强加一个整体排序。
3 这个排序被称为类的自然排序 ,类的compareTo方法被称为其自然比较方法 。*/
4 int x;
5 int y;
6 Point(int x, int y) {
7 this.x = x;
8 this.y = y;
9 }
10 @Override
11 public int compareTo(Point p) {
12 return this.x-p.x;/*将此对象与指定的对象进行比较以进行排序。
13 返回一个负整数,零或正整数,对应此对象小于,等于或大于指定对象。*/
14 }
15
16 Point() {
17 }
18 }
19 //点对类
20 private static class PairOfPoints{
21 Point point1;
22 Point point2;
23 //最近点对的距离
24 double closestDist;
25 PairOfPoints(Point point1, Point point2, double closestDist) {
26 this.point1 = point1;
27 this.point2 = point2;
28 this.closestDist = closestDist;
29 }
30 }
31 public static void main(String[] args){
32 //点类数组
33 Point[] s = new Point[10];
34 Random r = new Random();
35 for (int i = 0; i <10 ; i++) {
36 //用随机数创建一个点对象放入数组。
37 s[i] = new Point(r.nextInt(100)+1,r.nextInt(100)+1);
38 }//按x的升序排列
39 Arrays.sort(s);
40 System.out.println("S集内所有的点为:");
41 //打印原数组
42 for (Point p : s ) {
43 if (p == s[0]){
44 System.out.print("["+"("+p.x+","+p.y+")"+",");
45 } else if (p == s[s.length-1]){
46 System.out.println("("+p.x+","+p.y+")"+"]");
47 }else {
48 System.out.print("("+p.x+","+p.y+")"+",");
49 }
50 }
51 PairOfPoints pp = closestPairOfPoints(s);
52 System.out.println("最近点对是:[("+pp.point1.x+","+pp.point1.y+"),("
53 +pp.point2.x+","+pp.point2.y+")],最近距离是:"+pp.closestDist+"。");
54 }//勾股定理求距离
55 private static double distance(Point p1,Point p2){
56
57 return Math.sqrt(Math.pow((p2.x - p1.x),2)+Math.pow((p2.y - p1.y),2));
58 }
59 //判断奇偶数
60 private static boolean isOdd(int a){
61 //是奇数返回true
62 return (a % 2) == 1;
63 }
64 private static PairOfPoints closestPairOfPoints(Point[] s ) {
65 //当前数组的长度
66 int n = s.length;
67 //当前子数组长度为1时,返回一个点对对象,只记录一个点对象,点对距离设为无限大
68 if (n == 1) {
69 return new PairOfPoints(s[0],new Point(),Double.MAX_VALUE);
70 }
71 //当前子数组长度为2时,返回一个点对对象,记录两个点对象,点对距离用勾股定理计算
72 if (n == 2) {
73 return new PairOfPoints(s[0],s[1],distance(s[0],s[1]));
74 }
75 //中位数,分割线为x=m。
76 double m;
77 //s1的数组长度
78 int len1;
79 //判断当前数组长度奇偶性
80 boolean odd = isOdd(n);
81 if (odd){
82 //奇数个元素时中间一个元素的x值为数组中位数
83 m = s[n/2].x;
84 //分割时s1多一个分一个元素
85 len1 = n/2+1;
86 } else {//偶数个元素时中间两个元素平均数为数组中位数
87 m = (double) (s[n/2-1].x+s[n/2].x)/2;
88 len1 = n/2;
89 }//根据长度复制数组
90 Point[] s1 = Arrays.copyOf(s,len1);
91 //根据下标复制数组,s1的长度刚好是s2的开始下标
92 Point[] s2 = Arrays.copyOfRange(s,len1,n);
93 //递归求解s1中最近点对
94 PairOfPoints pp1 = closestPairOfPoints(s1);
95 //递归求解s2中最近点对
96 PairOfPoints pp2 = closestPairOfPoints(s2);
97 //比较得出s1和s2内的最近点对
98 PairOfPoints pp0;
99 if (pp1.closestDist < pp2.closestDist) {
100 pp0 = pp1;
101 }else {
102 pp0 = pp2;
103 }//获得当前最近距离
104 double d = pp0.closestDist;
105 //临时记录x∈(m-d,m]内的点对象,因为不知数量所以用ArrayList
106 ArrayList<Point> p1 = new ArrayList<>();
107 //临时记录x∈(m,m+d)内的点对象,(数组s有奇数个元素时x=m的点对象在s1内)
108 ArrayList<Point> p2 = new ArrayList<>();
109 //遍历S集
110 for (Point i : s ) {
111 //把x∈(m-d,m]的点放入p1
112 if (i.x>(m-d)&&i.x<=m) {
113 p1.add(i);
114 }
115 //把x∈(m,m+d)的点放入p2
116 if (i.x<(m+d)&&i.x>m) {
117 p2.add(i);
118 }
119 }
120 PairOfPoints pp3 = new PairOfPoints(new Point(),new Point(),Double.MAX_VALUE);
121 //先遍历p1,
122 for ( Point i : p1 ) {
123 //再遍历p2,
124 for (Point j: p2 ) {
125 //p1每个点都和p2内y轴距离不大于d的点组成一个点对
126 if (j.y<=i.y+d && j.y>=i.y-d){
127 //如果当前点对距离小于之前记录的点对就更新数据
128 if (distance(i,j)<pp3.closestDist){
129 //最终获得一个跨子数组的点对
130 pp3 = new PairOfPoints(i,j,distance(i,j));
131 }
132 }
133 }
134 }//判断跨距离是否更小
135 if (pp3.closestDist<d) {
136 return pp3;
137 }
138 return pp0;
139 }
140 /*打印结果:S集内所有的点为:
141 [(2,43),(16,95),(65,49),(73,100),(79,93),(80,52),(83,85),(87,93),(93,71),(96,80)]
142 最近点对是:[(79,93),(87,93)],最近距离是:8.0。*/
【例7】三维最接近点对问题:给一个点集s,s里的点分布在同一平面上,求相距最近的一个点对。
三维的情况和二维情况的操作一样,只是在对比p1和p2内的点时多加一个限制,对于P1的每个点都在P2内找到一个y轴和z轴距离都不大于d 的点组成点对,最后对比得出最近点对{p3,q3}和d3。再和d对比得出最终结果。

1 private static class Point implements Comparable<Point>{
2 /*二维点类,实现Comparable接口,该接口对实现它的每个类的对象强加一个整体排序。 这个排序被称为类的自然排序 ,类的compareTo方法被称为其自然比较方法 。*/
3 int x;
4 int y;
5 int z;
6
7 Point(int x, int y, int z) {
8 this.x = x;
9 this.y = y;
10 this.z = z;
11 }
12 Point() {//空点
13 }
14 @Override
15 public int compareTo(Point p) {
16 return this.x-p.x;/*将此对象与指定的对象进行比较以进行排序。
17 返回一个负整数,零或正整数,对应此对象小于,等于或大于指定对象。*/
18 }
19 }
20 private static class PairOfPoints{//点对类
21 Point point1;
22 Point point2;
23 double closestDist;//最近点对的距离
24 PairOfPoints(Point point1, Point point2, double closestDist) {
25 this.point1 = point1;
26 this.point2 = point2;
27 this.closestDist = closestDist;
28 }
29 }
30 public static void main(String[] args){
31 //点类数组
32 Point[] s = new Point[10];
33 Random r = new Random();
34 for (int i = 0; i <10 ; i++) {
35 //用随机数创建一个点对象放入数组。
36 s[i] = new Point(r.nextInt(100)+1,r.nextInt(100)+1,r.nextInt(100)+1);
37 }//按x的升序排列
38 Arrays.sort(s);
39 System.out.println("S集内所有的点为:");
40 //打印原数组
41 for (Point p : s ) {
42 if (p == s[0]){
43 System.out.print("["+"("+p.x+","+p.y+","+p.z+")"+",");
44 } else if (p == s[s.length-1]){
45 System.out.println("("+p.x+","+p.y+","+p.z+")"+"]");
46 }else {
47 System.out.print("("+p.x+","+p.y+","+p.z+")"+",");
48 }
49 }
50 PairOfPoints pp = closestPairOfPoints(s);
51 System.out.println("最近点对是:[("+pp.point1.x+","+pp.point1.y+","+pp.point1.z+"),("
52 +pp.point2.x+","+pp.point2.y+","+pp.point2.z+")],最近距离是:"+pp.closestDist+"。");
53 }
54
55 private static double distance(Point p1,Point p2){//勾股定理求距离
56 return Math.sqrt(Math.pow((p2.x - p1.x),2)+Math.pow((p2.y - p1.y),2)+Math.pow((p2.z - p1.z),2));
57 }//判断奇偶数
58 private static boolean isOdd(int a){
59 //是奇数返回true
60 return (a % 2) == 1;
61 }
62 private static PairOfPoints closestPairOfPoints(Point[] s ) {
63 int n = s.length;//当前数组的长度
64 //当前子数组长度为1时,返回一个点对对象,只记录一个点对象,点对距离设为无限大
65 if (n == 1) {
66 return new PairOfPoints(s[0],new Point(),Double.MAX_VALUE);
67 }
68 //当前子数组长度为2时,返回一个点对对象,记录两个点对象,点对距离用勾股定理计算
69 if (n == 2) {
70 return new PairOfPoints(s[0],s[1],distance(s[0],s[1]));
71 }//中位数,分割面为x=m。
72 double m;
73 //s1的数组长度
74 int len1;
75 //判断当前数组长度奇偶性
76 boolean odd = isOdd(n);
77 if (odd){
78 //奇数个元素时中间一个元素的x值为数组中位数
79 m = s[n/2].x;
80 //分割时s1多一个分一个元素
81 len1 = n/2+1;
82 } else {
83 //偶数个元素时中间两个元素平均数为数组中位数
84 m = (double) (s[n/2-1].x+s[n/2].x)/2;
85 len1 = n/2;
86 }//根据长度复制数组
87 Point[] s1 = Arrays.copyOf(s,len1);
88 //根据下标复制数组,s1的长度刚好是s2的开始下标
89 Point[] s2 = Arrays.copyOfRange(s,len1,n);
90 //递归求解s1中最近点对
91 PairOfPoints pp1 = closestPairOfPoints(s1);
92 //递归求解s2中最近点对
93 PairOfPoints pp2 = closestPairOfPoints(s2);
94 //比较得出s1和s2内的最近点对
95 PairOfPoints pp0;
96 if (pp1.closestDist < pp2.closestDist) {
97 pp0 = pp1;
98 }else {
99 pp0 = pp2;
100 }//获得当前最近距离
101 double d = pp0.closestDist;
102 //临时记录x∈(m-d,m]内的点对象,因为不知数量所以用ArrayList
103 ArrayList<Point> p1 = new ArrayList<>();
104 //临时记录x∈(m,m+d)内的点对象,(数组s有奇数个元素时x=m的点对象在s1内)
105 ArrayList<Point> p2 = new ArrayList<>();
106 //遍历S集
107 for (Point i : s ) {
108 //把x∈(m-d,m]的点放入p1
109 if (i.x>(m-d)&&i.x<=m) {
110 p1.add(i);
111 }
112 //把x∈(m,m+d)的点放入p2
113 if (i.x<(m+d)&&i.x>m) {
114 p2.add(i);
115 }
116 }
117 PairOfPoints pp3 = new PairOfPoints(new Point(),new Point(),Double.MAX_VALUE);
118 //先遍历p1,再遍历p2,
119 for ( Point i : p1 ) {
120 for (Point j: p2 ) {
121 //p1每个点都和p2内y轴距离不大于d的点组成一个点对
122 if (j.y<=i.y+d && j.y>=i.y-d && j.z<=i.z+d && j.z>=i.z-d){
123 //如果当前点对距离小于之前记录的点对就更新数据
124 if (distance(i,j)<pp3.closestDist){
125 //最终获得一个跨子数组的点对
126 pp3 = new PairOfPoints(i,j,distance(i,j));
127 }
128 }
129 }
130 }
131 if (pp3.closestDist<d)
132 //判断跨距离是否更小
133 {
134 return pp3;
135 }
136 return pp0;
137 }
138 /*打印结果:S集内所有的点为:
139 [(3,3,1),(10,9,55),(27,71,15),(29,96,99),(29,15,20),(42,61,9),(47,24,63),(73,39,95),(76,20,30),(91,79,50)]
140 最近点对是:[(27,71,15),(42,61,9)],最近距离是:19.0。*/
【例8】循环赛日程表问题设计 n = 2k选手满足以下要求的比赛日程表:
(1) 每个选手必须与其他 n - 1 个选手各赛一次;
(2) 每个选手一天只能赛一次;
(3) 循环赛一共进行 n - 1 天。
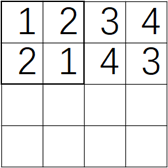
比赛日程表是二维表,要分治最好一分四,那么行数和列数必须相等且是2的倍数。选手数是n,比赛天数是n-1,因此设计日程表的格式时可以把每个选手的日程用一行表示,每一行的第1格是选手号,第2—n格是当前选手第1—n-1天的对手号。这样比赛日程表的行数和列数都是n。这样就有了分治的前提条件。
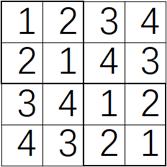
确定了日程表格式就要找规律。假设有4个选手,先确定第一个选手的比赛日程,直接把4个选手号顺序填入表格。然后确定第二个选手日程时要考虑与第一行错开,第一天上一行是2,这一行就是1,上面3下面4,上面4下面3。最终确定第二行时发现只要每个四方格的对角数字相等就能保证两个选手的日程不冲突。试着把四格当一格,根据对角数字相等的规律,由一二行推导出三四行的数字,发现依然不冲突,由此可知此规律可用。那么无论表多大,第一列和第一行的数字都是确定的,然后用分治策略分成最小的四方格就可以确定其中的数字从而确定整张表的数字。
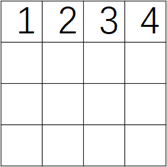

1 private static int k = 3;
2 private static int n = (int) Math.pow(2,k);
3 private static int[][] calendar = new int[n][n];
4 public static void main(String[] args) {
5 for (int i = 0; i < n; i++) {
6 //输入第一行的数据
7 calendar[0][i] = i + 1;
8 }
9 generateCalendar(2);
10 //双层循环遍历二维数组
11 for (int i = 0; i < n; i++) {
12 for (int j = 0; j < n; j++) {
13 if (j == n - 1) {
14 //每行的最后一个元素使用println打印,使下一个元素换行
15 if (calendar[i][j] < 10) {
16 /*打印小于10的数时前面多加一个空格使整体对齐*/
17 System.out.println(" " + calendar[i][j] + " ");
18 } else {
19 System.out.println(calendar[i][j] + " ");
20 }
21 } else {
22 if (calendar[i][j] < 10) {
23 System.out.print(" " + calendar[i][j] + " ");
24 } else {
25 System.out.print(calendar[i][j] + " ");
26 }
27 }
28 }
29 }
30 }
31 private static void generateCalendar( int currRow){//当前行数
32 if (currRow > n) {
33 return;
34 }//当前四方格的尺寸
35 int s4 = currRow;
36 //循环次数=方格数
37 for (int i = 0; i <n/s4 ; i++) {
38 //四方格的每个方格尺寸
39 int s1 = s4/2;
40 //第几个方格
41 int s2 = s4*i;
42 for (int j = 0; j < s1; j++) {
43 for (int l = 0; l < s1; l++) {
44 //对角复制
45 calendar[s1+j][s1+s2+l] = calendar[j][s2+l];
46 calendar[s1+j][s2+l] = calendar[j][s1+s2+l];
47 }
48 }
49 }
50 currRow *= 2;
51 generateCalendar(currRow);
52 }
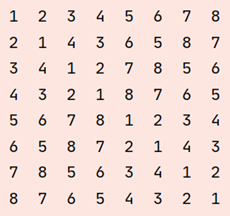
打印结果:
![]()
![]()




 浙公网安备 33010602011771号
浙公网安备 33010602011771号