java算法篇之二：栈和队列

本文实现基于上一章实现的自定义数组：https://blog.csdn.net/u012575432/article/details/106240615

1. 自定义栈

栈是一种先进后出的线性结构。栈可以用于记录递归方法调用的中断点、撤销操作等。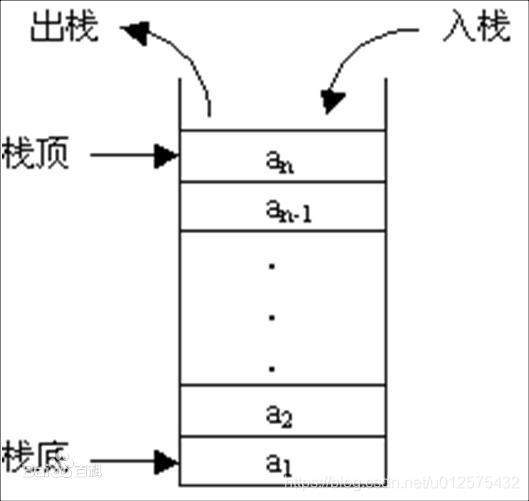

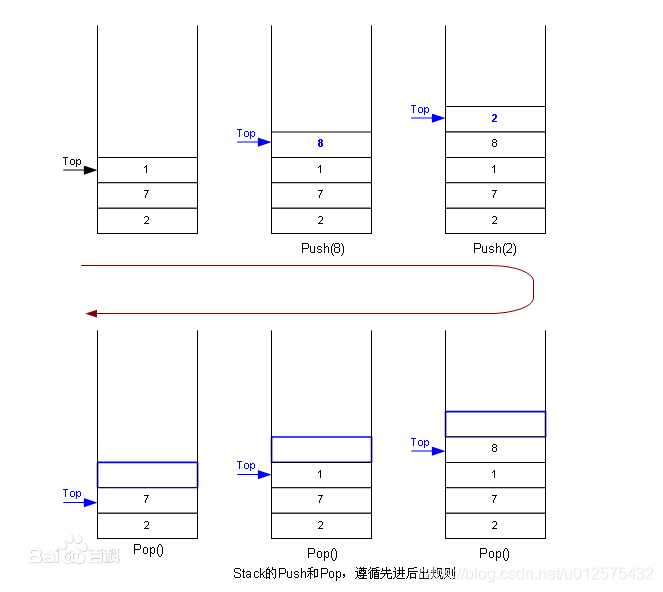
• 在Array.java中新增如下方法

  // 获取最后一个位置的元素
  public E getLast() {
      return get(size - 1);
  }
  
  // 获取第一个位置的元素
  public E getFirst() {
      return get(0);
  }
  

• 新增Stack接口，内容如下

  public interface Stack<E> {
  
      // 获取栈大小
      int getSize();
  
      // 栈是否为空
      boolean isEmpty();
  
      // 向栈中添加元素
      void push(E e);
  
      // 取出栈顶元素
      E pop();
  
      // 查看栈顶元素，但是元素不需要进行出栈操作
      E peek();
  
  }
  

• 新增ArrayStack实现类，内容如下

  public class ArrayStack<E> implements Stack<E> {
  
      Array<E> array;
  
      public ArrayStack(int capacity) {
          array = new Array<>(capacity);
      }
  
      public ArrayStack() {
          array = new Array<>();
      }
  
      @Override
      public int getSize() {
          return array.getSize();
      }
  
      @Override
      public boolean isEmpty() {
          return array.isEmpty();
      }
  
      @Override
      public void push(E e) {
          array.addLast(e);
      }
  
      @Override
      public E pop() {
          return array.removeLast();
      }
  
      @Override
      public E peek() {
          return array.getLast();
      }
  
      private int getCapacity() {
          return array.getCapacity();
      }
  
      @Override
      public String toString() {
          StringBuilder res = new StringBuilder();
          res.append("Stack: ");
          res.append("[");
          for (int i = 0; i < array.getSize(); i++) {
              res.append(array.get(i));
              if (i != array.getSize() - 1) {
                  res.append(", ");
              }
          }
          res.append("] top");
          return res.toString();
      }
  }
  

2. 自定义队列

• 队列也是一种先进先出的线性结构
• 相比数组，队列对应的操作时数组的子集
• 只能从一端（队尾）添加元素，只能从另一端（队首）取出元素

2.1 数组队列

• 新增Queue接口，内容如下

  public interface Queue<E> {
  
      // 获取队列大小
      int getSize();
  
      // 队列是否为空
      boolean isEmpty();
  
      // 入队
      void enqueue(E e);
  
      // 出队
      E dequeue();
  
      // 获取队首元素，但不进行出队操作
      E getFront();
  
  }
  

• 新增ArrayQueue实现类，内容如下

  public class ArrayQueue<E> implements Queue<E> {
      private Array<E> array;
  
      public ArrayQueue(int capacity) {
          this.array = new Array<>(capacity);
      }
  
      public ArrayQueue() {
          this.array = new Array<>();
      }
  
      @Override
      public int getSize() {
          return this.array.getSize();
      }
  
      @Override
      public boolean isEmpty() {
          return this.array.isEmpty();
      }
  
      @Override
      public void enqueue(E e) {
          array.addLast(e);
      }
  
      @Override
      public E dequeue() {
          return array.removeFirst();
      }
  
      @Override
      public E getFront() {
          return array.getFirst();
      }
  
      @Override
      public String toString() {
          StringBuilder res = new StringBuilder();
          res.append("Queue: ");
          res.append("front [");
          for (int i = 0; i < array.getSize(); i++) {
              res.append(array.get(i));
              if (i != array.getSize() - 1) {
                  res.append(", ");
              }
          }
          res.append("] tail");
          return res.toString();
      }
  }
  

2.2 循环队列

• 新增LoopQueue实现类

  public class LoopQueue<E> implements Queue<E> {
  
      private E[] data;
      private int front, tail, size;
  
      public LoopQueue(int capacity) {
          this.data = (E[]) new Object[capacity + 1];
          this.front = 0;
          this.tail = 0;
          this.size = 0;
      }
  
      public LoopQueue() {
          this(10);
      }
  
      @Override
      public int getSize() {
          return this.size;
      }
  
      @Override
      public boolean isEmpty() {
          return this.front == this.tail;
      }
  
      @Override
      public void enqueue(E e) {
          if ((this.tail + 1) % this.data.length == this.front)
              this.resize(this.getCapaticy() * 2);
  
          this.data[this.tail] = e;
          this.tail = (this.tail + 1) % this.data.length;
          this.size++;
      }
  
      @Override
      public E dequeue() {
          if (this.isEmpty())
              throw new IllegalArgumentException("Cannot dequeue from an empty queue.");
  
          E ret = this.data[this.front];
          this.data[this.front] = null;
          this.front = (this.front + 1) % this.data.length;
          this.size--;
  
          if (this.size == this.getCapaticy() / 4 && this.getCapaticy() / 2 != 0)
              this.resize(this.getCapaticy() / 2);
          return ret;
      }
  
      @Override
      public E getFront() {
          if (this.isEmpty())
              throw new IllegalArgumentException("Queue is empty.");
  
          return this.data[this.front];
      }
  
      private int getCapaticy() {
          return this.data.length - 1;
      }
  
      private void resize(int newCapacity) {
          E[] newData = (E[]) new Object[newCapacity + 1];
          for (int i = 0; i < this.size; i++) {
              newData[i] = this.data[(front + i) % this.data.length];
          }
          data = newData;
          front = 0;
          tail = size;
      }
  
      @Override
      public String toString() {
          StringBuilder res = new StringBuilder();
          res.append(String.format("Queue: size = %d, capacity = %d\n", this.size, this.getCapaticy()));
          res.append("front [");
          for (int i = this.front; i != this.tail; i = (i + 1) % this.data.length) {
              res.append(this.data[i]);
              if ((i + 1) % this.data.length != this.tail) {
                  res.append(", ");
              }
          }
          res.append("] tail");
          return res.toString();
      }
  }
  

2.3 时间复杂度分析

均摊复杂度：大部分情况下时间复杂度很低，极个别情况下时间复杂度比较高，此时将较高的时间复杂度的操作耗时平均到时间复杂度较低的操作上。

eg：比如向数组中添加元素时，大部分情况下的时间复杂度为O(1)，但是当触发扩容的时候时间复杂度为O(n)。也就是当数组容量为n时，第n+1次操作会触发扩容，总共进行了2n+1次操作；也就是n+1次新增触发了2n+1次操作，平均每次新增操作进行2次基本操作。所以均摊时间复杂度也为O(1)

数组队列和循环队列的差别主要在dequeue操作上，由于数组队列每次dequeue都需要将全部数据往前移，所以时间复杂度为O(n)，而循环队列的dequeue的均摊复杂度仅为O(1)。因此在性能上循环队列更好。

个人测试，进行10W次enqueue操作，然后再进行10W次dequeue操作，数组队列和循环队列耗费时间如下