《A Survey on Transfer Learning》迁移学习研究综述 翻译

迁移学习研究综述

Sinno Jialin Pan and Qiang Yang,Fellow, IEEE
摘要：
  在许多机器学习和数据挖掘算法中，一个重要的假设就是目前的训练数据和将来的训练数据，一定要在相同的特征空间并且具有相同的分布。然而，在许多现实的应用案例中，这个假设可能不会成立。比如，我们有时候在某个感兴趣的领域有个分类任务，但是我们只有另一个感兴趣领域的足够训练数据，并且后者的数据可能处于与之前领域不同的特征空间或者遵循不同的数据分布。这类情况下，如果知识的迁移做的成功，我们将会通过避免花费大量昂贵的标记样本数据的代价，使得学习性能取得显著的提升。近年来，为了解决这类问题，迁移学习作为一个新的学习框架出现在人们面前。这篇综述主要聚焦于当前迁移学习对于分类、回归和聚类问题的梳理和回顾。在这篇综述中，我们主要讨论了其他的机器学习算法，比如领域适应、多任务学习、样本选择偏差以及协方差转变等和迁移学习之间的关系。我们也探索了一些迁移学习在未来的潜在方法的研究。

关键词： 迁移学习；综述；机器学习；数据挖掘

1 引言

  数据挖掘和机器学习已经在许多知识工程领域实现了巨大成功，比如分类、回归和聚类。然而，许多机器学习方法仅在一个共同的假设的前提下：训练数据和测试数据必须从同一特种空间中获得，并且需要具有相同的分布。当分布情况改变时，大多数的统计模型需要使用新收集的训练样本进行重建。在许多现实的应用中，重新收集所需要的训练数据来对模型进行重建，是需要花费很大代价或者是不可能的。如果降低重新收集训练数据的需求和代价，那将是非常不错的。在这些情况下，在任务领域之间进行知识的迁移或者迁移学习，将会变得十分有必要。

  许多知识工程领域的例子，都能够从迁移学习中真正获益。举一个网页文件分类的例子。我们的目的是把给定的网页文件分类到几个之前定义的目录里。作为一个例子，在网页文件分类中，可能是根据之前手工标注的样本，与之关联的分类信息，而进行分类的大学网页。对于一个新建网页的分类任务，其中，数据特征或数据分布可能不同，因此就出现了已标注训练样本的缺失问题。因此，我们将不能直接把之前在大学网页上的分类器用到新的网页中进行分类。在这类情况下，如果我们能够把分类知识迁移到新的领域中是非常有帮助的。

  当数据很容易就过时的时候，对于迁移学习的需求将会大大提高。在这种情况下，一个时期所获得的被标记的数据将不会服从另一个时期的分布。例如室内wifi定位问题，它旨在基于之前wifi用户的数据来查明用户当前的位置。在大规模的环境中，为了建立位置模型来校正wifi数据，代价是非常昂贵的。因为用户需要在每一个位置收集和标记大量的wifi信号数据。然而，wifi的信号强度可能是一个时间、设备或者其他类型的动态因素函数。在一个时间或一台设备上训练的模型可能导致另一个时间或设备上位置估计的性能降低。为了减少再校正的代价，我们可能会把在一个时间段（源域）内建立的位置模型适配到另一个时间段（目标域），或者把在一台设备(源域)上训练的位置模型适配到另一台设备（目标域）上。

  对于第三个例子，关于情感分类的问题。我们的任务是自动将产品（例如相机品牌）上的评论分类为正面和负面意见。对于这些分类任务，我们需要首先收集大量的关于本产品和相关产品的评论。然后我们需要在与它们相关标记的评论上，训练分类器。因此，关于不同产品牌的评论分布将会变得十分不一样。为了达到良好的分类效果，我们需要收集大量的带标记的数据来对某一产品进行情感分类。然而，标记数据的过程可能会付出昂贵的代价。为了降低对不同的产品进行情感标记的注释，我们将会训练在某一个产品上的情感分类模型，并把它适配到其它产品上去。在这种情况下，迁移学习将会节省大量的标记成本。

  在这篇文章中，我们给出了在机器学习和数据挖掘领域，迁移学习在分类、回归和聚类方面的发展。同时，也有在机器学习方面的文献中，大量的迁移学习对增强学习的工作。然而，在这篇文章中，我们更多的关注于在数据挖掘及其相近的领域，关于迁移学习对分类、回归和聚类方面的问题。通过这篇综述，我们希望对于数据挖掘和机器学习的团体能够提供一些有用的帮助。

  接下来本文的组织结构如下：在接下来的四个环节，我们先给出了一个总体的全览，并且定义了一些接下来用到的标记。然后，我们简短概括一下迁移学习的发展历程，同时给出迁移学习的统一定义，并将迁移学习分为三种不同的设置（在图2和表2中给出）。我们对于每一种设置回顾了不同的方法，在表3中给出。之后，在第6节，我们回顾了一些当前关于“负迁移”这一话题的研究，即那些发生在对知识迁移的过程中，产生负面影响的时候。在第7节，我们介绍了迁移学习的一些成功的应用，并且列举了一些已经发布的关于迁移学习数据集和工具包。最后在结论中，我们展望了迁移学习的发展前景。

2 概述

2.1 有关迁移学习的简短历史

  传统的数据挖掘和机器学习算法通过使用之前收集到的带标记的数据或者不带标记的数据进行训练，进而对将来的数据进行预测。在版监督分类中这样标注这类问题，即带标记的样本太少，以至于只使用大量未标记的样本数据和少量已标记的样本数据不能建立良好的分类器。监督学习和半监督学习分别对于缺失数据集的不同已经有人进行研究过。例如周和吴研究过如何处理噪音类标记的问题。杨认为当增加测试时，可以使得代价敏感的学习作为未来的样本。尽管如此，他们中的大多数假定的前提是带标记或者是未标记的样本都是服从相同分布的。相反，迁移学习允许训练和测试的域、任务以及分布是不同的。在现实中我们可以发现很多迁移学习的例子。例如我们可能发现，学习如何辨认苹果将会有助于辨认梨子。类似的，学会弹电子琴将会有助于学习钢琴。对于迁移学习研究的驱动，是基于事实上，人类可以智能地把先前学习到的知识应用到新的问题上进而快速或者更好的解决新问题。最初的关于迁移学习的研究是在NIPS-95研讨会上，机器学习领域的一个研讨话题“学会学习”，就是关注于保留和重用之前学到的知识这种永久的机器学习方法。

  自从1995年开始，迁移学习就以不同的名字受到了越来越多人的关注：学会学习、终生学习、知识迁移、感应迁移、多任务学习、知识整合、前后敏感学习、基于感应阈值的学习、元学习、增量或者累积学习。所有的这些，都十分接近让迁移学习成为一个多任务学习的一个框架这样的学习技术，即使他们是不同的，也要尽量学习多项任务。多任务学习的一个典型的方法是揭示是每个任务都受益的共同（潜在）特征。

  在2005年，美国国防部高级研究计划局的信息处理技术办公室发表的代理公告，给出了迁移学习的新任务：把之前任务中学习到的知识和技能应用到新的任务中的能力。在这个定义中，迁移学习旨在从一个或者多个源任务中提取信息，进而应用到目标任务上。与多任务学习相反，迁移学习不是同时学习源目标和任务目标的内容，而是更多的关注与任务目标。在迁移学习中，源任务和目标任务不再是对称的。

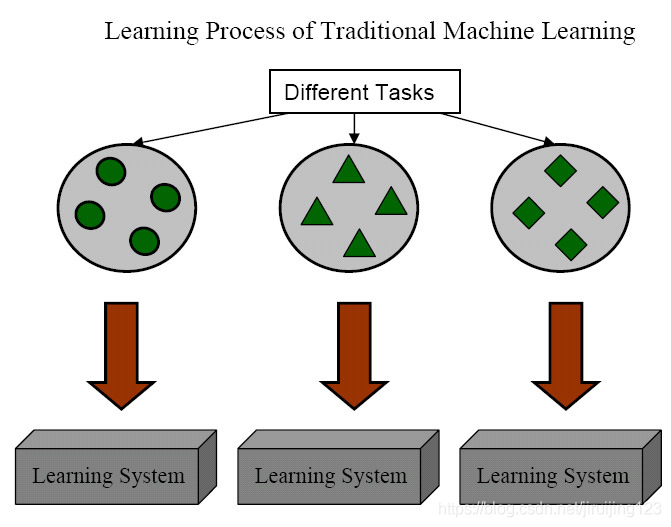
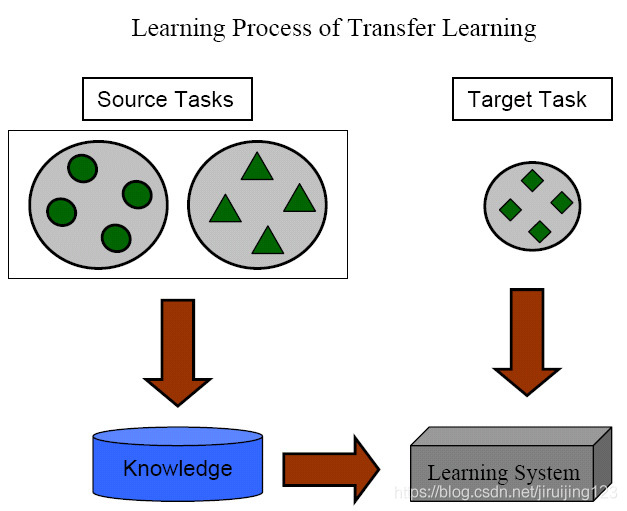
Fig. 1. Different Learning Processes between TraditionalMachine Learning and Transfer Learning
  图1展示了传统的学习和迁移学习的学习过程之间的不同。我们可以看到，传统的机器学习技术致力于从每个任务中抓取信息，而迁移学习致力于当目标任务缺少高质量的训练数据时，从之前任务向目标任务迁移知识。

  如今，迁移学习出现在许多顶级期刊上，令人注意的数据挖掘（比如ACM KDD,IEEE ICDM和PKDD），机器学习(比如ICML,ICDM和PKDD）和应用在数据挖掘和机器学习（比如ACM SIGIR,WWW和ACL）上。在我们给出迁移学习不同的类别的时候，我们首先描述一下本文中用到的符号。

2.2 符号和定义

  在本节中，我们介绍了本文中使用的一些符号和定义。首先，我们分别给出“域”和“任务"的定义。

  在本综述中，域 \(\mathcal{D}\) 包含两部分：一个特征空间 \(\mathcal{X}\)和一个边缘概率分布\(P(X)\)。其中 \(X=\{x_1, x_2, ..., x_n\} \in \mathcal{X}\)。比如我们的学习任务是文本分类，每一个术语被用作一个二进制特征，然后\(\mathcal{X}\)就是所有的术语向量的空间，\(x_i\)是第\(i\)个与一些文本相关的术语向量。X是一个特别的学习样本。总的来说，如果两个域不同，那么它们会有不同的特征空间或者服从不同的边缘概率分布。

  给定一个具体的域，\(\mathcal{D}=\{\mathcal{X}, P(X)\}\)，一个任务由两部分组成：一个标签空间 \(\mathcal{Y}\)和一个目标预测函数\(f(\cdot)\)（由\(\mathcal{T}=\{\mathcal{Y},f(\cdot)\}\)表示）。任务不可被直观观测，但是可以通过训练数据学习得来。任务由pair\(\{x_i, y_i\}\)组成，且\(x_i \in X, y_i \in \mathcal{Y}\)。函数\(f(\cdot)\)可用于预测新的例子\(x\)的标签\(f(x)\)。从概率学角度看，\(f(x)\)也可被写为\(P(y|x)\)。 在我们的文本分类例子里，\(\mathcal{Y}\)是所有标签的空间，对二元分类任务来说，就是“真”和“假”，\(y_i\)j就是“真”或“假”。
  简化起见，本文中我们只考虑一个源域\(\mathcal{D}_S\)和一个目标域\(\mathcal{D}_T\)。更准确点，用 \(\mathcal{D}_S=\{(x_{S_1}, y_{S_1})， ... , (x_{S_{n_S}}, y_{S_{n_S}})\}\), 其中\(x_{S_i} \in \mathcal{X}_S\)表示数据实例, \(y_{S_i} \in \mathcal{Y}_S\) 是对应的分类标签。在文档分类例子中，\(\mathcal{D}_S\)是文档对象向量及对应的真或假标签的集合。相似地，目标域记作： \(\mathcal{D}_T=\{(x_{T_1}, y_{T_1})， ... , (x_{T_{n_T}}, y_{T_{n_T}})\}\), 其中输入\(x_{T_i} \in \mathcal{X}_S\)， \(y_{T_i} \in \mathcal{Y}_T\)是对应的输出。多数情况下源域观测样本数目\(n_S\)与目标域观测样本数目\(n_T\)之间有如下关系：\(0≤n_T\ll n_S\)。
  现在我们给出迁移学习的统一定义：
Definition 1 (Transfer learning): 给定源域\(\mathcal{D}_S\)和学习任务\(\mathcal{T}_S\)，一个目标域\(\mathcal{D}_T\)和学习任务\(\mathcal{T}_T\)，迁移学习致力于用\(\mathcal{D}_S\)和\(\mathcal{T}_S\)中的知识，帮助提高\(\mathcal{D}_T\)中目标预测函数\(f_T(\cdot)\)的学习。并且有\(\mathcal{D}_S\)≠\(\mathcal{D}_T\)或\(\mathcal{T}_S\)≠\(\mathcal{T}_T\)。

在上面定义中，\(\mathcal{D}=\{\mathcal{X},P(X)\}\)，条件\(\mathcal{D}_S\)≠\(\mathcal{D}_T\)意味着源域和目标域实例不同\(\mathcal{X}_S\)≠\(\mathcal{X}_T\)或者源域和目标域边缘概率分布不同\(P_S(X)\)≠\(P_T(X)\)。同理\(\mathcal{T}=\{\mathcal{Y},P(Y|X)\}\)，\(\mathcal{T}_S\)≠\(\mathcal{T}_T\)意味着源域和目标域标签不同（\(\mathcal{Y}_S\)≠\(\mathcal{Y}_T\)）或者源域和目标域条件概率分布不同（\(P(Y_S|X_S)\)≠\(P(Y_T|X_T)\)）。当源域和目标域相同\(\mathcal{D}_S\)=\(\mathcal{D}_T\)且源任务和目标任务相同\(\mathcal{T}_S\)=\(\mathcal{T}_T\)，则学习问题变成一个传统机器学习问题。

以文档分类为例，域不同有以下两种情况：

1. 特征空间不同，即\(\mathcal{X}_S\)≠\(\mathcal{X}_T\)。可能是文档的语言不同。
2. 特征空间相同但边缘分布不同，即\(P(X_S)\)≠\(P(X_T)\),其中\(X_{S_i}\in\mathcal{X}_S\)，\(X_{T_i}\in\mathcal{X}_T\)。可能是文档主题不同。

给定域\(\mathcal{D}_S\)和\(\mathcal{D}_T\)，学习任务不同可能有以下两种情况：

1. 域间标签空间不同，即\(\mathcal{Y}_S\)≠\(\mathcal{Y}_T\)。可能是源域中文档需要分两类，目标域需要分十类。
2. 域间条件概率分布不同，即\(P(Y_S|X_S)\)≠\(P(Y_T|X_T)\)。
   除此之外，当两个域或者特征空间之间无论显式或隐式地存在某种关系时，我们说源域和目标域相关。

2.3迁移学习分类

迁移学习主要有以下三个研究问题：1）迁移什么，2）如何迁移，3）何时迁移。
“迁移什么”提出了迁移哪部分知识的问题。 一些知识对单独的域或任务有用，一些知识对不同的领域是通用的，可以用来提高目标域或目标任务的性能。
“何时迁移”提出了哪种情况下运用迁移学习。当源域和目标域无关时，强行迁移可能并不会提高目标域上算法的性能，甚至会损害性能。这种情况称为负迁移。当前大部分关于迁移学习的工作关注于“迁移什么”和“如何迁移”，隐含着一个假设：源域和目标域彼此相关。然而，如何避免负迁移是一个很重要的问题。
基于迁移学习的定义，我们归纳了传统机器学习方法和迁移学习的异同见下表。

1. 推导迁移学习（inductive transfer learning）（也叫归纳迁移学习¹）
   目标任务和源任务不同，无论目标域与源域是否相同。
   这种情况下，要用目标域中的一些已标注数据生成一个客观预测模型\(f(\cdot)\)以应用到目标域中。除此之外，根据源域中已标注和未标注数据的不同情况，可以进一步将inductive transfer learning分为两种情况：

• 源域中大量已标注数据可用。这种情况下推导迁移学习和多任务学习类似。然而，推导迁移学习只关注于通过从源任务中迁移知识以便在目标任务中获得更高性能，然而多任务学习尝试同时学习源任务和目标任务。
• 源域中无已标注数据可用。这种情况下推导迁移学习和自我学习相似。自我学习中，源域和目标域间的标签空间可能不同，这意味着源域中的边缘信息不能直接使用。因此当源域中无已标注数据可用时这两种学习方法相似。

2. 转导迁移学习（transductive transfer learning）(又叫直推式迁移学习)
   源任务和目标任务相同，源域和目标域不同。这种情况下，目标域中无已标注数据可用，源域中有大量已标注数据可用。除此之外，根据源域和目标域中的不同状况，可以进一步将转导迁移学习分为两类：

• 源域和目标域中的特征空间不同，即\(\mathcal{X}_S\)≠\(\mathcal{X}_T\)；
• 源域和目标域间的特征空间相同，\(\mathcal{X}_S\)=\(\mathcal{X}_T\)，但输入数据的边缘概率分布不同，即\(P(X_S)\)≠\(P(X_T)\).
  转导迁移学习中的后一种情况与自适应学习相关，因为文本分类、样本选择偏差和协方差移位中的知识迁移都有相似的假设。

3. 无监督迁移学习（unsupervised transfer learning）
   与推导迁移学习相似，目标任务与源任务不同但相关。然而，无监督迁移学习专注于解决目标域中的无监督学习问题，如聚类、降维、密度估计。这种情况下，训练中源域和目标域都无已标注数据可用。
   迁移学习中不同分类的联系及相关领域被总结在Table2和Fig2中。
   

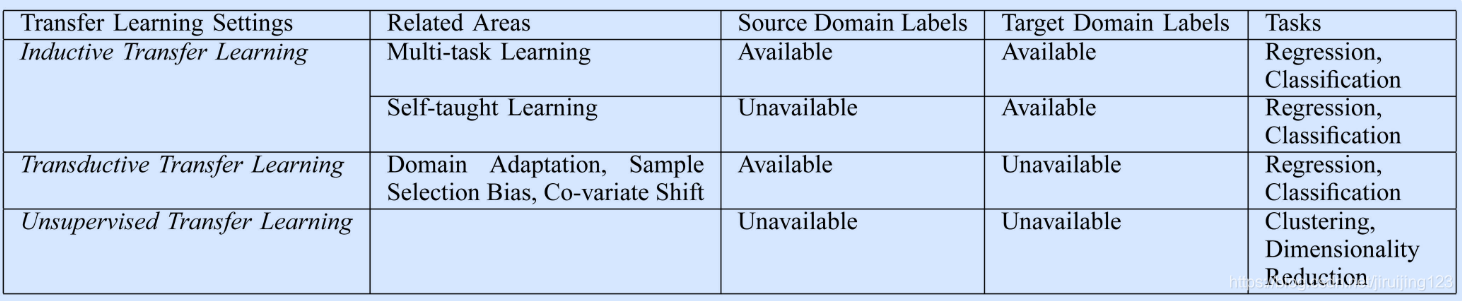
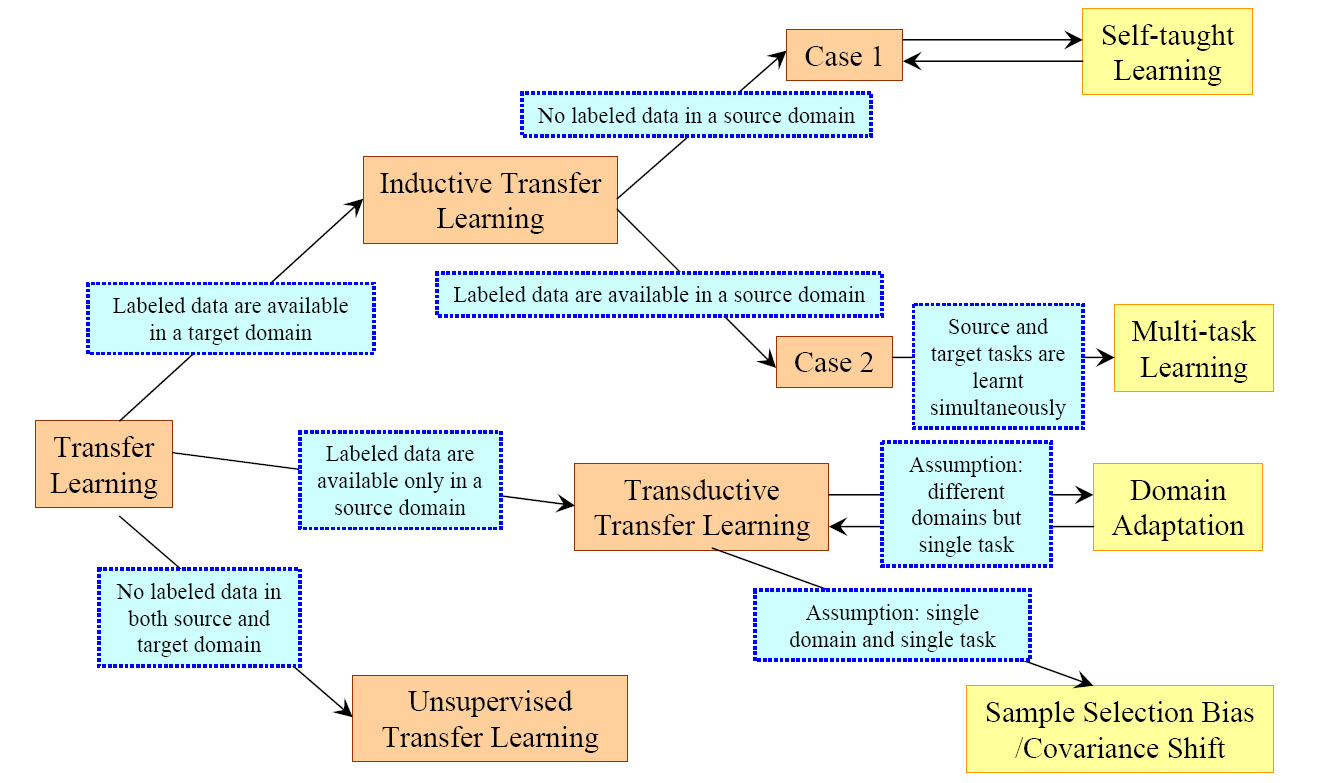
Fig. 2. An Overview of Different Settings of Transfer
  上述三种迁移学习可以基于“迁移什么”被分为四种情况，如Table3所示。Table3中展示了四种情况和简短的描述。

第一种可以被称为基于实例的迁移学习，源域中的数据的某一部分可以通过权重调整的方法重用，用于目标域的学习。实例权重调整和重要性采样是这种方法的两种主要技术。
第二种可以被称为基于特征表示的迁移学习，这种情况的直观想法是为目标域训练一个“好”的特征表示。在这种情况下,用于跨域传输的知识被编码为学习的特征表示形式。使用新功能表示形式,目标任务的性能有望显著提高。第三种情况可称为基于参数的迁移学习方法。这种方法假设假定源任务和目标任务共享模型的超参数的某些参数或先前的超参数分布。最后一种方法可称作关系知识迁移学习（Transferring Relational Knowledge
）问题，它处理的是有联系的域。其基本假设是源域和目标域中某些数据之间关系是相似的。所以要迁移的是数据间的关系。最近，统计关系学习技术主导了这一领域。
表4展示了不同迁移学习分类中不同方法的使用情况。我们可以看到，许多研究工作研究了推导迁移学习而无监督迁移学习是一个相当新的研究话题，而且在上下文中只使用基于特征表示的迁移学习方法对其进行了研究。而且基于特征表示的迁移学习问题在三类迁移学习中都被提及。然而，基于参数的迁移学习和关系知识迁移学习方只在推导迁移学习中研究过，我们将在下面详细讨论推导迁移学习。

3.推导迁移学习

定义：给出一个源域\(\mathcal{D}_S\)和源任务\(\mathcal{T}_S\)，目标域\(\mathcal{D}_T\)目标任务\(\mathcal{T}_T\) ，推导迁移学习的目标是在\(\mathcal{T}_S\)≠\(\mathcal{T}_T\)的情况下，利用\(\mathcal{D}_S\)和\(\mathcal{T}_S\)的知识，帮助提升\(\mathcal{D}_T\) 中的目标预测函数 \(f_T(\cdot)\)。
基于以上的推导迁移学习的定义，用目标域中一小部分已标注数据作为训练数据以诱导（induce）目标预测函数是有必要的。在2.3部分提到，这种分类包含两种情况：（1）源域中标注数据可得到；（2）源域中已标注数据不可得，未标注数据可得。这一分类下大多数迁移学习方法聚焦在前一种情况。

3.1迁移实例知识

推导迁移学习中基于实例的迁移学习方法直观上很有吸引力：尽管源域数据不能直接重用，但还是有一部分特定数据可以和目标域中的一些已标注数据实现重用。
Dai等人为解决推导迁移学习问题提出了一个增强算法TrAdaBoost,它是AdaBoost算法的一个扩展，TrAdaBoost算法假设源域和目标域数据使用相同的特征集和标签集，但两个域中的数据分布不同。除此之外，因为源域和目标域的分布不同，因此TrAdaBoost进一步假设源域中的部分数据对目标域的学习有用，另一部分数据没用甚至有害。它尝试对源域数据迭代式地重加权以减轻坏的源域数据对目标域的影响，增强好数据的增益。迭代的每一轮，TrAdaBoost在加权过的源数据和目标数据上训练基本分类器。只在目标数据上计算错误。TrAdaBoost在更新目标域上的错误分类样例上和AdaBoost使用相同策略，在更新源域上的错误分类源样例上和AdaBoost使用不同策略。TrAdaBoost的具体理论分析见[6]。 Jiang and Zhai
30]提出了一种基于不同条件概率\(P\left(y_{T} | x_{T}\right)\),和\(P\left(y_{S} | x_{S}\right)\)的从源域中移除误导性训练样例的启发式方法。liao等人[31]提出了一种新的主动学习方法,借助源域数据进行标记来选择目标域中的未标记数据。Wu and Dietterich [53]集成源域(辅助)数据支持向量机 (SVM) 框架,以提高分类性能。

3.2转移特征表示的知识

推导迁移学习的基于特征表示的迁移方法致力于找到好的特征表示去最小化域差异以及分类和回归模型误差。不同类型的源数据有找好特征表示的不同策略。如果源域中大量已标注数据可用，有监督方式可以被用于构建特征表示。这有点像多任务学习中的共性特征学习。如果源域中没有已标注数据可用，就要使用无监督方式去构建特征表示。

3.2.1 有监督特征构建

推导迁移学习中的有监督特征构建与多任务学习中使用的方法类似。基本想法是去构建一个可以跨相关任务的低维表示，而且学习到的新表示也可以用于减小每个任务的分类或回归误差。Argyriou et al. [40]提出了一种针对多任务学习的稀疏特征学习方法。在推导迁移学习中，可以通过一个优化问题来学习公共特征，见下式：

\[\underset{A, U}{\arg \min } \sum_{t \in\{T, S\}} \sum_{i=1}^{n_{t}} L\left(y_{t_{i}},\left\langle a_{t}, U^{T} x_{t_{i}}\right\rangle\right)+\gamma\|A\|_{2,1}^{2}\\ \ s.t.\quad U \in \mathbf{O}^{d}\tag{1} \]

\(S\) 和\(T\)表示源域和目标域中的任务，\(A=[a_S,a_T]∈R^{d×2}\)是参数矩阵。\(U\)是一个\(d×d\)的正交矩阵（映射函数）用于将高维数据映射成为低维表示。A的\((r,p)\)范数为\(\|A\|_{r, p} :=\left(\sum_{i=1}^{d}\left\|a^{i}\right\|_{r}^{p}\right)^{\frac{1}{p}}\)。上式表达的优化问题同时估计了低维表示\(U^TX_T, U^TX_S\)和模型的参数\(A\)，上式也可被等效转化为凸优化函数并被高效地解决。 后续工作中，Argyriou et al. [41]提出了一种用于多任务结构学习的光谱正则化框架。
Lee等人[42]提出了一个凸优化算法,用于同时从一系列相关的预测任务中学习元序（metapriors）和特征权重。元序（metapriors）可以在不同的任务之间迁移。Jebara [43] 建议使用 SVM 选择特征进行多任务学习。Ru¨ ckert and Kramer [54]为推导迁移学习设计了一种基于内核的方法,旨在为目标数据找到合适的内核。

3.2.2 无监督特征构建

[22]提出以应用稀疏编码，它是一种无监督特征构建方法，在迁移学习中学习高维特征。这种想法基本由两部构成：第一步，通过在源域数据上求解(2)式得到更高层的偏置向量\(b=\{b1,b2,...,bS\}\)：

\[\min _{a, b} \sum_{i}\left\|x_{S_{i}}-\sum_{j} a_{S_{i}}^{j} b_{j}\right\|_{2}^{2}+\beta\left\|a_{S_{i}}\right\|_{1}\\ s.t.\quad\left\|b_{j}\right\|_{2} \leq 1, \quad \forall j \in 1, \ldots, s \tag{2}\]

在这一等式中\(a_{S_{i}}^{j}\)是一种新的基础表示形式，输入\(x_{S_{i}}\)和\(\beta\)是平衡特征构造项的系数和正则化项系数，得到偏置向量b之后，第二步在目标域数据上应用(3)式以学习基于偏置向量b的更高维特征

\[a_{T_{i}}^{*}=\underset{a_{T_{i}}}{\arg \min }\left\|x_{T_{i}}-\sum_{j} a_{T_{i}}^{j} b_{j}\right\|_{2}^{2}+\beta\left\|a_{T_{i}}\right\|_{1}. \tag{3} \]

最后,可以将鉴别算法应用于\(\{a_{T_{i}}^{*}\}'s\),并带有相应的标签,以用于目标域训练分类或回归模型。此方法的一个缺点是,在优化问题 (2) 中在源域上学习的所谓较高级别基础向量可能不适合在目标域中使用。
最近,多种学习方法被改编成转移学习。在[44]中,Wang和Mahadevan提出了一种基于普鲁克分析的方法,用于无对应的歧管对齐,该方法可用于通过对齐歧管跨领域迁移知识。

3.3 Transferring Knowledge of Parameters

大多数推导迁移学习的基于参数的迁移方法都假设相关任务的不同模型之间共享一些参数或更高层的超参数分布。这部分描述的大多数方法包括一个规则化框架一个多层贝叶斯框架，都被设计在多任务学习下工作。然而，它们可以很容易地为迁移学习修改。就像之前提到的，多任务学习试图同时完美地学习源任务和目标任务，而迁移学习只想利用源域数据提升目标域数据下的性能。因此，多任务学习中对源域和目标域数据的损失函数的权重都一样，而对迁移学习这两者的权重则不同。直观地，我们可以对目标域上的损失函数赋予更高的权重以确保目标域上的效果更好。
Lawrence and Platt[45]提出了一个高效的算法叫MT-IVM，基于高斯过程，以处理多任务学习的情况。MT-IVM试图通过共享相同高斯过程先验参数以在多任务情况下学习高斯过程的参数。Bonilla et al.[46]也在高斯过程情况下调研了多任务学习。作者建议对任务使用自由形式的协方差矩阵来建模任务间依赖关系,其中 高斯过程先验（GP prior）被用于归纳出任务之间的相关性。
除了迁移高斯过程模型的先验信息，一些研究也提出了迁移
正则化框架下SVMs模型的参数。Evgeniou and Pontil[48]在研究多任务学习中SVMs方法借用了HB算法的想法。提出的方法假设对每个任务中SVMs的参数\(w\)可以被分成两个术语。一个是对任务的通用术语，一个是对特殊任务的术语。在推导迁移学习中，

\[w_S=w_0+v_S ,w_T=w_0+v_T \]

其中，\(w_S\)和\(w_T\)分别是源任务和目标学习任务的SVMs算法的参数。\(w_0\)是一个通用参数，\(v_S和v_T\)分别是源任务和目标任务的特殊参数。通过假设\(f_t=w_t\cdot x\)是任务\(t\)的超平面，SVM算法的一个多任务学习方面的扩展可写成如下形式：

\[\begin{array}{l} \underset{w_{0}, v_{t}, \xi_{t_{i}}}{min} J\left(w_{0}, v_{t}, \xi_{t_{i}}\right)\\ =\sum_{t \in\{S, T\}} \sum_{i=1}^{n_{t}} \xi_{t_{i}}+\frac{\lambda_{1}}{2} \sum_{t \in\{S, T\}}\left\|v_{t}\right\|^{2}+\lambda_{2}\left\|w_{0}\right\|^{2}\\ s.t.\quad y_{t_{i}}\left(w_{0}+v_{t}\right) \cdot x_{t_{i}} \geq 1-\xi_{t_{i}}\\ \xi_{t_{i}} \geq 0, i \in\left\{1,2, \ldots, n_{t}\right\} \text { and } t \in\{S, T\}\tag{4} \end{array} \]

通过解决上面的优化问题，我们可以同时学习到参数\(w_0,v_S和v_T\)。Gao et al. [49]提出了一个本地加权集合学习框架,以组合多个用于迁移学习的模型,其中权重根据模型在目标域中每个测试示例上的预测能力动态分配。

3.4 关系知识迁移学习

不同于以上三种方法，关系知识迁移学习方法在关系域中处理迁移学习问题，其数据分布不同且可以被多种关系表示，例如网络关系和社会网络关系。此方法并不假定从每个域中提取的数据是独立且与传统上假定的分布相同。它尝试着把数据联系从源域迁移到目标域，在此背景下,提出了统计关系学习技术来解决这些问题。
Mihalkova等人提出了一种算法TAMAR,该算法将关系知识通过马尔科夫逻辑网络(MLNs)跨关系域迁移。MLNs [56] 是一种强大的形式体系,它结合了一阶逻辑的简洁表现力和概率的灵活性,用于统计关系学习。在 MLNs 中,关系域中的实体由谓词表示,其关系以一阶逻辑表示。TAMAR 的动机是,如果两个域彼此相关,则可能存在映射,将实体及其关系从源域连接到目标域。例如,教授在学术领域扮演的角色,在工业管理领域担任管理者所扮演的角色相似。此外,教授与学生之间的关系与管理者与员工之间的关系相似。因此,可能存在从教授到经理的映射,以及从教授-学生关系到经理-工人关系的映射。在此方面,TAMAR 尝试使用源域学习的 MLN 来帮助学习目标域的 MLN。基本上,TAMAR 是一个两阶段算法。在第一步中,基于加权伪日志可能性度量 (WPLL) 从源 MLN 构造到目标域的映射。在第二步中,通过FORTE算法[57]对目标域中的映射结构进行修订,该算法是一种用于修正一阶理论的归纳逻辑编程(ILP)算法。修订后的 MLN 可用作目标域中推理或原因的关系模型。
在AAAI-2008复杂任务转移学习研讨会上,Mihalkova and Mooney[51]扩展TAMAR到以单实体为中心的迁移学习,其中目标域中只有一个实体可用。Davis and Domingos[52]提出了一种基于二阶马尔科夫逻辑转移关系知识的方法。该算法的基本思想是,通过实例化这些公式与目标域中的谓词,以带有谓词变量的马尔科夫逻辑公式的形式发现源域中的结构规律。

4 转导迁移学习

转导迁移学习话题的是Arnold et al. [58]提出的，他们要求源任务和目标任务相同，尽管域可能不同。除了这些条件之外,他们进一步要求目标域中的所有未标记数据在训练时都可用,但我们相信这种情况可以放宽;相反,在我们定义转导迁移学习时,我们仅要求在训练时查看部分未标记的目标数据,以便获得目标数据的边际概率。
请注意,"转导"一词具有多种含义。在传统的机器学习环境中,转导式学习 [59] 是指在训练时需要查看所有测试数据,并且所学模型不能用于将来数据的情况。因此,当一些新的测试数据到达时,它们必须与所有现有数据一起分类。相反,在转移学习的分类中,我们使用"转导"一词来强调这样一个概念,即在这种类型的转移学习中,任务必须相同,并且目标域中必须有一些未标记的数据。

转导迁移学习定义：

给定源域\(\mathcal{D}_S\)和相应的学习任务\(\mathcal{T}_S\)、目标域 \(\mathcal{D}_T\)和相应的学习任务 \(\mathcal{T}_T\),转导迁移学习旨在利用 \(\mathcal{D}_S\) 和 \(\mathcal{T}_S\)中的知识,改进目标预测函数\(f_T(\cdot)\)的学习,其中 \(\mathcal{D}_S\)≠\(\mathcal{D}_T\) 和 \(\mathcal{T}_S\)=\(\mathcal{T}_T\)。此外,某些未标记的目标域数据必须在训练时可用。

  这一定义涵盖Arnold等人的工作[58],因为后者考虑了领域适应,其中来源数据和目标数据的边际概率分布之间存在差异;即任务相同,但域不同。
  与传统转导式学习设置类似,后者旨在充分利用未标记的测试数据进行学习,在转换传输学习下的分类方案中,我们还假定给出了一些目标域未标记的数据。在上述转导传输学习定义中,源任务和目标任务相同,这意味着可以通过一些未标记的目标域数据,将源域中学习的预测函数调整到目标域中。如第 2.3 节所述,此分类可以拆分为两种情况:（1）源域和目标域特征空间不同，\(\mathcal{X}_S\)≠\(\mathcal{X}_T\)（2）源域和目标域特征空间相同，\(\mathcal{X}_S\)=\(\mathcal{X}_T\)但是输入数据的边际概率分布不同，\(P(X_S)\)≠\(P(X_T)\).这和自适应学习和样本选择偏差的要求类似。接下来描述的方法都和上面的第二种情况有关。

4.1迁移实例的知识

大多数转导迁移学习的实例迁移方法都受到重要性采样的激励。为了了解基于重要性采样的方法在此环境中如何提供帮助,我们首先回顾了经验风险最小化问题（ERM）[60]。一般来说，我们可能想要经验最小化风险来学习模型最优参数\(\theta^{*}\)

\[\theta^{*}=\underset{\theta \in \Theta}{\arg \min } \mathbb{E}_{(x, y) \in P}[l(x, y, \theta)] \]

其中\(l(x, y, \theta)\)是依赖于参数的损耗函数。但是,由于很难估计概率分布 P,我们选择最小化 ERM,

\[\theta^{*}=\underset{\theta \in \Theta}{\arg \min } \frac{1}{n} \sum_{i=1}^{n}\left[l\left(x_{i}, y_{i}, \theta\right)\right] \]

其中，n是训练数据的size（尺寸）。
在在转导迁移学习中,我们希望通过经验风险最小化来学习目标域的最佳模型,

\[\theta^{*}=\underset{\theta \in \Theta}{\arg \min } \sum_{(x, y) \in D_{T}} P\left(D_{T}\right) l(x, y, \theta) \]

但是,由于在训练数据中未观察到目标域中标记数据,因此我们必须从源域数据中学习模型。如果\(P(D_S)=P(D_T)\),那么我们只需通过解决以下优化问题来了解模型,以便用于目标域,

\[\theta^{*}=\underset{\theta \in \Theta}{\arg \min } \sum_{(x, y) \in D_{S}} P\left(D_{S}\right) l(x, y, \theta) \]

当\(P(D_S)\)≠\(P(D_T)\)时，我们需要调整优化问题，以期为目标域学习一个具有较高概括能力的模型，如下：

\[\begin{aligned} \theta^{*}=\underset{\theta \in \Theta}{\arg \min } \sum_{(x, y) \in D_{S}} \frac{P\left(D_{T}\right)}{P\left(D_{S}\right)} P\left(D_{S}\right) l(x, y, \theta)\\ \approx \underset{\theta \in \Theta}{\arg \min } \sum_{i=1}^{n_{S}} \frac{P_{T}\left(x_{T_{i}}, y_{T_{i}}\right)}{P_{S}\left(x_{S_{i}}, y_{S_{i}}\right)} l\left(x_{S_{i}}, y_{S_{i}}, \theta\right). \end{aligned}\tag{5} \]

因此,通过相应的权重\(\frac{P_{T}\left(x_{T_{i}}, y_{T_{i}}\right)}{P_{S}\left(x_{S_{i}}, y_{S_{i}}\right)}\)为每个实例添加不同的惩罚值\((x_{S_{i}},y_{S_{i}},)\),我们可以使用相应的权重来学习目标域的精确模型。而且，因为\(P\left(Y_{T} | X_{T}\right)=P\left(Y_{S} | X_{S}\right)\)，所以\(P(D_S)\)和\(P(D_T)\)的不同主要又\(P(X_S)\)和\(P(X_T)\)造成，且

\[\frac{P_{T}\left(x_{T_{i}}, y_{T_{i}}\right)}{P_{S}\left(x_{S_{i}}, y_{S_{i}}\right)}=\frac{P\left(x_{S_{i}}\right)}{P\left(x_{T_{i}}\right)} \]

如果我们可以为每个实例预测\(\frac{P\left(x_{S_{i}}\right)}{P\left(x_{T_{i}}\right)}\)，我们就可以解决转导迁移学习问题。
有多种预测 \(\frac{P\left(x_{S_{i}}\right)}{P\left(x_{T_{i}}\right)}\)的方法。Zadrozny [24]提出构建简单的分类问题来估计\(P\left(x_{S_{i}}\right)\)和\(P\left(x_{T_{i}}\right)\)。Fan等人[35]使用各种分类器对问题进行了进一步分析,估计了概率比。Huang等人[32]提出了一种内核均值匹配(KMM)算法,通过匹配在复制内核Hilbert空间(RKHS)中学习源域数据和目标域数据的方法算法来直接学习\(\frac{P\left(x_{S_{i}}\right)}{P\left(x_{T_{i}}\right)}\)。KMM 可以重写为以下二次编程 (QP) 优化问题。

\[\begin{array} {ll}{\min _{\beta}} & {\frac{1}{2} \beta^{T} K \beta-\kappa^{T} \beta} \\ {\text {s.t.}} & {\beta_{i} \in[0, B] \text { and }\left|\sum_{i=1}^{n_{S}} \beta_{i}-n_{S}\right| \leq n_{S} \epsilon}\tag{6} \end{array} \]

其中$$
K=\left[\begin{array}{ll}{K_{S, S}} & {K_{S, T}} \ {K_{T, S}} & {K_{T, T}}\end{array}\right]

\[$K_{i j}=k\left(x_{i}, x_{j}\right)$$K_{S, S}$ 和 $K_{T, T}$是源域和目标域数据的核矩阵。$\kappa_{i}=\frac{n_{S}}{n_{T}} \sum_{j=1}^{n_{T}} k\left(x_{i}, x_{T_{j}}\right)$其中，$x_{i} \in X_{S} \cup X_{T}$$x_{T_{j}} \in X_{T}$。 可证明：$\beta_{i}=\frac{P\left(x_{S_{i}}\right)}{P\left(x_{T_{i}}\right)}$[32]。使用KMM的优点在于避免计算$P(x_{S_{i}})$或$P(x_{T_{i}})$的密度估计，当数据集小的时候很难计算。Sugiyama等人[34]提出了一种称为"库尔贝克-莱布勒重要性估计步骤(KLIEP)"的算法,以在最小化Kullback-Lebler不同的基础上直接估计$\frac{P\left(x_{S_{i}}\right)}{P\left(x_{T_{i}}\right)}$。可以集成交叉验证,通过两个步骤自动执行模型选择:1) 估计源域数据的权重,2) 在重加权数据上训练模型。Bickel等人[33]通过派生一个内核逻辑回归分类器,将两个步骤合并为一个统一的框架。有关协变量移位或样本选择偏差的重要性采样和重量化方法的更多信息,读者可以参考 Quionero-Candela 等人最近出版的一本书 [29]。也可以参考ICDM-08中fan和Sugiyama的样本选择偏差教程。 ## 4.2迁移特征表示的知识 转导迁移学习的大多数特征表示迁移方法都在无监督的学习框架之下。Blitzer等人[38]提出了一种结构对应学习(SCL)算法,该算法扩展了[37],利用目标域中的未标记数据提取一些相关特征,这些特征可以缩小域之间的差异。SCL算法的第一步是在两个域的无标注数据中定义一组枢轴特征（数轴的特征数量由$m$表示）。然后SCL 从数据中删除这些枢轴特征,并将每个枢轴要素视为新的标注矢量。可以构造 m 分类问题。假设每个分类可以通过线性分类器解决，线性分类器如下： \]

f_{l}(x)=\operatorname{sgn}\left(w_{l}^{T} \cdot x\right), l=1, \ldots, m

\[SCL能够学到一个参数矩阵$W=\left[w_{1} w_{2} \dots w_{m}\right]$。第三步，奇异值分解 (SVD) 应用于矩阵$W=\left[w_{1} w_{2} \dots w_{m}\right]$ 使得$W=U D V^{T},$ 于是，$\theta=U_{[1 ! h ;]}^{T}$是矩阵(线性映射),其行是 W 的左上单数矢量。$h$是共享特征的数量。最后,标准判别算法可以应用于增强特征向量来构建模型。增强特征矢量包含所有原始要素$x_i$,并附加了新的共享要素$\theta x_i$。如 [38] 中所述,如果枢轴特征设计的好,则学习的映射将编码不同域中的要素之间的对应关系。虽然Ben-David 等人[61]实验表明,SCL可以减少域之间的差异;如何选择枢轴特征是困难的,并且依赖于域。在[38]中,Blitzer等人使用启发式方法为自然语言处理(NLP)问题选择枢轴特征,例如句子标记。在后续研究中,研究人员建议使用相互信息 (MI) 来选择枢轴特征,而不是使用更多启发式标准 [8]。MI-SCL 尝试寻找一些高度依赖源域中标签的枢轴特征。 NLP 领域中的迁移学习有时称为域适应。在此领域,Daume [39] 提出了针对 NLP 问题的内核映射函数,该函数将数据从源域和目标域映射到高维特征空间,其中使用标准鉴别性学习方法来训练分类器。但是,构建的内核映射函数是域知识驱动的。将内核映射概括为其他领域或应用程序并不容易。Blitzer 等人 [62] 分析了算法的统一收敛边界,这些算法将源和目标经验风险的凸组合降至最低。在[36]中,Dai等人提出了一种基于共聚类的算法,用于在不同的域中传播标签信息。在[63]中,Xing等人提出了一种称为桥接细化（bridged refinement）的新算法,以纠正由转移不感知分类器预测的标签,并将训练和测试数据的混合分布作为桥梁,以更好地从将数据训练到测试数据。在[64]中,Ling等人提出了跨域迁移学习问题的光谱分类框架,其中引入了目标函数,以寻求域内监督与域外内在结构的一致性。在[65]中,薛等人提出了一种跨域文本分类算法,将传统的概率潜在语义分析(PLSA)算法扩展为将不同但相关领域的标记和未标记数据集成到一个统一的概率模型。新模型称为主题桥式 PLSA 或 TPLSA。 潘等人最近提出通过维数减少迁移学习[66]在这项工作中,Pan等人利用了最初为减小维数而设计的最大平均差异嵌入(MMDE)方法,学习低维空间,以减少不同域之间的分布差异,以实现转导迁移学习。但是,MMDE 可能会承受计算负担。因此,在[67]中,Pan等人进一步提出了一种有效的特征提取算法,称为转移分量分析(TCA),以克服MMDE的缺点。 # 5无监督式迁移学习 定义4（无监督迁移学习）：给定一个源域$\mathcal{D}_S$和学习任务 $\mathcal{T}_S$目标域$\mathcal{D}_T$和对应的学习任务$\mathcal{T}_T$无监督迁移学习的目标是使用$\mathcal{D}_S$和目标域$\mathcal{T}_S$的知识，帮助提升目标域中目标预测函数$f_{T}(\cdot)$。其$\mathcal{T}_{S}$≠ $\mathcal{T}_{T}$而且$\mathcal{Y}_S$和$\mathcal{Y}_T$是未标注的。 根据无监督传输学习设置的定义,在培训中的源域和目标域中未观察到标记数据。到目前为止,关于此设置的研究工作很少。最近,分别提出了自学聚类(STC)[26]和迁移判性分析(TDA)[27]算法来迁移聚类和迁移减少维度数问题。 ## 5.1 基于特征表示迁移知识 Dai等人(26)研究了一个新的聚类问题案例,称为自学聚类（STC）。自学聚类是无监督传输学习的实例,它旨在通过源域中的大量未标记数据在目标域中集中少量未标记数据。STC 尝试学习跨域的通用要素空间,这有助于在目标域中进行群集。STC 的目标功能如下所示: $$\begin{aligned} &J\left(\tilde{X}_{T}, \tilde{X}_{S}, \tilde{Z}\right)\\ &\quad=I\left(X_{T}, Z\right)-I\left(\tilde{X}_{T}, \tilde{Z}\right)+\lambda\left[I\left(X_{S}, Z\right)-I\left(\tilde{X}_{S}, \tilde{Z}\right)\right] \end{aligned}\tag{7} \]

其中，\(X_S\)和\(X_T\)是源域和目标域数据。\(Z\)是\(X_S\)和\(X_T\)的标准共享特征空间，\(I(\cdot, \cdot)\)是两个随机变量的共同信息。假设存在三个聚类函数，\(C_{X_{I}} : X_{T} \rightarrow \tilde{X}_{T}, C_{X_{s}} : X_{S} \rightarrow \tilde{X}_{S},\) and \(C_{Z} : Z \rightarrow \tilde{Z}\)。其中
\(\tilde{X}_{T},\tilde{X}_{S}和\tilde{Z}\)对应$X_T,X_S和Z的对应聚类。STC的目标是通过解决最优化问题（7）来学习 \(\tilde{X}_{T}\)：

\[\underset{\tilde{X}_{T}, \vec{X}_{S}, \tilde{Z}}{\arg \min } J\left(\tilde{X}_{T}, \tilde{X}_{S}, \tilde{Z}\right)\tag{8} \]

在 [26] 中给出了一种用于求解优化函数 (8) 的迭代算法。
同样,Wang等人提出了一种TDA算法来解决迁移维数减少问题。TDA 首先应用聚类方法为目标未标记的数据生成伪类标签。然后,它将尺寸减少方法应用于目标数据和有标记的源数据以减少维度。这两个步骤以迭代方式运行,以查找目标数据的最佳子空间。

6迁移边界和负迁移

一个重要的问题是认识到迁移学习的能力的极限。在[68]中,Mahmud和Ray分析了使用柯尔莫戈罗夫复杂性（柯氏复杂度）（kolmogorov complexity）进行迁移学习的案例,其中证明了一些理论界限。特别是,作者使用有条件的柯尔莫戈罗夫复杂性来衡量任务之间的关联度,并在贝叶斯框架下的连续迁移学习任务中传输"正确的"信息量。
最近,伊顿等人提出了一种新的基于图形的知识转移方法,其中源任务之间的关系是通过将学习源模型集嵌入到图形中,使用可转移性作为度量指标来建模的。通过将问题映射到图形,然后学习此图上的函数,该函数自动确定要传输到新学习任务的参数,从而继续迁移到新任务。
  当源域数据和任务导致目标域中学习性能降低时,就会发生负迁移。尽管如何避免负面转移是一个非常重要的问题,但关于这个主题的研究工作很少。Rosenstein等人[70]的经验表明,如果两个任务太不同,那么暴力转移可能会损害目标任务的性能。一些作品已被利用来分析任务和任务聚类技术之间的关联性,例如 [71]、[72],这可能有助于就如何自动避免负转移提供指导。Bakker 和 Heskes [72] 采用了贝叶斯方法,其中一些模型参数对所有任务共享,而其他模型参数通过从数据中学习的联合先前分发更松散地连接。因此,数据基于任务参数进行聚类,其中同一群集中的任务应该彼此相关。Argyriou等人[73]考虑了学习任务可以分为几组的情况。每个组内的任务通过共享低维表示来相关,该表示在不同的组之间有所不同。因此,团队中的任务可以发现更容易迁移有用的知识。

7迁移学习的应用

最近,传输学习技术已成功应用于许多实际应用。Raina等人[74]和Dai等人[36],[28]建议分别使用转移学习技术来学习跨领域的文本数据。Blitzer等人建议使用SCL来解决NLP问题。在[8]中,为解决情绪分类问题,提出了SCL的扩展建议。Wu和Dietterich[53]建议同时使用不足的目标域数据和大量低质量的源域数据来解决图像分类问题。Arnold等人[58]建议采用转导迁移学习方法解决名称实体识别问题。在 [75]、[76]、[77]、[78]、[79]中,提出了迁移学习技术,以从WiFi本地化模型中提取跨时间段、空间和移动设备的知识,为了有助于其他地点的WiFi定位任务。卓等人[80]研究了如何在自动化规划中迁移领域知识,学习跨领域的关系行为模型。
在[81]中,Raykar等人提出了一种新的贝叶斯多实例学习算法,该算法可以自动识别相关特征子集,并使用归纳迁移进行学习多种、但是概念上相关的分类器,用于计算机辅助设计(CAD)。在[82]中,Ling等人提出了一种信息理论方法,用于迁移学习,以解决将网页从英文翻译成中文的跨语言分类问题。当有大量标有标记的英文文本数据而只有少量贴有中文文本文档时,这种方法解决了这个问题。通过设计合适的映射函数作为桥梁,可以实现跨两个特征空间的迁移学习。
到目前为止,至少有两场基于迁移学习的国际比赛,提供了一些急需的公共数据。在 ECML/PKDD-2006 发现挑战中,8 的任务是处理跨相关学习任务的个性化垃圾邮件筛选和概括。为了培训垃圾邮件过滤系统,我们需要从一组带有相应标签的用户收集大量电子邮件:垃圾邮件或非垃圾邮件,并根据这些数据训练分类器。对于新的电子邮件用户,我们可能希望为用户调整学习的模型。挑战在于第一组用户和新用户的电子邮件分发情况不同。因此,这个问题可以模拟为一个归纳传输学习问题,其目的是使旧的垃圾邮件过滤模型适应训练数据少、培训时间少的新情况。
通过ICDM-2007竞赛提供了第二组数据集，其中任务是使用不同时间段获得的WiFi信号数据估计WiFi客户端的室内位置[83]。由于WiFi信号强度值可能是时间、空间和设备的函数，因此不同时间段内WiFi数据的分布可能会非常不同。因此，迁移学习必须设计为减少数据重新标记的工作量。
用于传输学习的数据集。到目前为止,已经发布了几组数据集用于转移学习研究。我们分别表示文本挖掘数据集、电子邮件垃圾邮件过滤数据集、跨时间段数据集的 WiFi 本地化以及文本、电子邮件、WiFi 和 Sen 的"情绪"分类数据集。

1. 文本。三个数据集,20个新闻组,SRAA和路透社-21578,9已经预先处理为转移学习设置由一些研究人员。这些数据集中的数据被分类为层次结构。来自同一父类别下不同子类别的数据被视为来自不同但相关的域。任务是预测父类别的标签。
2. 电子邮件。此数据集由 2006 年 ECML/PKDD 发现挑战提供。
3. WiFi。此数据集由 ICDM-2007 竞赛提供。在两个不同的时间段内，这些数据在145:5 37:5m2左右的建筑物内收集，用于本地化。
4. Sen. 此数据集首次在 [8]11 中使用,此数据集包含从四个产品类型(域)Amazon.com下载的产品评论:厨房、书籍、DVD 和电子。每个域有数千条评论,但具体数量因域而异。评论包含星级(1-5 星)。

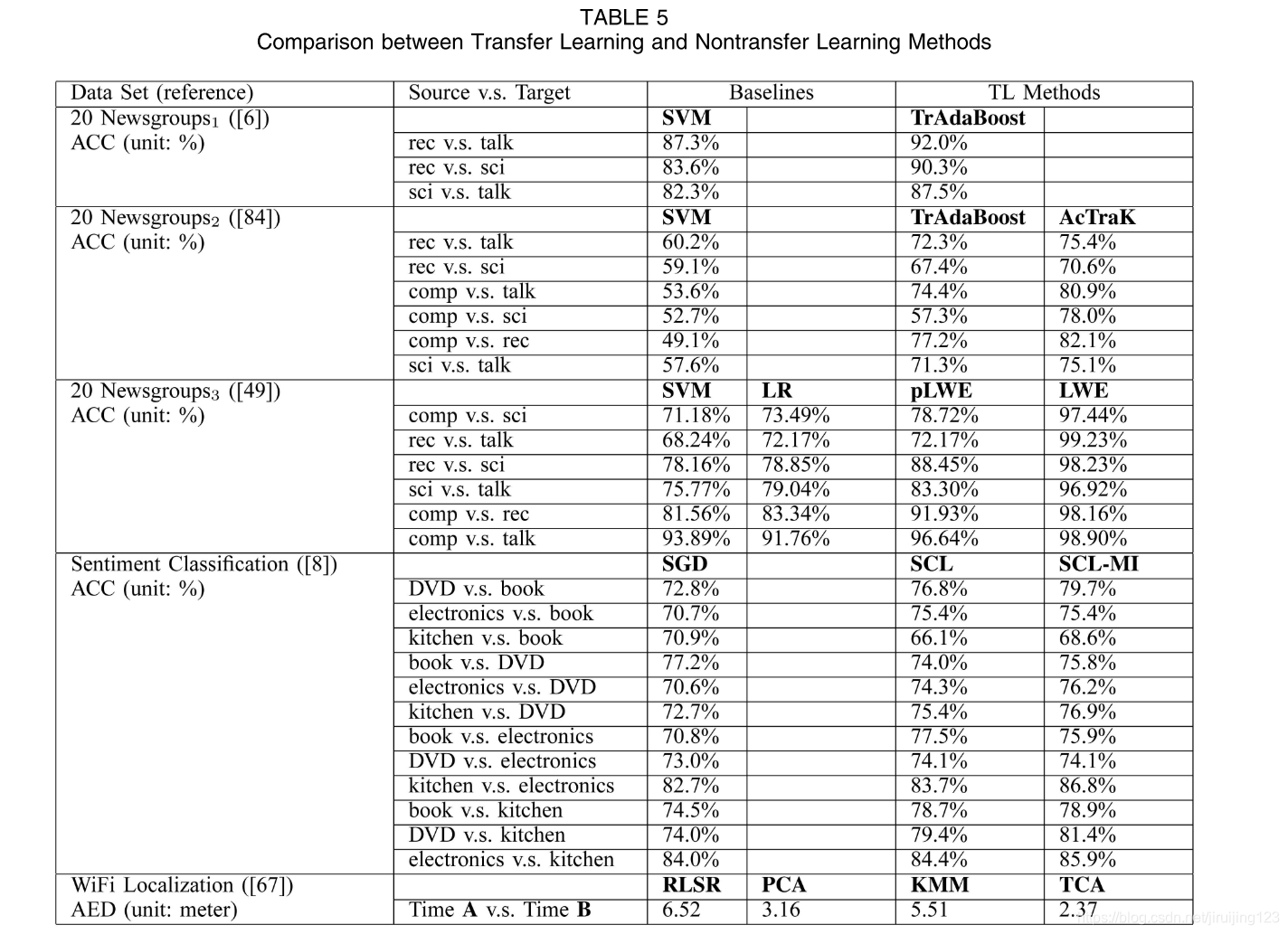
经验评估。为了说明与传统学习方法相比,转移学习方法能带来多大的好处,研究人员使用了一些公共数据集。我们显示了表 5 中一些已发表的转让学习论文的列表。在[6],[84],[49]中,作者使用20个新闻组数据12作为评估数据集之一。由于不同研究者对算法的预处理步骤存在差异,很难直接比较所提出的方法。因此,我们分别用20-News组1、20-News组2和20-News组3来表示它们,并在表中显示建议的转移学习方法和非转移学习方法之间的比较结果。
在20个Newsgroups1数据上,Dai等人[6]展示了标准SVM与建议的TrAdaBoost算法之间的比较实验。在 20 Newsgroups2 上,Shi 等人 [84] 应用了主动学习算法,使用 TrAdaBoost 和标准 SVM 选择转移学习的重要实例 (AcTraK)。Gao等人[49]在20个新闻组3上评估了他们提出的本地加权集合学习算法pLWE和LWE,与SVM和逻辑回归(LR)相比。此外,在表中,我们还显示了 [8] 中报告的情绪分类数据集的比较结果。在此数据集中,SGD 表示具有 Huber 损耗的随机梯度级算法,SCL 表示结构对应学习算法学习的新表示法的线性预测器,SCL-MI 是 SCL 的扩展,通过应用相互用于选择 SCL 算法的透视要素的信息。
最后,在 WiFi 本地化数据集上,我们显示了在 [67] 中报告的比较结果,其中基线是一个规范化的最小平方回归模型 (RLSR),这是一个标准回归模型,KPCA 表示将 RLSR 应用于新的内核原理组件分析所学数据的表示形式。比较的传输学习方法包括KMM和建议的算法TCA。有关实验结果的更多详细信息,读者可以参考表中的参考文献。从这些比较结果中,我们可以发现,与非转移学习方法相比,为实际应用设计得当的转移学习方法确实可以显著提高性能。
用于转移学习的工具箱。 加州大学伯克利分校的研究人员提供了用于传输学习的MATLAB工具包。而且，它提供了一个标准的用于开发和测试传输学习新算法的平台。

7.1迁移学习的其他应用

  传输学习在连续机器学习中也有许多应用。例如,Kuhlmann 和 Stone [85] 提出了一种基于图形的方法来识别以前遇到的游戏,并应用此技术自动绘制值函数传输的域映射,并加快对以前变体的强化学习玩游戏。翻译学习中提出了一种在完全不同的特征空间之间传输的新方法,通过学习映射函数来桥接两个完全不同的域(图像和文本)中的特征[86]。最后,Li等人[87],[88]将迁移学习应用于协同过滤问题,以解决冷启动和稀疏问题。在[87]中,Li等人从潜在的用户和项目群集变量的角度学习了一个共享评级模式混合模型,称为评级矩阵生成模型(RMGM)。RMGM 通过将每个评级矩阵中的用户和项目映射到共享的潜在用户和项目空间来桥接来自不同域的多个评级矩阵,以便传输有用的知识。在[88]中,他们在辅助评级矩阵中对用户和项目应用了共聚类算法。然后,他们构建了一个称为代码手册的群集级评级矩阵。通过假设目标评级矩阵(在电影中)与辅助矩阵(在书籍上)相关,可以通过扩展代码手册、完成知识转移过程来重建目标域。

8结论

  在本综述中,我们回顾了迁移学习的几种当前趋势。迁移学习分为三种不同的设置:推导迁移学习、转导迁移学习和非监督转移学习。前面的大多数作品都集中在前两个分类上。无监督迁移学习将来可能会吸引越来越多的关注。
  此外,每种方法的迁移学习可以基于"迁移什么"在学习分为四个分类。它们分别包括实例转移方法、特征表示迁移方法、参数迁移方法和关系知识迁移方法。前三个上下文对数据有一个\(i.i.d\). 假设,而最后一个上下文处理关系数据的迁移学习。这些方法大多假定所选源域与目标域相关。
  今后需要解决若干重要的研究问题。首先,如何避免负迁移是一个悬而未决的问题。如第 6 节所述,许多建议的迁移学习算法假定源域和目标域在某种意义上是相互关联的。但是,如果假设不成立,则可能发生负转移,这可能导致迁移学习的表现比根本不转移差。因此,如何确保不发生负迁移是迁移学习中的一个关键问题。为了避免负转移学习,我们需要首先研究源域或任务与目标域或任务之间的可迁移性。然后,根据适当的可迁移性措施,我们可以选择相关的源域或任务,以提取知识以学习目标任务。要定义域和任务之间的可迁移性,我们还需要定义测量域或任务之间的相似性的标准。根据距离度量,我们可以对域或任务进行分组,这可能有助于测量可转移性。一个相关的问题是,当整个域不能用于传输学习时,我们是否仍然可以转移部分域,以便在目标域中进行有用的学习。
  此外,到目前为止,大多数现有的迁移学习算法都侧重于改进源域和目标域或任务之间不同分布的通用化。在此过程中,他们假定源域和目标域之间的特征空间相同。但是,在许多应用程序中,我们可能希望跨具有不同特征空间的域或任务迁移知识,并从多个此类源域迁移知识。我们将这种类型的迁移学习称为异构迁移学习。
  最后,到目前为止,迁移学习技术已主要应用于种类有限的小规模应用,如基于传感器网络的本地化、文本分类和图像分类问题。将来,迁移学习技术将广泛用于解决其他具有挑战性的应用,如视频分类、社交网络分析和逻辑推理。

致谢

作者感谢香港CERG项目621307的支持和NEC中国实验室的赠款。

参考：

1.庄福振,罗平,何清,史忠植.迁移学习研究进展.软件 学报,2015,26(1):26-39. http://www.jos.org.cn/1000-9825/4631.htm
2. 论文原文（没想到还有彩色版的）http://citeseer.ist.psu.edu/viewdoc/download?doi=10.1.1.147.9185&rep=rep1&type=pdf
3. https://blog.csdn.net/magic_leg/article/details/73957331