宏观经济学(1-4)
国民经济核算
交易不改变 GDP,除非收手续费
储蓄减投资等于预算赤字减贸易赤字
二手货的出售不计入当期 GDP,因为在其生产的时候已计入 GDP,当期只是资产的转移而非收入增加。当期变质存货的不计入,但以后销售的计入。
NNP = GNP - 折旧
PCE(个人消费支出)平减指数的特征是 CPI 与 GDP 平减指数的混合,只包含消费者购买产品和服务的价格,因此包含进口品的价格;又给不同产品分配变动的权重。
失业率 = 失业者 / ( 失业者 + 就业者 )
劳动力参与率 = ( 失业者 + 就业者 ) / ( 成年人 )(成年人包括不属于劳动者的人)
索洛模型(新古典增长模型,外生增长模型)
生产函数
规模报酬不变, 与
无关:
竞争性经济中, ,
为常量:
其中 和
分别为劳动者报酬和资本所得占 GDP 份额,
为常数,由此便可知
。
因为
为全要素生产率的增长率。在增长核算中,是由
得到
,称为索洛剩余。
全要素生产率不仅仅是技术,也有人力资本等因素。但在下文,只考虑技术,并只考虑技术为劳动增进型 ,即技术进步不改产出与资本之间的关系。显然此处
的内涵发生了变化。可以推出
或
。
假定产出是资本与有效劳动 的一次齐次函数,则有效劳动的人均产出
其中
。
稳态定义为 ,于是
。由于边际产量递减,此方程一定有非零解。由于方程所有量均不含时间,所以方程的解
为关于时间的常数,由此可知
亦为常数。于是稳态增长率
,
,
。
下面考虑储蓄率的影响。人均消费最大时,居民的福利最好。这要求 ,称为黄金法则。稳态不一定符合黄金法则。当符合时,解微分方程,
,
为常数。储蓄率对人均产量、消费和投资的影响如下。
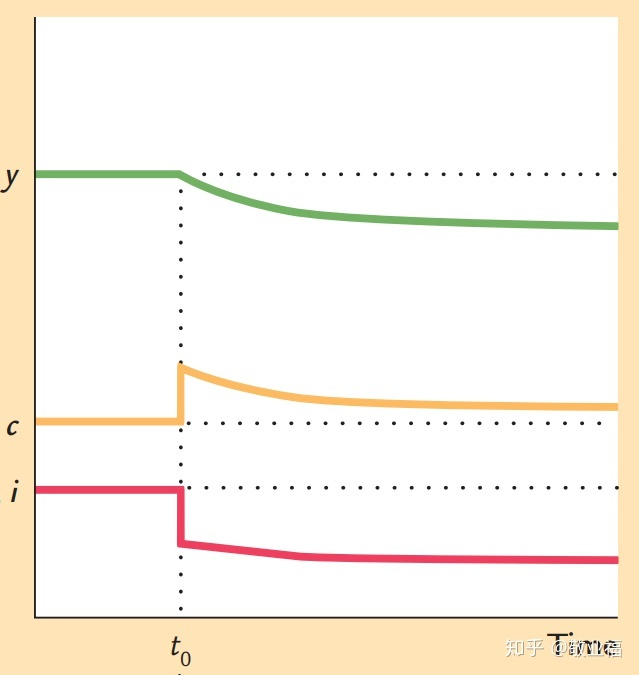
初始条件人均资本大于黄金律水平
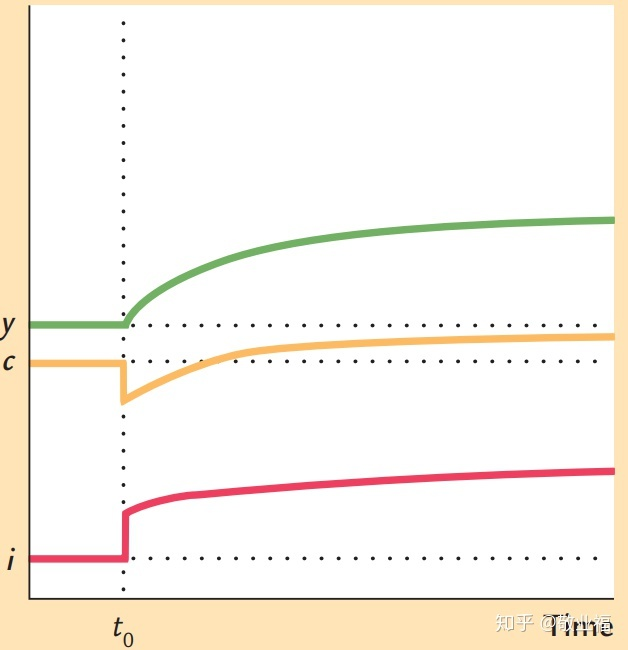
初始条件人均资本小于黄金律水平
内生增长理论
索洛模型中,长期增长率只取决于人口增长和技术进步,政策无法改变增长率。特别是,储蓄率有水平效应,其增长效应只是暂时的。这当中最根本的原因是边际产量递减。现去除此假定,认为资本的边际产量不变,那么规模报酬递增。这是因为保持劳动力不变,资本翻番就会使得产量翻番;现在劳动力也翻番,那么总的效果就是产量不止是翻番。但是,规模报酬递增难道不会导致世界上只剩下一个垄断厂家吗?答案是不会。因为这里的“报酬”还包括了易于“外溢”的技术进步,也就是说报酬并不是由单个厂家私人独占的,因此也就不会形成垄断。这个模型中,技术进步不再是外生的,而是包含在边际产量不变的假设之中。
只要 ,经济就一直增长。特别是,提高储蓄率,有助于提高增长率。然而,经验证据对此支持不足。
两个增长模型的不同还表现在:索洛模型中人口增长率对人均产量增长率无影响,只影响人均产量水平,而内生增长理论中降低人口增长率可以提高人均产量增长率,;索洛模型可以解释观察到的条件趋同,但内生增长理论不能解释国际差异。
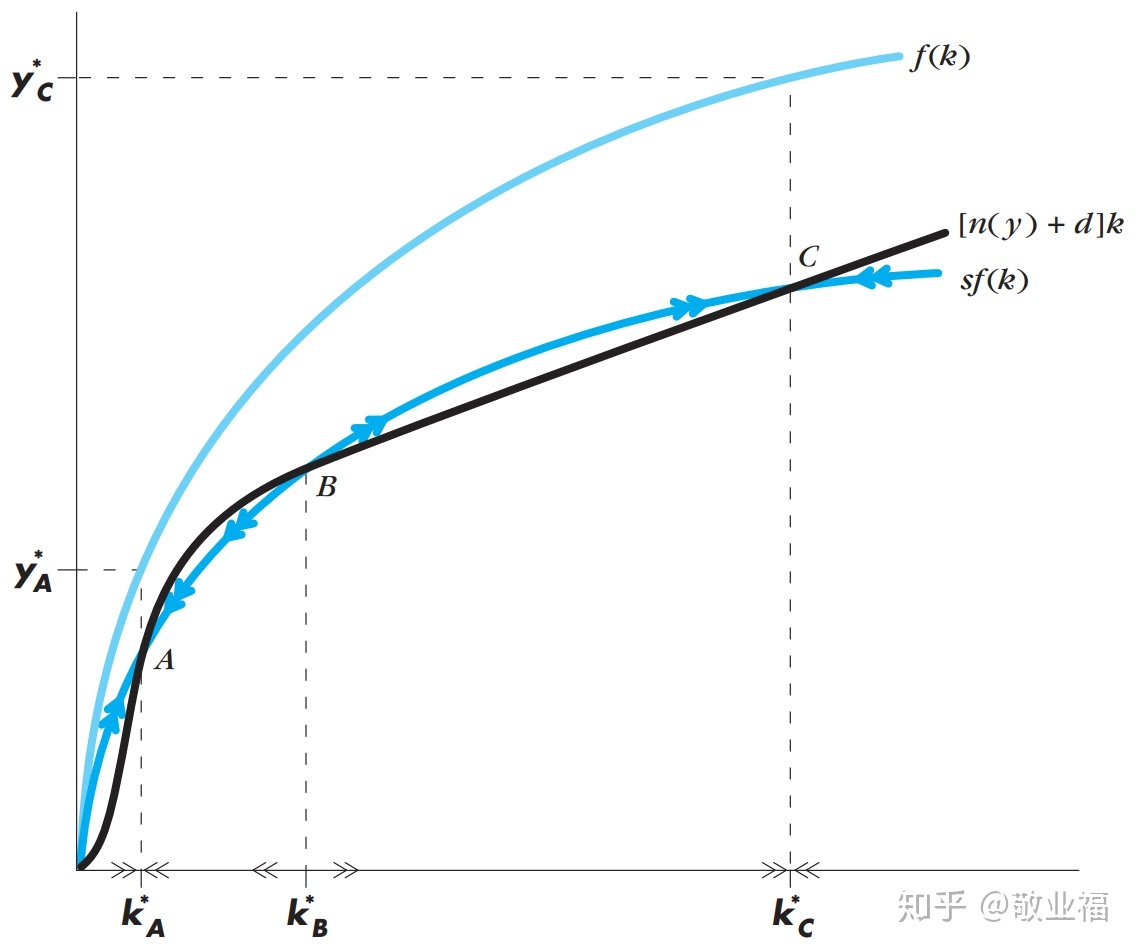
降低人口增长率有助于避免贫困陷阱(B)
总结:对于 、
、
,索洛模型——水平效应而无增长效应;内生增长理论——增长效应而无水平效应。



