快速幂法

1.剑指offer16:数值的整数次方。

实现函数double Power(double base, int exponent)，求base的exponent次方。不得使用库函数，同时不需要考虑大数问题。

说明：

• -100.0 < x < 100.0
• n 是 32 位有符号整数，其数值范围是 [−2³¹, 2³¹ − 1] 。

https://leetcode-cn.com/problems/shu-zhi-de-zheng-shu-ci-fang-lcof/

class Solution {
    public double myPow(double x, int n) {
        
        long d = n;
        double res = 1.0;
        if(n<0){
            x = 1/x;
            d = -d;
        }
        while(d>0){
            if((d&1)==1)res = res*x;
            x = x*x;
            d = d>>1;
        }
        return res;

        // if(n==0)return 1;
        // if(n<0){
        //     return 1/x*myPow(1/x,-n-1);
        // }
        // return n%2==0? myPow(x*x,n/2):x*myPow(x*x,n/2);
    }
}

解：

指数n可能为负数，取相反数时可能会发生溢出，如  -2^31 取 相反数为2^31 而int的范围为 [−2³¹, 2³¹ − 1] ，所以发生溢出。

所以声明一个long类型的变量 long d  = n;防止溢出。

将指数n拆解为二进制的展开式。

如9 的二进制为 1001；

 

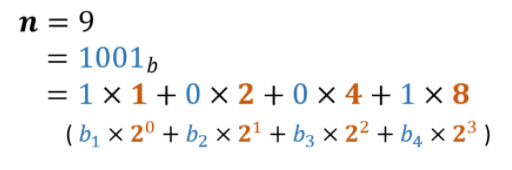
 那么：

 

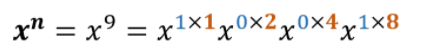
 可以发现当二进制的某一位为0时，就相当于乘了一个x^0==1. 所以为0时不需要对res变量进行操作，只需要考虑二进制位为1的时候对res进行操作（另外因为x^2 = x*x; x^4 = x^2*x^2……,所以每经过一个循环都要执行x = x*x 操作）

所以我们先声明一个变量res = 1，然后从右向左遍历指数n的二进制中的每一位，当这一位为0时 不对res进行操作，只对x进行操作，另x = x*x;然后指数n的二进制向右移位。当这一位为1时，我们另res = res*x;，然后对x进行操作，在然后对指数n进行移位，直到n==0结束。最终返回res结果变量。