树的同构

7-1 树的同构 (30 point(s))

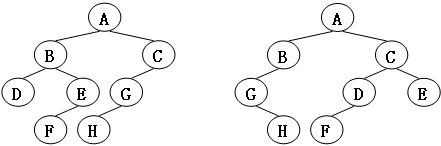
给定两棵树T1和T2。如果T1可以通过若干次左右孩子互换就变成T2，则我们称两棵树是“同构”的。例如图1给出的两棵树就是同构的，因为我们把其中一棵树的结点A、B、G的左右孩子互换后，就得到另外一棵树。而图2就不是同构的。

 

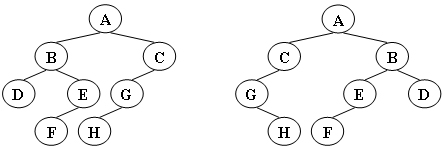
图1

图2

现给定两棵树，请你判断它们是否是同构的。

输入格式:

输入给出2棵二叉树树的信息。对于每棵树，首先在一行中给出一个非负整数N (≤)，即该树的结点数（此时假设结点从0到N−1编号）；随后N行，第i行对应编号第i个结点，给出该结点中存储的1个英文大写字母、其左孩子结点的编号、右孩子结点的编号。如果孩子结点为空，则在相应位置上给出“-”。给出的数据间用一个空格分隔。注意：题目保证每个结点中存储的字母是不同的。

 

先从大的框架主函数写起，先不管怎么实现先大胆用各种函数

方法：先建立两棵树并返回根结点，再判断返回结果，根据结果输出yes或no

int main()
{
    int root1,root2;
    root1=input(t1);  //接收数据生成一棵树并返回根结点的标号 
    root2=input(t2);
    if(match(root1,root2)) //调用函数返回判断结果 
       cout<<"Yes";
    else 
       cout<<"No";
       return 0;   
}

先把结点的定义确定下来

方法：字符型的数据，整型的左右孩子

typedef struct
{
    char data;
    int lchild,rchild;
}node;  //根据题意定义一个结构体放0-n号结点的信息（字母及左右孩子的标号） 

建立树

方法：这个就是老套路了，按照编号（下标）输入数据和孩子编号，更改孩子结点的flag值，最后遍历所有结点来找出根节点

int input(node t[])
{  //输入数据并返回根结点的标号 
    int n;
    char ch1,ch2;
    cin>>n;  //输入一棵树总共结点数 
    if(n==0)
    return -1;  //如果是空树就直接返回 不同构了 
    bool test[n]={false};  //定义一个布尔数组来标记每个结点是否有双亲 
    for(int i=0;i<n;i++)
    {  //从0开始读入对应标号的结点的信息 
        cin>>t[i].data;
        cin>>ch1>>ch2;
        if(ch1!='-')
        {  //如果左孩子不为空就成为对应结点的左孩子 
            t[i].lchild=ch1-'0';
            test[ t[i].lchild ]=true;  //左孩子标号的那个结点就是有双亲的了 
        }
        else 
        t[i].lchild=-1;  //左孩子为空则标记为-1 
        if(ch2!='-')
        {
            t[i].rchild=ch2-'0';
            test[ t[i].rchild ]=true;
        }
        else 
        t[i].rchild=-1;
    }
    for(int j=0;j<n;j++)
    {  //从0开始逐一判断每个结点是否有双亲 
        if(!test[j])  //没有双亲的就是根结点 
        return j;
    }
}

比较判断是否同构

方法：分两种情况来讨论

树空的情况1.两棵树都为空 （同构）  2.一棵树为空另一棵树不为空 （不同构）

树不为空的情况1.结点的数据不相等（不同构）  2.结点数据相等继续比较左左孩子和右右孩子（若都同构则两棵树同构）  3.结点数据相等但左左孩子和右右孩子不同构则继续比较左右和右左孩子（若都同构则两棵树同构）  4.结点数据相等但左左右右，左右右左都不同构则两棵树不同构

int match(int r1,int r2)
{  //判断是否同构 
    if(r1==-1&&r2==-1)
    return 0;//如果两棵树都为空则不同构 
    if((r1==-1&&r2!=-1) || (r1!=-1&&r2==-1))
    return 0;  //两棵树一棵为空，一棵不为空则不同构 
    if(t1[r1].data!=t2[r2].data)
    return 0;  //如果非空但数据不相等则不同构 
    if(match(t1[r1].lchild,t2[r2].lchild) && match(t1[r1].rchild,t2[r2].rchild))
    return 1;  //如果非空且数据相等则继续比较左左 右右 
    if(match(t1[r1].lchild,t2[r2].rchild) && match(t1[r1].rchild,t2[r2].lchild))
    return 1;  //如果非空且数据相等但左左右右不相等则比较左右 右左 
    
    return 0;  //以上包含了空的情况和非空时同构的情况最后加上不同构的时候 
}

最后贴上全部代码

#include <iostream>
using namespace std;

typedef struct
{
    char data;
    int lchild,rchild;
}node;  //根据题意定义一个结构体放0-n号结点的信息（字母及左右孩子的标号） 

node t1[11],t2[11];  //定义两个结构体类型的数组 
 
int input(node t[])
{  //输入数据并返回根结点的标号 
    int n;
    char ch1,ch2;
    cin>>n;  //输入一棵树总共结点数 
    if(n==0)
    return -1;  //如果是空树就直接返回 不同构了 
    bool test[n]={false};  //定义一个布尔数组来标记每个结点是否有双亲 
    for(int i=0;i<n;i++)
    {  //从0开始读入对应标号的结点的信息 
        cin>>t[i].data;
        cin>>ch1>>ch2;
        if(ch1!='-')
        {  //如果左孩子不为空就成为对应结点的左孩子 
            t[i].lchild=ch1-'0';
            test[ t[i].lchild ]=true;  //左孩子标号的那个结点就是有双亲的了 
        }
        else 
        t[i].lchild=-1;  //左孩子为空则标记为-1 
        if(ch2!='-')
        {
            t[i].rchild=ch2-'0';
            test[ t[i].rchild ]=true;
        }
        else 
        t[i].rchild=-1;
    }
    for(int j=0;j<n;j++)
    {  //从0开始逐一判断每个结点是否有双亲 
        if(!test[j])  //没有双亲的就是根结点 
        return j;
    }
}

int match(int r1,int r2)
{  //判断是否同构 
    if(r1==-1&&r2==-1)
    return 0;//如果两棵树都为空则不同构 
    if((r1==-1&&r2!=-1) || (r1!=-1&&r2==-1))
    return 0;  //两棵树一棵为空，一棵不为空则不同构 
    if(t1[r1].data!=t2[r2].data)
    return 0;  //如果非空但数据不相等则不同构 
    if(match(t1[r1].lchild,t2[r2].lchild) && match(t1[r1].rchild,t2[r2].rchild))
    return 1;  //如果非空且数据相等则继续比较左左 右右 
    if(match(t1[r1].lchild,t2[r2].rchild) && match(t1[r1].rchild,t2[r2].lchild))
    return 1;  //如果非空且数据相等但左左右右不相等则比较左右 右左 
    
    return 0;  //以上包含了空的情况和非空时同构的情况最后加上不同构的时候 
}

int main()
{
    int root1,root2;
    root1=input(t1);  //接收数据生成一棵树并返回根结点的标号 
    root2=input(t2);
    if(match(root1,root2)) //调用函数返回判断结果 
       cout<<"Yes";
    else 
       cout<<"No";
       return 0;   
}