模式匹配之KMP的next
关于模式匹配其实只是BF算法的高级版,只是母串不用回溯,模式串回溯而已
int index_kmp(string s,string t,int ssize,int tsize) { //用KMP算法返回匹配时主串的位置否则返回0 int i=0,j=0; while(i<ssize&&j<tsize) { //两个串未到末尾则继续比较 if(j==-1||s[i]==t[j]) //不可以忽略J的判值 { //若相等则继续比较下一个 i++; j++; } else { //若不相等则模式串回溯
i=i-j;
j=1; j=nex[j]; } } if(j==tsize) //若模式串完全比较完则正确并返回在主串的位置 return i-j+1; else return 0; }
最重要的就是NEXT数组的求取,这个我看了好几次书都没看懂,开始是清楚的后来就越看越晕了,上网看了一些算法,发现两种解释
1,利用数学递归求取

假设我们已经知道next[j]的值为K,NEXT[K],黄色区域为next[ 绿色 ]

1.由"next[j] == k;"这个条件,我们可以得到A1子串 == A2子串(根据next数组的定义,前后缀那个)。
2.由"next[k] == 绿色色块所在的索引;"这个条件,我们可以得到B1子串 == B2子串。
3.由"next[绿色色块所在的索引] == 黄色色块所在的索引;"这个条件,我们可以得到C1子串 == C2子串。
4.由1和2(A1 == A2,B1 == B2)可以得到B1 == B2 == B3。
5.由2和3(B1 == B2, C1 == C2)可以得到C1 == C2 == C3。
6.B2 == B3可以得到C3 == C4 == C1 == C2
接下来我们就推导第J+1为的NEXT值及NEXT[J+1] ,就是当第J+1位失配时该回溯的值,next[j+1]即是找strKey从0到j这个子串的最大前后缀:
如果第J个元素的回溯值(next[j]=k) str[k]=str[j],由NEXT的性质(最长相等前后缀)可知next[j+1]=++k; (A1=A2)

如果第J个元素的回溯值(next[j]=k) str[k]!=str[j],就是说我们要回到K前去找最长相等前后缀(这不就是next[k]的值吗)来跟str[j]比较,我们分析str[j] 与str[next[k]] (绿色部分)是否相等,既然是跟上面的分析 (str[k]=str[j])一样都是跟str[j]比较,为何不直接把k换成next[k],继续使用上面的过程(递归调用的道理呀)
由于j+1位之前的next数组我们都是假设已经求出来了的,因此,上面这个递归总会结束,从而得到next[j+1]的值。
我们唯一欠缺的就是初始条件了:
next[1] = 0, (模式串的位置与下表对应的情况,若不是就直接next[0]=-1)如果第一个元素就失配了就不存在回溯了呀
k = 0, 用k来记录回溯的值初始化当然是不用回溯即0(-1)
j = 1, 用j来记录“母串”(其实就是模式串,因为next数组就是模式串自我比较出来的)比较到那里
另外有个特殊情况是k为0时,(前面没有最长相等前后缀不就是需要模式串从第一个与母串的i+1个比较)不能继续递归了,此时next[j+1]应该等于1,即把j回退到首位。
即 next[j+1] = 0; 也可以写成next[++j] = ++k;
void getNext(sstring str,int next[]) { int j = 1; int k = 0; next[1] = 0; // 根据已知的前j位推测第j+1位 while (j < str.length ) { if (k == 0 || str[j] == str[k]) { next[++j] = ++k; } else { k = next[k]; } } return next; }
根据书本上的优化,上面的代码其实有个小问题,这里我们回到真正的母串与模式串对比的情况,我们不是假设j+1位失配(才去算next[j+1]的嘛),如果回溯的值(next[j+1])发现与之前比较的值str[j]一样,这不就是等于没回溯吗,所以就要再回溯一次
void getNext(sstring str,int next[]) { int j = 1; int k = 0; next[1] = 0;// 根据已知的前j位推测第j+1位 while (j < str.length ) { if (k == 0 || str[j] == str[k]) { if(str[k+1]==str[j+1]) { //如果继续失配就继续回退 next[++j]=next[++k]; } else next[++j] = ++k; } else { k = next[k]; } } return next; }
参考了网上的图,其实看完别人的解释自己其实也还不是太懂,但是在写博客时就突然有种恍然大悟地感觉,自己跟着解释一步一步推
2.这也有点像递归(但这个有点……)
void makeNext(string p,int next[]) { int q,k;//q:模版字符串下标;k:最大前后缀长度 int m = P.length();//模版字符串长度 next[1] = 0;//模版字符串的第一个字符的最大前后缀长度为0 for (q = 2,k = 0; q < m; ++q)//for循环,从第二个字符开始,依次计算每一个字符对应的next值 { while(k > 0 && P[q] != P[k])//递归的求出P[0]···P[q]的最大的相同的前后缀长度k k = next[k-1]; //不理解没关系看下面的分析,这个while循环是整段代码的精髓所在,确实不好理解 if (P[q] == P[k])//如果相等,那么最大相同前后缀长度加1 { k++; } next[q] = k; } }
while循环所做的工作:
- 已知前一步计算时最大相同的前后缀长度为k(k>0),即P[0]···P[k-1];
- 此时比较第k项P[k]与P[q],如图1所示
- 如果P[K]等于P[q],那么很简单跳出while循环;
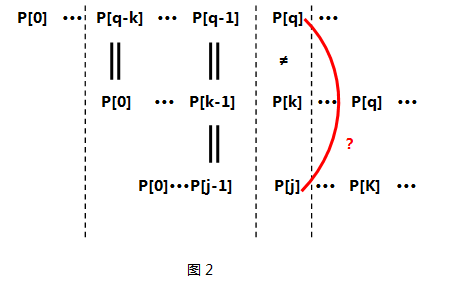
- 关键!关键有木有!关键如果不等呢???那么我们应该利用已经得到的next[0]···next[k-1]来求P[0]···P[k-1]这个子串中最大相同前后缀,可能有同学要问了——为什么要求P[0]···P[k-1]的最大相同前后缀呢???是啊!为什么呢? 原因在于P[k]已经和P[q]失配了,而且P[q-k] ··· P[q-1]又与P[0] ···P[k-1]相同,看来P[0]···P[k-1]这么长的子串是用不了了,那么我要找个同样也是P[0]打头、P[k-1]结尾的子串即P[0]···P[j-1](j==next[k-1]),看看它的下一项P[j]是否能和P[q]匹配。如图2所示

参考了网上的图文,希望这个解释我没有理解吧,如果理解不了next数组的求法就直接把KMP算法复制过来修改增加几个值(毕竟next就是模式串与模式串的模式匹配嘛)
strcat函数:
将两个char类型连接。
char d[20]="GoldenGlobal"; char *s="View"; strcat(d,s);
结果放在d中
printf("%s",d);
输出 d 为 GoldenGlobalView (中间无空格)
d和s所指内存区域不可以重叠且d必须有足够的空间来容纳s的字符串。
返回指向d的指针。
原型是 extern char *strcat(char *dest, const char *src);
把src所指字符串添加到dest结尾处(覆盖dest结尾处的'\0')。
strcpy函数:
原型声明:char *strcpy(char* dest, const char *src);
头文件:#include <string.h> 和 #include <stdio.h>
功能:把从src地址开始且含有NULL结束符的字符串复制到以dest开始的地址空间
说明:src和dest所指内存区域不可以重叠且dest必须有足够的空间来容纳src的字符串。
返回指向dest的指针。





