程序员基本功系列2——排序算法
1、衡量排序算法的标准
其实几乎所有算法都可以从几个方便进行衡量：执行效率、内存开销、稳定性。
排序算法也一样，主要从：
• 时间复杂度，包括：最好情况、最坏情况、平均时间复杂度、还有比较和交换的次数
• 空间复杂度，如：原地排序
• 排序算法的稳定性，即相同数值的元素，排序后的前后顺序不变则称为稳定排序
来汇总一下常用排序算法：
| 算法分类 | 时间复杂度 | 空间复杂度 | 是否基于比较 | 是否稳定排序 |
| 冒泡、插入、选择 | O(n2) | O(1) | 是 | 冒泡和插入是稳定排序，选择是非稳定排序 |
| 快排、归并 | O(nlogn) | 快排O(1)，归并O(n) | 是 | 归并是稳定排序，快速是非稳定排序 |
| 桶排序、计数、基数 | O(n) | 都不是原地排序 | 否 | 是 |
2、冒泡、插入和选择
2.1、冒泡排序
举个简单的例子：对数组[4,5,6,3,2,1]进行排序。看下冒泡过程分解：
算法思路：总是将左侧未排序数组中最大的元素依次有序放到右侧排序数组中。循环n次，每次从0开始，到n-1-i结束，相邻数组两两比较，每次将大的元素交换到后面，从而一点点冒泡到右侧有序数组中。
冒泡排序包含两个关键操作：比较和交换，根据上面的分析，我们写出具体的代码：
// 冒泡排序，a表示数组，n表示数组大小 public void bubbleSort(int[] a, int n) { if (n <= 1) return; for (int i = 0; i < n; ++i) { // 提前退出冒泡循环的标志位 boolean flag = false; for (int j = 0; j < n - i - 1; ++j) { if (a[j] > a[j+1]) { // 交换 int tmp = a[j]; a[j] = a[j+1]; a[j+1] = tmp; flag = true; // 表示有数据交换 } } if (!flag) break; // 没有数据交换，提前退出 } }
冒泡排序比较简单，注意这里我们设置了一个退出标志位，当数组已经当前位置后续元素已经有序的情况下，减少不必要的循环逻辑。
性能分析：
• 冒泡排序的最好情况下时间复杂度，即数组有序时（1，2，3，4，5，6），是O(n)；最坏情况时间复杂度，即数组逆序（6，5，4，3，2，1），是O(n2)；平均时间复杂度是 O(n2)。
• 冒泡排序是原地排序，空间复杂度 O(1)。
• 冒泡排序是稳定是排序，因为 a[j] == a[j+1] 时没有进行交换，所以前后顺序不会变。
2.2、插入排序
插入排序思想：将数组中的数据分为两个区间，已排序区间和未排序区间。初始已排序区间只有一个元素，就是数组的第一个元素。然后取未排序区间中的元素，在已排序区间中找到合适的插入位置将其插入，并保证已排序区间数据一直有序。重复这个过程，直到未排序区间中元素为空，算法结束。
对数组[4,5,6,3,2,1]进行排序，看下插入过程分解：
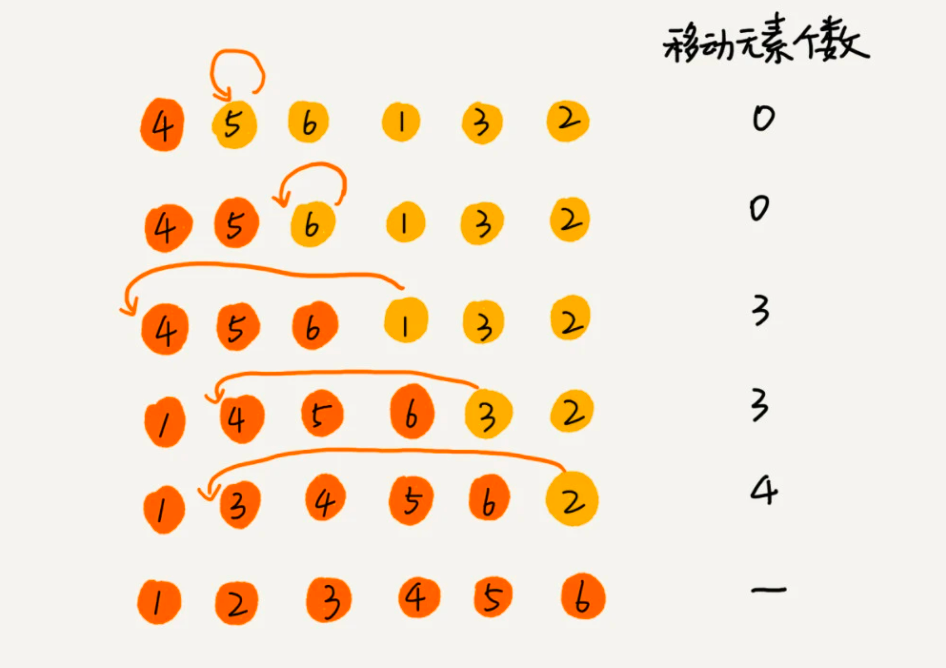
根据以上分析，我们写出具体代码：
// 插入排序，a表示数组，n表示数组大小 public void insertionSort(int[] a, int n) { if (n <= 1) return; for (int i = 1; i < n; ++i) { int value = a[i];// 查找插入的位置
int j=i-1; for (; j >= 0; --j) { if (a[j] > value) { a[j+1] = a[j]; // 数据移动 } else { break; } } a[j+1] = value; // 插入数据，注意这里是a[j+1]，因为循环结束找到要插入位置后，后面的--j还会执行。 } }
性能分析：
• 插入排序的最好情况下时间复杂度，即数组有序时（1，2，3，4，5，6），是O(n)；最坏情况时间复杂度，即数组逆序（6，5，4，3，2，1），是O(n2)；平均时间复杂度是 O(n2)。
• 插入排序是原地排序，空间复杂度 O(1)。
• 插入排序是稳定是排序，因为 a[j] == value 时没有将 a[j] 移动，所以前后顺序不会变。
2.3、选择排序
选择排序算法的实现思路有点类似插入排序，也分已排序区间和未排序区间。但是选择排序每次会从未排序区间中找到最小的元素，将其放到已排序区间的末尾。
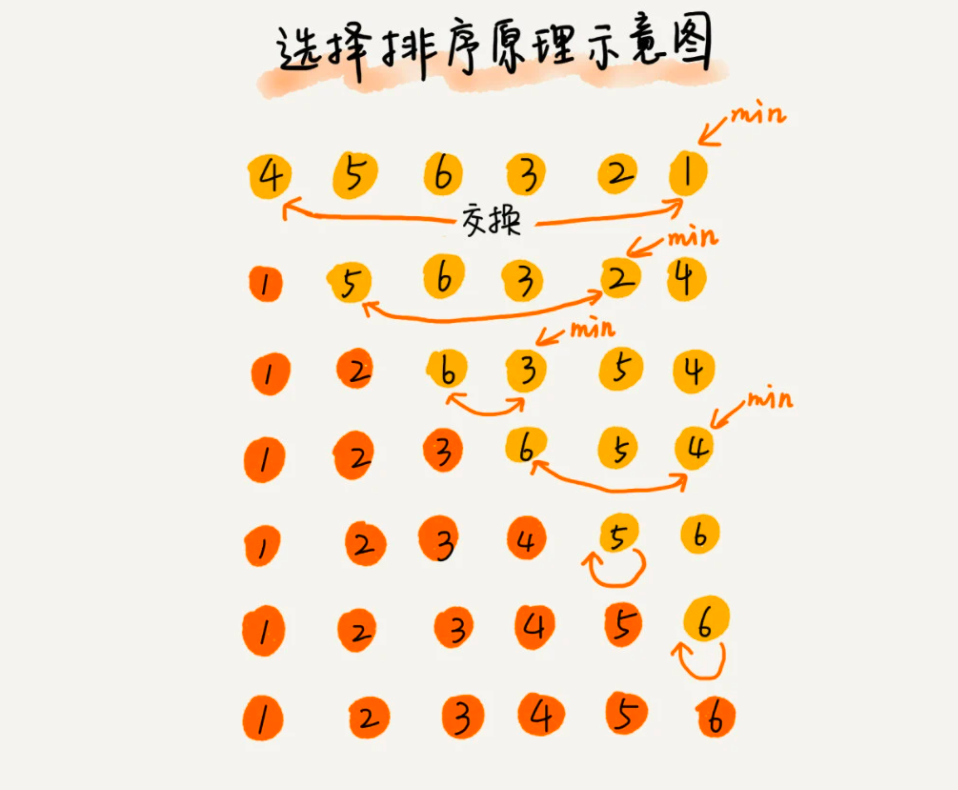
根据以上分析，我们写出代码：
// 选择排序，a表示数组，n表示数组大小 public void selectSort(int[] a, int n) { if (n <= 1) return; for (int i = 0; i < n; ++i) { int min_idx = i; // 找到最小元素的位置 for (int j=i+1; j < n; ++j) { if (a[j] < a[min_idx]) { min_idx = j; } } //移动未排序区最小元素到排序区 if(min_idx != i){ int tmp = a[i]; a[i] = a[min_idx]; a[min_idx] = tmp; } } }
性能分析：
• 选择排序的最好情况下时间复杂度，即数组有序时（1，2，3，4，5，6），是O(n)；最坏情况时间复杂度，即数组逆序（6，5，4，3，2，1），是O(n2)；平均时间复杂度是 O(n2)。
• 选择排序是原地排序，空间复杂度 O(1)。
• 选择排序是不稳定是排序，因为每次都要找到未排序区最小元素和前面的元素交换位置，这样破坏了稳定性。例如：[5,8,5,2,4]，当第一个5和2交换位置时稳定性就被破坏了。
3、快速和归并
快速排序和归并排序都用到了分治思想，适合大规模数据排序，比上面三种更常用。
3.1、归并排序
归并排序的核心思想是：把数组从中间分成前后两部分，然后对前后两部分分别排序，再将排好序的两部分合并在一起，这样整个数组就都有序了。
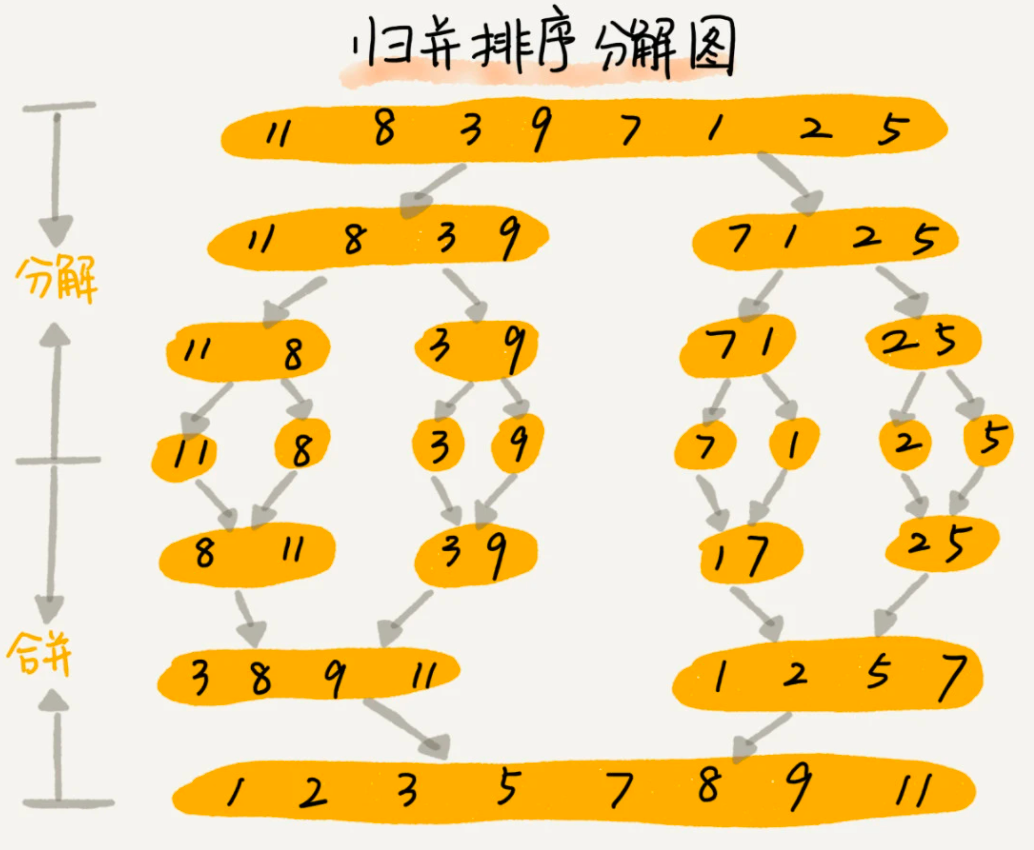
分治思想都会用到递归，我们来看下递推公式：
merge_sort(p..r) = merge_sort(p...m) + merge_sort(m+1...r)，终止条件：当 p >= r 时不再继续分解。
到这里，分解的过程就结束了，但是分解后还有一个合并的过程，就是将已经有序的 A[p...m] 和 A[m+1...r] 合并成一个有序数组，然后放入 A[p...r]。
合并的逻辑：申请一个临时数组 tmp，大小与 A[p...r] 相同。用两个游标 i 和 j，分别指向 A[p...m]和 A[m+1...r]的第一个元素。比较这两个元素 A[i] 和 A[j]，如果 A[i]<=A[j]，就把 A[i] 放入到临时数组 tmp，并且 i 后移一位，否则将 A[j]放入到数组 tmp，j 后移一位。继续上述比较过程，直到其中一个子数组中的所有数据都放入临时数组中，再把另一个数组中的数据依次加入到临时数组的末尾，这个时候，临时数组中存储的就是两个子数组合并之后的结果了。最后再把临时数组 tmp 中的数据拷贝到原数组 A[p...r]中。
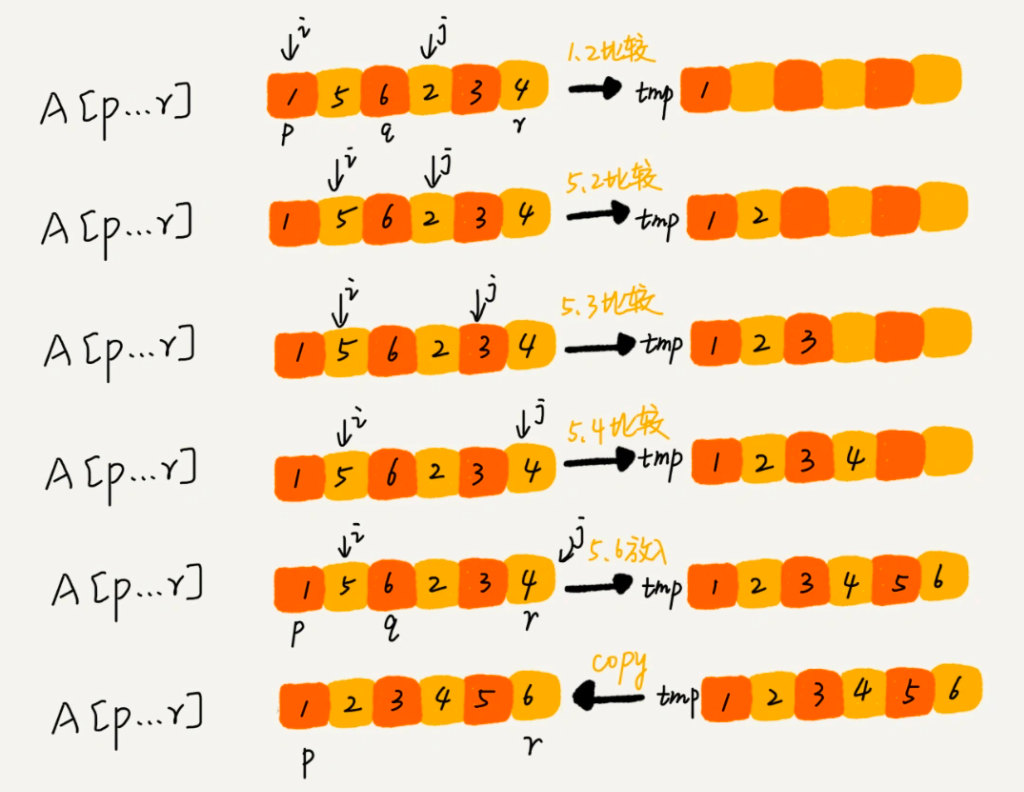
根据以上分析，我们写出整个分解与合并的代码：
public class MergeSort { public static void main(String[] args) { int[] arr = {4,5,6,3,2,1}; int len = arr.length; sort(arr,0,len-1); for (int item : arr){ System.out.print(item); } } /** * 分解 */ private static void sort(int[] arr,int left,int right){ //终止条件 if (left >= right)return; int mid = (left+right) / 2; sort(arr,left,mid); sort(arr,mid+1,right); //如果两个数组已经有序，就不用再合并了 if (arr[mid] <= arr[mid+1]){ return; } //合并两段区间 merge(arr,left,mid,right); } /** * 合并 */ private static void merge(int[] arr,int left,int mid,int right){ //创建临时数组 int[] tmp = new int[right-left+1]; int i=left,j=mid+1; for (int k=0;k<tmp.length;k++){ //如果左侧 if (i == mid+1){ tmp[k] = arr[j++]; }else if (j == right+1){ tmp[k] = arr[i++]; } //这一步如果去掉等号，就破坏调了稳定性 else if (arr[i] <= arr[j]){ tmp[k] = arr[i++]; }else { tmp[k] = arr[j++]; } } //采用Java自带的数组拷贝，也可以写个循环 System.arraycopy(tmp, 0,arr, left, tmp.length); } }
性能分析：
• 归并排序的时间复杂度在最坏、最好、平均情况下都是 O(nlogn)，所以时间复杂度非常稳定。
时间复杂度分析：因为每次都需要把当前数组分成两部分，所以对于长度为n的数组，需要拆分成logn层，每层合并时都要遍历所有元素，时间复杂度就是O(n)，因为总的时间复杂度就是O(nlogn)。但是在merge函数执行前加了if(nums[mid] < nums[mid+1]) return 判断，所以当原数组越有序时，合并次数越少，因此归并排序的时间复杂度<=O(nlogn)。
• 归并排序并不是原地排序，合并时需要申请额外空间，的空间复杂度是 O(n)，这也是其不如快排使用广泛的原因。
• 归并排序是稳定排序，关键在于合并过程 arr[i] <= arr[j] 的判断，相等元素将左侧的元素先放入临时数组 tmp 中。
3.2、快速排序
快排也是采用的分治思想，核心逻辑：如果要排序数组中下标从 p 到 r 之间的一组数据，选择 p 到 r 之间的任意一个数据作为 pivot（分区点）。遍历 p 到 r 之间的数据，将小于 pivot 的放到左边，将大于 pivot 的放到右边，将 pivot 放到中间。经过这一步骤之后，数组 p 到 r 之间的数据就被分成了三个部分，前面 p 到 q-1 之间都是小于 pivot 的，中间是 pivot，后面的 q+1 到 r 之间是大于 pivot 的。
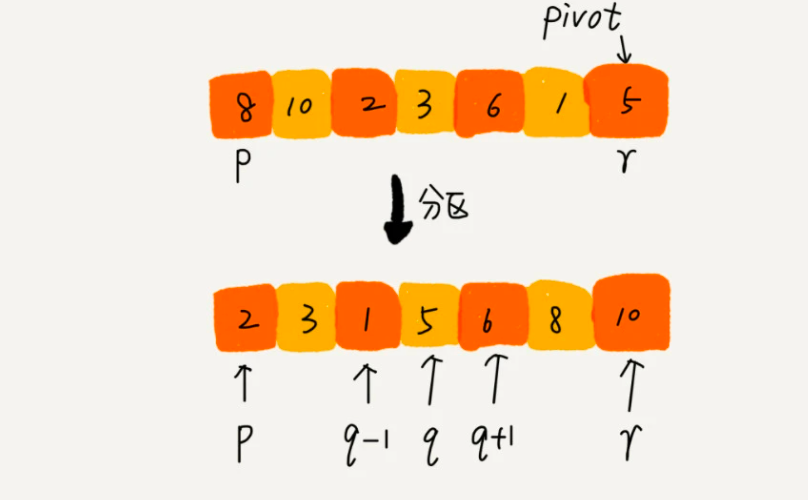
根据上面的分析，快排可以将 p-r 之前的排序分解为 p-q 和 q+1-r 两个子问题。然后逐步分解，知道区间为 1 时全部有序结束。我们写出递推公式：
quick_sort(p...r) == quick_sort(p...q) + quick_sort(q+1...r)，终止条件：当 p >= r 时结束不再分解。
我们写一段伪代码来表示上面分析的过程：
// 快速排序，A是数组，n表示数组的大小 quick_sort(A, n) { quick_sort_c(A, 0, n-1) } // 快速排序递归函数，p,r为下标 quick_sort_c(A, p, r) { if p >= r then return q = partition(A, p, r) // 获取分区点 quick_sort_c(A, p, q-1) quick_sort_c(A, q+1, r) }
快排虽然没有归并排序的 merge() 函数，但是会在分解前有一个分区的过程 partition()。所以要先分析分区过程：
就是随机选择一个元素作为 pivot（一般情况下，可以选择 p 到 r 区间的最后一个元素），然后对 A[p...r]分区，函数返回 pivot 的下标。可以粗暴的申请两个数组，将小于分区点的放入一个，大于的放入另一个然后再合并。但是为了降低空间复杂度，我们选择双指针元素交换的方式实现原地排序。具体做法就是两个指针 i 和 j，i 指向大于分区点的位置，j 表示当前位置，如果当前位置小于分区点，则交换 i 和 j ，这样最后 i 的位置就是分区点，再将 i 和 povit 交换。图解：
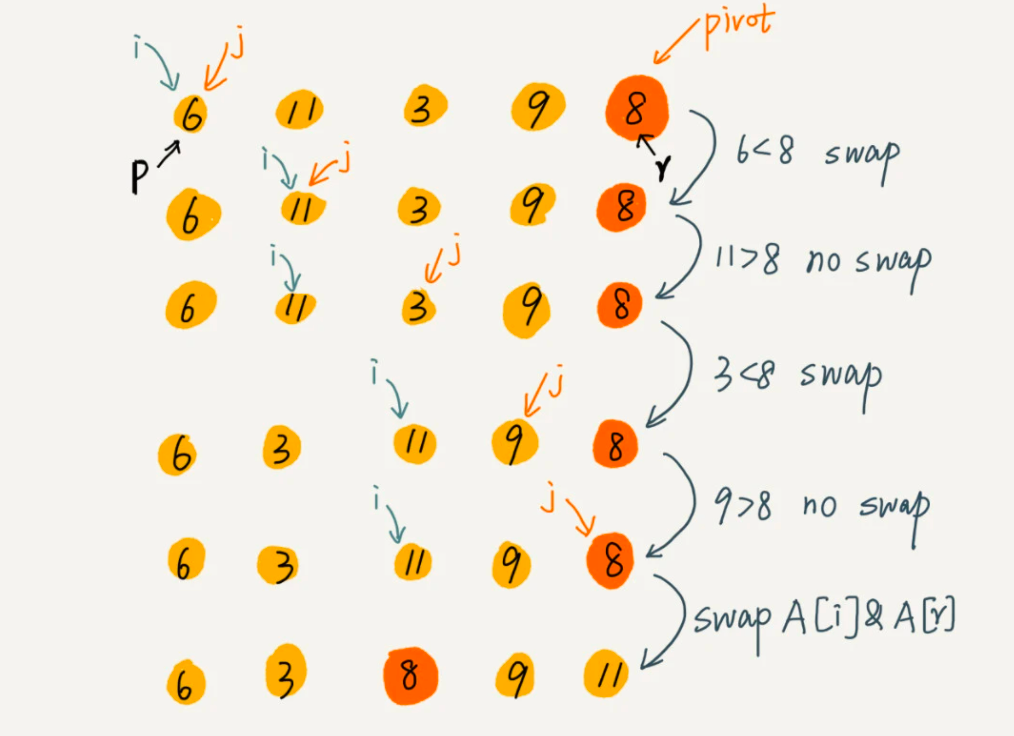
这个分解我们就不写伪代码了，经过上面的分析，我们直接写出整个分区和分解排序的过程代码：
public class QuickSort { public static void main(String[] args) { int[] arr = {4,5,6,3,2,1}; sort(arr,0,arr.length-1); for (int item : arr){ System.out.print(item); } } /** * 分解 */ private static void sort(int[] arr,int left,int right){ //终止条件 if (left >= right)return; //获取分区位置 int povit = partition(arr,left,right); //分解 sort(arr,left,povit-1); sort(arr,povit+1,right); } /** * 通过双指针、原地交换的方式实现原地排序 */ private static int partition(int[] arr,int left,int right){ //i指针指向比基准点大的位置 int i=left; //选取最后一个元素为基准点 int povit = arr[right]; for (int j=left;j<right;j++){ //如果当前位置小于基准点，则和大于基准点的位置交换 if (arr[j] < povit){ swap(arr,i,j); i++; } } //最后将基准点换到分区位置 swap(arr,i,right); return i; } private static void swap(int[] arr,int i,int j){ int tmp = arr[i]; arr[i] = arr[j]; arr[j] = tmp; } }
性能分析：
• 快速排序是原地排序，空间复杂度 O(1)
• 快速排序是不稳定的排序
• 快速排序的最好和平均时间复杂度是 O(nlogn)，但是当数组是有序的情况下，如[1,2,3,4,5,6]，因为每次都选取最后一个元素为分区点，所以时间复杂度会退化成 O(n2)
时间复杂度分析：也是拆分分析，分区函数partition要遍历当前数组的所有元素，的时间复杂度是O(n)，理想情况下，每次一次分区都能将原数组分成两部分，这样层数也像归并排序一样达到logn层，那时间复杂度就是O(n)*O(logn)=O(nlogn)；但如果每次选取的基准点都是极端元素（最大或最小），那每一层相当于只能排序基准点一个元素，层数也会变成n层，时间复杂度就是O(n)*O(n)=O(n2)。
接下来我们来分析一下归并和快速两种算法的区别：
二者都是分治思想，先来看张图看下二者的区别
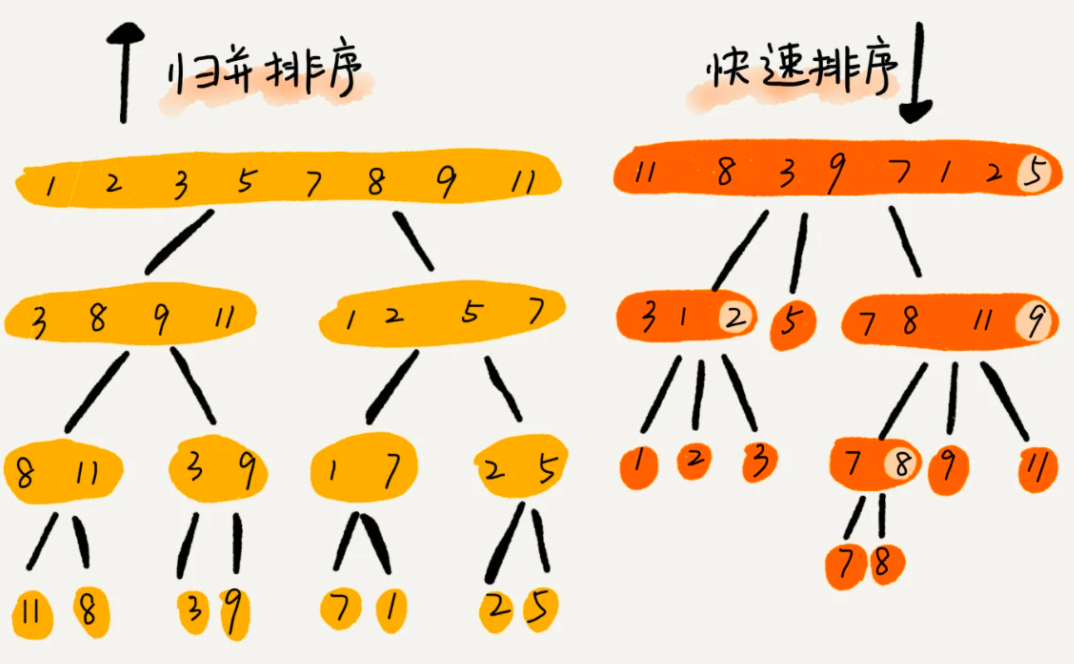
可以发现，归并排序的处理过程是由下到上的，先处理子问题，然后再合并。而快排正好相反，它的处理过程是由上到下的，先分区，然后再处理子问题。归并排序虽然是稳定的、时间复杂度为 O(nlogn) 的排序算法，但是它是非原地排序算法，主要原因是合并函数无法在原地执行。快速排序通过设计巧妙的原地分区函数，可以实现原地排序，解决了归并排序占用太多内存的问题。
案例：
leetcode 215. 数组中的第K个最大元素，可以利用快速排序的分区方式来求解，时间复杂度 O(n)。
4、线性排序——桶排序、计数排序、基数排序
因为这三种排序算法的时间复杂度都是 O(n)，是线性的，所以也叫线性排序。并且他们都不是基于比较的。
另外这三种算法理解不难，但是对于要排序数据的要求比较苛刻，所以还要重点分析这三种排序的适用场景。
4.1、桶排序
核心思想：将要排序的数据分到几个有序的桶里，每个桶里的数据再单独进行排序。桶内排完序之后，再把每个桶里的数据按照顺序依次取出，组成的序列就是有序的了。
时间复杂度分析：
如果要排序的数据有 n 个，把它们均匀地划分到 m 个桶内，每个桶里就有 k=n/m 个元素。每个桶内部使用快速排序，时间复杂度为 O(k * logk)。m 个桶排序的时间复杂度就是 O(m * k * logk)，因为 k=n/m，所以整个桶排序的时间复杂度就是 O(n*log(n/m))。当桶的个数 m 接近数据个数 n 时，log(n/m) 就是一个非常小的常量，这个时候桶排序的时间复杂度接近 O(n)。
对数据要求比较苛刻：
• 要排序的数据需要很容易就能划分成 m 个桶，并且，桶与桶之间有着天然的大小顺序。这样每个桶内的数据都排序完之后，桶与桶之间的数据不需要再进行排序。
• 数据在各个桶之间的分布是比较均匀的。如果数据经过桶的划分之后，有些桶里的数据非常多，有些非常少，很不平均，那桶内数据排序的时间复杂度就不是常量级了。在极端情况下，如果数据都被划分到一个桶里，那就退化为 O(nlogn) 的排序算法了。
桶排序适用的场景：
桶排序比较适合用在外部排序中。所谓的外部排序就是数据存储在外部磁盘中，数据量比较大，内存有限，无法将数据全部加载到内存中。我们来分析下这种场景利用桶排序的解决思路：
可以先扫描一遍文件，看订单金额所处的数据范围。假设经过扫描之后得到，订单金额最小是 1 元，最大是 10 万元。将所有订单根据金额划分到 100 个桶里，第一个桶我们存储金额在 1 元到 1000 元之内的订单，第二桶存储金额在 1001 元到 2000 元之内的订单，以此类推。每一个桶对应一个文件，并且按照金额范围的大小顺序编号命名（00，01，02...99）。理想的情况下，如果订单金额在 1 到 10 万之间均匀分布，那订单会被均匀划分到 100 个文件中，每个小文件中存储大约 100MB 的订单数据，我们就可以将这 100 个小文件依次放到内存中，用快排来排序。等所有文件都排好序之后，只需要按照文件编号，从小到大依次读取每个小文件中的订单数据，并将其写入到一个文件中，那这个文件中存储的就是按照金额从小到大排序的订单数据了。不过，你可能也发现了，订单按照金额在 1 元到 10 万元之间并不一定是均匀分布的 ，所以 10GB 订单数据是无法均匀地被划分到 100 个文件中的。有可能某个金额区间的数据特别多，划分之后对应的文件就会很大，没法一次性读入内存。这又该怎么办呢？针对这些划分之后还是比较大的文件，我们可以继续划分，比如，订单金额在 1 元到 1000 元之间的比较多，我们就将这个区间继续划分为 10 个小区间，1 元到 100 元，101 元到 200 元，201 元到 300 元....901 元到 1000 元。如果划分之后，101 元到 200 元之间的订单还是太多，无法一次性读入内存，那就继续再划分，直到所有的文件都能读入内存为止。
4.2、计数排序
计数排序可以看作桶排序的一种特殊情况，适用于数据范围不大的场景。例如，数据范围0-k，就将数据分为k个桶，每个桶的数值相等。
案例：假设有50万考生，满分是900分，最低0分，要根据分数查询考生的具体排名。
可以分成 901 个桶，对应分数从 0 分到 900 分。根据考生的成绩，将这 50 万考生划分到这 901 个桶里。桶内的数据都是分数相同的考生，所以并不需要再进行排序。只需要依次扫描每个桶，将桶内的考生依次输出到一个数组中，就实现了 50 万考生的排序。因为只涉及扫描遍历操作，所以时间复杂度是 O(n)。
计数体现在什么地方呢？就是再申请一个大小为901的数组，分别记录每个桶元素的个数，这样就可以根据分数确定考生的排名了。
4.3、基数排序
基数排序对要排序的数据是有要求的，需要可以分割出独立的“位”来比较，而且位之间有递进的关系，如果 a 数据的高位比 b 数据大，那剩下的低位就不用比较了。除此之外，每一位的数据范围不能太大，要可以用线性排序算法来排序，否则，基数排序的时间复杂度就无法做到 O(n) 了。
例如：有10万个手机号，对这10万个手机号进行排序。先按照最后一位使用稳定的排序算法来排序手机号码（注意一定要使用稳定的排序算法），然后，再按照倒数第二位重新排序，以此类推，最后按照第一位重新排序。经过 11 次排序之后，手机号码就都有序了。
5、堆排序
这块只看一下代码，堆的具体分析程序员基本功系列6——堆
public class HeapSort { public static void main(String[] args) { int[] num = {100,7,40,30,83,4,15,1}; sort(num); for (int item : num) { System.out.println(item); } } private static void sort(int[] arr){ //1、建堆 buildHeap(arr); //2、排序 int k = arr.length-1; while (k > 0){ //将堆顶元素（最大）与最后一个元素交换位置 swap(arr,k, 0); //将剩下的元素重新堆化 heapify(arr,--k,0); } } /** * 建堆 */ private static void buildHeap(int[] arr){ //对于完全二叉树，(arr.length-1) / 2是最后一个叶子节点的父节点，叶子节点不用堆化 for(int i=(arr.length-1)/2;i >= 0;i--){ heapify(arr,arr.length-1,i); } } /** * 堆化， */ private static void heapify(int[] arr,int n,int i){ //当前节点小标i，那它的左子节点就是i*2，右子节点就是i*2+1 while (true){ int maxPos = i; //与左子节点比较，获取最大值位置 if (i*2 <= n && arr[i] < arr[i*2]){ maxPos = i*2; } //与右子节点比较，获取最大值位置 if (i*2+1 <= n && arr[maxPos] < arr[i*2+1]){ maxPos = i*2+1; } //最大值是当前位置，结束循环 if (maxPos == i){ break; } //与子节点交换位置 swap(arr,i,maxPos); //以交换后子节点位置继续往下寻找 i = maxPos; } } private static void swap(int[] arr,int a,int b){ int tmp = arr[a]; arr[a] = arr[b]; arr[b] = tmp; } }
