次小生成树
次小生成树，就是求除了最小生成树之外最小的那个生成树。
下面介绍一下利用prim求次小生成树的主要步骤。
1.先求出来最小生成树。并将最小生成树任意两点之间路径当中的权值最大的那一条找出来，为什么要找最大的呢，因为生成树加入一条边之后一定构成了回路，那么肯定要去掉这个回路当中一条边才是生成树，那么，怎么去边才是次小的，那就去掉除了刚刚添加的一条边之外回路当中权值最大的一个，所以留下的就是最小的。
2.枚举最小生成树外的每一条边。找出最小的就是次小生成树。
step 1. 先用prim求出最小生成树T.
在prim的同时，用一个矩阵max[u][v] 记录 在T中连结任意两点u,v的唯一的
路中权值最大的那条边的权值. (注意这里).
这是很容易做到的，因为prim是每次增加一个结点s, 而设已经标号了的结点
集合为W, 则W中所有的结点到s的路中的最大权值的边就是当前加入的这条边.
step 1 用时 O(V^2).
step 2. 枚举所有不在T中的边uv, 加入边uv则必然替换权为max[u][v]的边.
算法实现上,首先用求最小生成树的算法求出其权值之和为mst,然后枚举不属于最小生成树的边(x, y),并添加到最小生成树中,那么树必定形成环,然后删掉这个环内(不包含(x,y))最长的边.然后计算权值之和,枚举所有不属于最小生成树的边,取其权值的最小值,就是次小生成树.
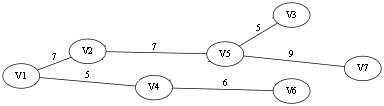
假设上图是图的最小生成树,并存在边(v5, v6),且其权值为8,那么当枚举到此条边时,在图中添加边(v5,v6),图中便有了一个环,在此环中找到除新加边以外最大的边的权值为7,那么删除此边,计算权值,然后继续枚举其他不存在于最小生成树的边,从中取得最小值,就是要求的答案.
