http://blog.csdn.net/v1_vivian/article/details/52038037
牛顿方法也是对解空间进行搜索。
基本思想：对于函数f(x)，如果我们要找到使得函数值为0的x值时，做法如下：
1、随机选一个点（θ0），然后求出该点的切线，即导数。
2、延长它使之与x轴相交，以相交时的x的值（θ1）。
3、重复1、2直到f(x)==0
我们可以得知：其中θ的更新规则为：
对于机器学习问题，我们优化的目标函数为极大似然估计函数，当极大似然估计函数取得最大时，其导数为0。
所以，我们可以使得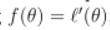
，由此可得：
上面是当参数θ为实数时的情况，当参数为向量时，更新规则为：（其中，H是一个n*n的矩阵，n为参数向量的长度，即特征数，H是函数的二阶导数矩阵，被称为Hessian矩阵，此时，用一个表示一阶导数的向量乘上一个表示二阶导数的矩阵的逆，来表达上式中的一阶导数除以二阶导数）
H矩阵中元素Hij计算公式如下：
牛顿方法的优点：
牛顿方法与梯度下降方法功能一样，都是在寻到解空间，但相比较而言，牛顿方法的优点是收敛速度快，通常只要经过十几次迭代就可以达到收敛。牛顿方法也被称为二次收敛，因为当迭代到距离收敛值比较近的时候，每次迭代都能使误差变为原来的平方。
牛顿方法的缺点：
牛顿方法的缺点是当参数向量较大时，每次迭代都需要计算一次Hessian矩阵的逆，比较耗时。
