poj-1031-fence（不是我写的，我只是想看着方便）

题目大意：

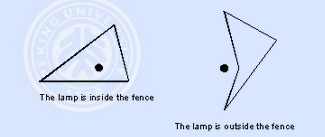
　　有一个光源位于（0,0）处，一个多边形的围墙。围墙是“全黑”的，不透光也不反射光。距光源r处的光强度为I₀=k/r，k为常数。

　　一块无穷窄高为h的墙上围墙受到的照度为dI=I₀*|cosα|*dl*h，其中I₀为该点光强，α为法线与该点到光源连线的夹角。

求总照度。（dI之和）

输入：第一行三个数，第一个数为给定的常数k，第二个数位围墙高h，第三个数为围墙顶点数。接下来每行为一个围墙的顶点，按遍历多边形的顺序给出。

输出：总的照度。

---

Sample Input

0.5 1.7 3
1.0 3.0
2.0 -1.0
-4.0 -1.0

Sample Output

5.34

---

如果有一点点计算机视觉的基础或者物理直觉好的话，会知道结果实际与距离和夹角都没有关系，只要求光源向360°辐射的范围内，有多大的角度被墙挡住了。于是转化为了求围墙相对于光源张角的问题。

求张角的过程大致如下：

遍历所有的边，求边相对于光源的张角（自行规定一个正方向）。记录下每次求和之后的最大值和最小值（即像一个方向延扫得最远时的角度），但要注意不应该大于360度。

#include<iomanip>
#include<iostream>
#include<cmath>
using namespace std;
const  double pi=3.1415926;
double k,h,x[105],y[105];

double angle(double x0,double y0,double x,double y)
{
    double a=atan2(y0,x0);//atan2(X2-X1,Y2-Y1)所表达的意思是坐标原点为起点，
                           指向(x,y)的射线在坐标平面上与x轴正方向之间的角的角度。
    double b=atan2(y,x);//我试过x，y顺序可以翻过来
    if(a-b>pi)b+=pi*2;
    if(b-a>pi)a+=pi*2;
    return a-b;


}
int main()
{int n;
cin>>k>>h>>n;
for(int i=0;i<n;i++)
    cin>>x[i]>>y[i];
x[n]=x[0],y[n]=y[0];
double s=0,max=0,min=0;
for(int i=0;i<n;i++)
{
  s+=angle(x[i],y[i],x[i+1],y[i+1]);//0组与1组，1组与2组，2组在与0组分别求夹角；
 　　　　　　　　　　　　　　　　　　　　　　夹角和为光源照到的区域；

    if(s<min)min=s;
    if(s>max)max=s;
    if(max-min>=2*pi)
    {max=min+2*pi;
    break;}
}

    cout<<fixed<<setprecision(2)<<h*k*(max-min)<<endl;


    return 0;
}