概率图模型导论

引言

　　机器学习中的许多常见问题是彼此独立数据点的分类。例如，给定图像，预测它是包含猫还是狗，或者给出手写字符的图像，预测它是0到9中的哪个数字。然而，事实证明，许多问题不适合上述框架。例如，给定一个句子“我喜欢机器学习”，用它的词性（名词，代词，动词，形容词等）标记每个单词，这个任务无法通过独立处理每个单词来解决 ，由于“学习”可以是名词或动词。对于更复杂的文本处理，例如从一种语言翻译成另一种语言，文本翻译等，这项任务更重要。

　　如何使用标准分类模型来处理这些问题是一个挑战。一个用于此类问题的强大框架是概率图形模型（probabilistic graphical models ，PGM）。在本文中，我将介绍该框架的一些基本内容。

　　在讨论如何将概率图模型应用于机器学习问题之前，我们需要了解PGM框架。 概率图模型（或简称图模型）由图形结构组成， 图的每个节点与随机变量相关联，并且图中的边用于解释随机变量之间的关系。

　　根据图形是有向还是无向，我们可以将图形模式分为两类 ：

• 贝叶斯网络
• 马尔可夫网络

贝叶斯网络：定向图形模型

　　贝叶斯网络的典型例子是所谓的“学生网络”，它看起来像这样：

此图表描述了在大学课程中注册的学生的设置。 图中有5个随机变量：

Difficulty （课程的难度）: 取值0（低难度）和1（高难度）

Intelligence（智力水平）: 取值0（低）和1（高）

Grade（学生的上课成绩） : 取值1（好成绩），2（平均成绩）和3（成绩差）

SAT （SAT考试成绩）: 取0（低分）和1（高分）

Letter（完成课程后学生从教授那里得到推荐信的质量） : 取0（不是好信）和1（好信）

　　图中的边包含变量的依赖关系。学生的“成绩”取决于课程的“难度”和学生的“智力”。反过来，“成绩”决定了学生是否从教授那里得到了一封好的推荐信。此外，除了影响“成绩”之外，学生的“智力”还影响他们的“SAT”分数。值得注意的是，箭头的方向告诉我们因果关系 ：“智力”影响“SAT”分数，但“SAT”分数不影响“智力”。

　　最后，我们可以看到每个节点关联的表，这些被称为条件概率分布（conditional probability distributions ，CPD）。

条件概率分布（CPD）

　　“Difficulty”和“Intelligence”的CPD相当简单，因为这些变量不依赖于任何其他变量。 这些表给出了变量的概率，取值0或1。 可以注意到，每个表中的值必须总和为1。

　　对于“SAT”的CPD，每行对应于其父节点（“ Intelligence”）可能的取值，每列对应于“SAT”可以采用的值。 每个单元格具有条件概率$p（SAT = s | Intelligence = i）$，也就是说，假设“Intelligence”的值是$i$，“SAT”的值是$s$的概率是多少。例如，我们可以看到$p（SAT =s^1| Intelligence =i^1）$是0.8，也就是说，如果学生的智力很高，那么SAT得分高的概率也是0.8。 另一方面，$p（SAT =s^0| Intelligence =i^1）$，如果学生的智力高，则SAT得分低的概率为0.2。

　　每行中值的总和为1.这是有道理的，因为鉴于Intelligence =i¹，SAT分数可以是s⁰或s¹，因此两个概率必须加起来为1.同样，“Letter”的CPD 条件概率$p（Letter = l | Grade = g）$。 因为“等级”可以取三个值，所以我们在此表中有三行。
　　根据上述知识，“Grade”的CPD易于理解。 因为它有两个父节点，条件概率将是p的形式$p(Grade=g | Difficulty=d, SAT=s)$，也就是说，在“Difficulty”的值为 “g'和”SAT“的值为“s”的条件下，“Grade”为g的概率是多少。 

　　贝叶斯网络的基本要求是图必须是有向无环图（directed acyclic graph，DAG）。

马尔可夫网络：无向图形模型

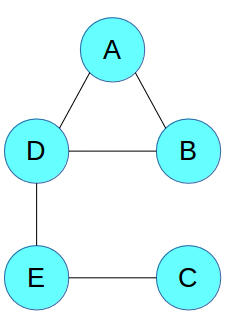
　　为了简洁起见，我们直接看抽象图，边表示变量之间的相互作用。 我们看到，虽然A和B直接相互影响，但A和C没有。

潜在的函数
　　就像我们有贝叶斯网络的CPD一样，我们也用表格来整合马尔可夫网络中节点之间的关系。 但是，这些表格和CPD之间存在两个重要差异。

　　首先，这些值不需要总和为1，也就是说，表并没有定义概率分布，它只告诉我们具有某些值的可能。 其次，没有条件。 它与相关的变量的联合分布成比例，而不是CPD中的条件分布。

　　结果表称为“因子”或“潜在函数”，并使用希腊符号φ表示。 例如，我们可以使用以下函数来捕获三个变量A，B和C之间的关系，如果A和B是不同的，则C可能为1 ，如果A和B相同，则C可能为0：

 

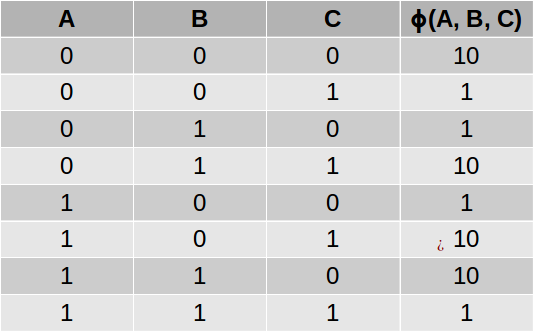
　　通常，我们为图中的每个最大团定义一个潜在的函数。

　　图形结构和表格表达了随机变量上的联合概率分布。

　　我们可能遇到的一个问题是，为什么我们需要有向图和无向图？原因在于，对于某些问题，将它们表示为有向图更为自然，例如上面的学生网络，其中很容易描述变量之间的因果关系 ：学生的智力影响SAT分数，但是SAT分数不会影响学生的智力。

　　对于其他类型的问题，比如图像，我们希望将每个像素表示为一个节点，并且我们知道相邻像素相互影响，但像素之间没有因果关系;相反，它们可能是对称的。因此，在这种情况下，我们使用无向图形模型。

问题
　　到目前为止，我们一直在讨论图形和随机变量和表格，你可能会想到这一切的重点是什么？我们究竟想做什么？机器学习在哪里 - 数据，培训，预测等？本节将解决这些问题。

　　让我们回到学生网络。假设我们有图形结构，我们可以根据我们对世界的了解创建图形结构（在机器学习中称为“领域知识”）。但我们没有CPD表，只有它们的大小。我们确实有一些数据 ：对于大学里的十个不同的班级，我们可以衡量他们的难度。

　　此外，我们有关于每个课程中每个学生的数据 - 他们的智力，他们的SAT成绩是什么，他们得到什么成绩，以及他们是否收到了教授的好信。根据这些数据，我们可以估算CPD的参数。例如，数据可能表明智力较高的学生通常会获得良好的SAT成绩，我们也许可以从中学习$p（SAT = s^1 | Intelligence = i^1）$很高。这是学习阶段。我们很快就会看到我们如何在贝叶斯网络和马尔可夫网络中进行这种参数估计。

　　现在，对于新数据点，您将观察到一些变量，这些变量并不是完整的。例如，在下图中，你将了解课程的难度和学生的SAT分数，并且您想要估计学生获得好成绩的概率。

　　

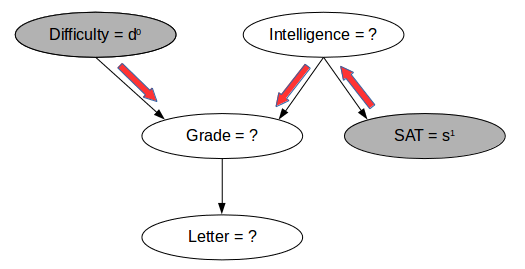
　　虽然我们没有直接向我们提供该信息的CPD，但我们可以看到学生的高SAT分数表明该学生可能是聪明的，因此，如果难度较高，则成绩良好的概率很高。该过程很低，如上图中的红色箭头所示。我们可能还想同时估计多个变量的概率，比如学生获得好成绩的概率和好的信件是什么？

　　具有已知值的变量称为“观察变量”，而未观察到值的变量称为“隐藏变量”或“潜在变量”。传统上，观察变量用灰色节点表示，而潜在变量用白色节点表示，如上面的图像。我们可能有兴趣找到一些或所有潜在变量的值。

　　回答这些问题类似于机器学习的其他领域的预测 - 在图形模型中，这个过程被称为“推理”。

　　虽然我们使用贝叶斯网络来描述上面的术语，但它也适用于马尔可夫网络。在我们进入学习和推理算法之前，让我们将我们刚才看到的想法形式化 - 给定一些节点的价值，我们可以获得其他节点的信息？

条件独立

　　到目前为止，我们一直在讨论的图形结构实际上捕获了有关变量的重要信息。具体来说，它们定义了变量之间的一组条件独立性，即形式的语句 - “如果观察到A，则B独立于C”。让我们看一些例子。

　　在学生网络中，假设知道学生的SAT成绩很高。你对她的成绩有什么看法？正如我们之前看到的那样，SAT分数高表明学生是聪明的，因此，你会期望学生取得一个好成绩。如果学生的SAT成绩低，该怎么办？在这种情况下，你不会期望学生取得一个好成绩。

　　现在，除了她的SAT成绩外，你还知道学生很聪明。如果SAT成绩很高，那么你会期望得分很高。如果SAT成绩很低怎么办？你仍然期望一个好成绩，因为你知道学生是聪明的，你会认为她只是在SAT上表现不佳。因此，如果我们看到学生的智力，知道SAT分数并不能告诉我们什么。把这作为一个有条件的独立声明，我们会说 - “如果观察到智力，那么SAT和成绩是独立的。”

　　我们从图中这些节点连接的方式获得了这种条件独立信息。如果它们的连接方式不同，我们会得到不同的条件独立信息。

　　让我们看另一个例子。

　　如果你知道这个学生很聪明。你对这门课程的难度有什么看法？简单，对吧？现在，如果我告诉你学生在课程上成绩不好你会怎么想？这表明课程很难，因为聪明的学生成绩都变现的不好。因此，我们可以给出我们的条件独立声明如下 - “如果未观察到等级，那么智力和难度是独立的。”

　　因为这说明了受条件约束的两个节点之间的独立性，所以它们被称为条件独立性。请注意，这两个示例具有相反的语义 ：

• 在第一个示例中，如果观察到连接节点，则独立性成立;
• 在第二个示例中，如果未观察到连接节点，则独立性成立。

　　这种差异是因为节点的连接方式，即箭头的方向。

　　在马尔可夫网络中，我们可以使用类似的方法，但由于没有方向边（箭头），条件独立语句相对简单 - 如果节点A和B之间没有路径，那么路径上的所有节点都是未被观察到的，然后A和B是独立的。换句话说，如果存在从A到B的至少一条路径，其中所有中间节点都未被观察到，则A和B不是独立的。

贝叶斯网络的应用：Monty Hall Problem

 

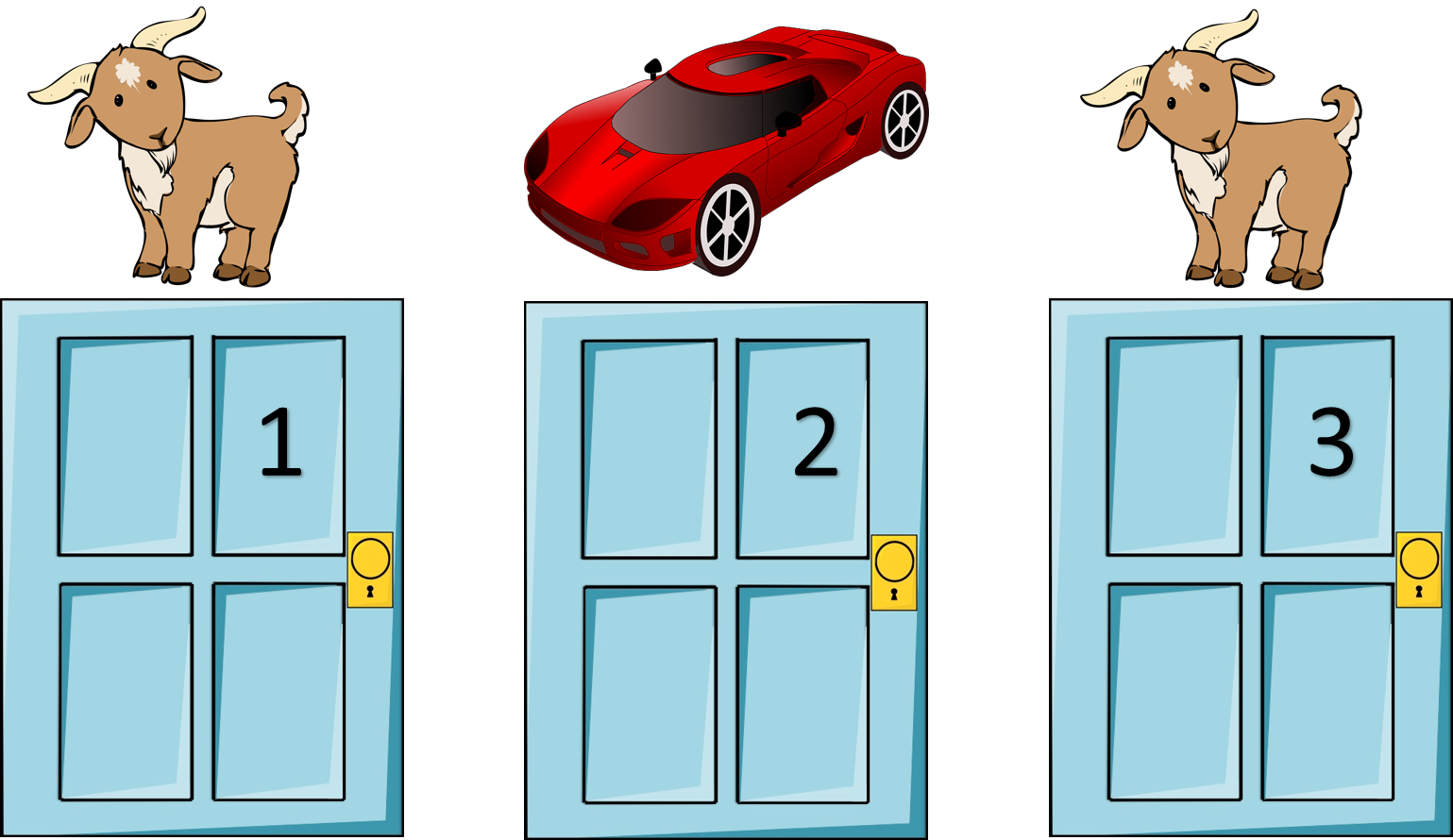
　　主人向你展示了三扇关闭的门，其中一扇门后面有一辆车，而其他门后面则是羊。 你可以选择一扇门。 然后，主机打开剩余的一扇门，并显示它不是汽车。 现在，你可以选择将门从最初选择的门切换到主机未打开的门。 你换了吗？

　　主持人似乎没有透露任何信息，你或许会认为换与不换的赢得车的概率都是$1/2$，然而， 事实证明，这种直觉并不完全正确。 让我们使用 图模型来理解这一点。

让我们从定义一些变量开始：

• D：车门。
• F：你的第一选择。
• H：主持人打开的门。
• I：F = D？

　　D，F和H取值1,2或3，I取0或1.D和I是未观察到的，F是可以观察到的. 在主持人打开其中一扇门之前，H是未被观察到的。 因此，我们为我们的问题获得以下贝叶斯网络：

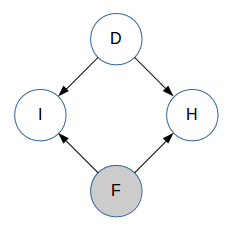
　　注意箭头的方向：D和F是独立的，主持人选择的门H也取决于D和F.到目前为止，你对D一无所知。（这是 类似于学生网络中的结构，在那里了解学生的智慧并没有告诉你关于课程难度的任何信息。）

　　现在，主人拿起一扇门H并打开它。 所以，现在观察到H.

　　观察H并没有告诉我们关于我的任何事情，也不确定我们是否选择了正确的门。  但是，它确实告诉我们一些关于D的事情！ （再次，与学生网络类比，如果你知道学生是聪明的，并且成绩很低，它会告诉你关于课程难度的一些信息。）

　　让我们用数字来看。 变量的CPD表如下（这是在没有观察到变量的情况下）。

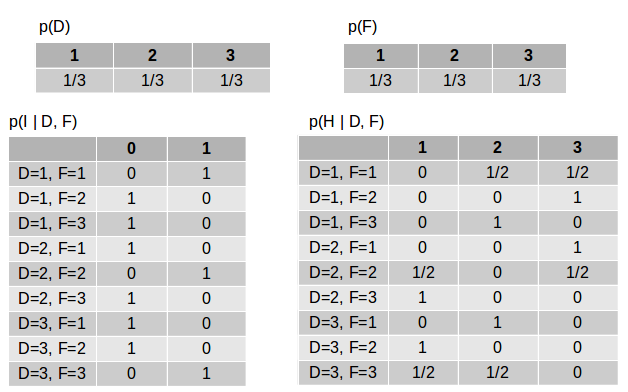
　　D和F的表格很简单 ：我们以相同的概率选择其中一扇门。

　　I表格：当D和F相同时I = 1，而当D和F不同时I = 0。

　　H的表格：如果D和F相等，则主持人以相同的概率从其他两个门中选择一个门，而如果D和F不同，则主持人选择第三个门。

现在，让我们假设我们选择了一扇门，即现在观察到F，比如说F = 1。 给定F，I和D的条件概率是多少？

 

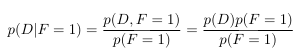
我们可以得到：

 

　　到目前为止，我们选择正确门的可能性是$1/3$。

　　现在，主人打开除F之外的其中一扇门，所以我们观察H.假设H = 2。 让我们计算给定F和H的I和D的新条件概率。

 

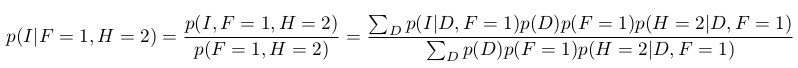
概率分布：

　　因此，当我们一无所知 ： 我们的第一选择仍然是正确的概率$1/3$，这就是我们的直觉告诉我们的。 但是，我们现在知道汽车在门3后面的概率为2/3，而不是1/3。

　　因此，如果我们切换，我们得到的车概率为2/3; 如果我们不这样做，我们会以概率1/3获得汽车。

　　我们可以在不使用图形模型的情况下得到相同的答案，但图形模型为我们提供了一个可以很好地扩展到更大问题的框架。

小结
　　至此，我们研究了图模型中的一些基本术语，包括贝叶斯网络，马尔可夫网络，条件概率分布，潜在函数和条件独立性。 我们还研究了Monty Hall问题的图模型应用。

　　下边，我将介绍参数估计和推理，并给出另一个应用案例。

参数估计
贝叶斯网络
　　估计贝叶斯网络的CPD表中的数字仅等于计算该事件在我们的训练数据中发生的次数。也就是说，为了估计$p（SAT = s^1 | Intelligence = i^1）$，我们只计算$SAT = s^1$和$Intelligence = i^1$的数据点的概率，这些点是离散的，很容易计算。

马尔可夫网络
　　遗憾的是，对于马尔可夫网络，上述计数方法没有统计学证明（因此会导致次优参数）。因此，我们需要使用更复杂的技术。大多数技术背后的基本思想是梯度下降 ：我们定义描述概率分布的参数，然后使用梯度下降来找到这些参数的值，以最大化观测数据的可能性。

　　最后，既然我们有模型的参数，我们想在新数据上使用它们来进行推理与验证！

推理
　　概率图模型中的大部分文献都侧重于推理。 原因有两方面：

• 能够根据我们已经知道的内容进行预测。
• 推理在计算上很难！ 在某些特定类型的图中，我们可以相当有效地执行推理，但在一般图上，它是难以处理的。 因此，我们需要使用近似算法来牺牲准确性以提高效率。

我们可以通过推理解决几个问题：

• 边际推断（Marginal inference）：查找特定变量的概率分布。 例如，给定具有变量A，B，C和D的图，其中A取值1,2和3，求$p（A = 1）$，$p（A = 2）$和$p（A = 3）$的值。
• 后验推断（Posterior inference）：给定一些观察到的变量$v_E$（E代表证据）取值e，找出一些隐藏变量v_H的后验分布$p（v_H | v_E = e）$。
• 最大后验推断（Maximum-a-posteriori (MAP) inference）：给定一些观察到的变量$v_E$，其取值e，寻找其他变量的最高概率$v_H$的值。

　　在下文中，我将介绍一些用于回答这些问题的流行算法，包括精确算法和近似算法。 所有这些算法都适用于贝叶斯网络和马尔可夫网络。

变量消除
使用条件概率的定义，我们可以将后验分布写为：

 

让我们看看如何使用一个简单的例子来计算上面的分子和分母。 考虑具有三个变量的网络，联合分布定义如下：

 

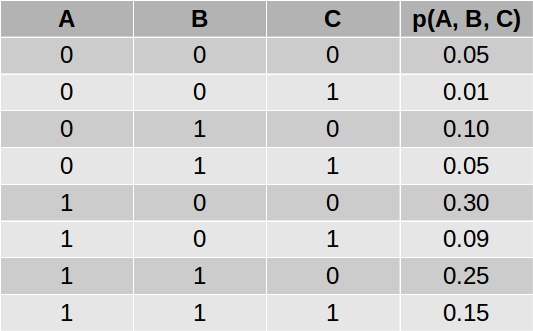
 　　假设我们想要计算$p（A | B = 1）$，这意味着我们想要计算$p（A = 0 | B = 1）$和$p（A = 1 | B = 1）$的值，它们应该总和为1。 使用上面的等式，我们可以写成：

 

　　分子是$A = 0$和$B = 1$的概率。我们不关心C的值。所以我们将C的所有值相加，由于 $p（A = 0，B） = 1，C = 0）$和$p（A = 0，B = 1，C = 1）$是相互排斥的事件，因此它们的并集$p（A = 0，B = 1）$只是各个概率的总和。

　　我们添加第3行和第4行来得到$p（A = 0，B = 1）= 0.15$。类似地，添加行7和8给出$p（A = 1，B = 1）= 0.40$。此外，我们可以通过对包含$B = 14$的所有行（即，行3,4,7和8）求和来计算分母，以得到$p（B = 1）= 0.55$。我们可以计算：

$$p（A = 0 | B = 1）= 0.15 / 0.55 = 0.27$$

$$p（A = 1 | B = 1）= 0.40 / 0.55 = 0.73$$

　　如果你仔细研究上面的计算，你会注意到我们做了一些重复的计算 - 添加第3和第4行，以及第7和第8行两次。计算$p（B = 1）$的更有效方法是简单地计算$p（A = 0，B = 1）$和$p（A = 1，B = 1）$。这是变量消除的基本思想。

　　通常，当你有很多变量时，你不仅可以使用分子的值来计算分母，而且如果仔细观察，分子本身将包含重复的计算。您可以使用动态编程来有效地使用预先计算的值。

　　我们一次对一个变量求和，从而消除它，所以求出多个变量的过程相当于一次一个地消除这些变量。因此，名称“变量消除”。

　　扩展上述过程以解决边际推断或MAP推理问题也很简单。类似地，很容易概括上述想法以将其应用于马尔可夫网络。

　　变量消除的时间复杂度取决于图形结构以及消除变量的顺序。在最坏的情况下，它时间复杂度呈指数递增。

信仰传播
　　我们刚刚看到的VE算法只给出了一个最终分布。 假设我们想要找到所有变量的边际分布。 我们可以做更聪明的事情，而不是多次运行变量消除。

　　假设你有一个图形结构。 要计算边际，需要将联合分布与所有其他变量相加，这相当于汇总整个图形中的信息。 这是从整个图中聚合信息的另一种方法 - 每个节点查看其邻居，并在本地近似变量的分布。

　　然后，每对相邻节点彼此发送“消息”，其中消息包含本地分布。 现在，每个节点查看它接收的消息，并聚合它们以更新其变量的概率分布。

 

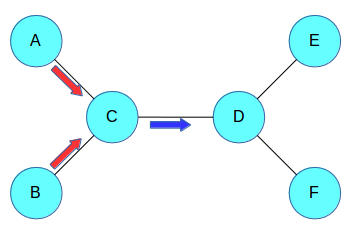
　　在上图中，C聚合来自其邻居A和B的信息，并向D发送消息。然后，D将此消息与来自E和F的信息聚合在一起。

　　这种方法的优点是，如果保存在每个节点上发送的消息，则消息的一个正向传递和一个反向传递将为所有节点提供有关所有其他节点的信息。

　　如果图形不包含循环，则此过程在前向和后向传递之后收敛。如果图形包含循环，则此过程可能会或可能不会收敛，但它通常可用于获得近似答案。

近似推断
　　由于精确推断对于大型图形模型而言可能非常耗时，因此已经为图形模型开发了许多近似推理算法，其中大多数算法属于以下两类之一：

抽样方法
　　这些算法使用抽样估计概率。举一个简单的例子，考虑以下情况 - 给出一个硬币，你如何确定掷硬币时获得头部的概率？最简单的事情就是将硬币翻转100次，然后找出你得到头部的投掷比例。

　　这是一种基于抽样的算法来估计头部的概率。对于概率图形模型中的更复杂问题，可以使用类似的过程。基于采样的算法可以进一步分为两类。在第一个中，样本彼此独立，如上面的硬币投掷示例中所示。这些算法称为蒙特卡罗方法。

　　对于许多变量的问题，生成高质量的独立样本很困难，因此，我们生成相关样本，即每个新样本是随机的，但接近最后一个样本。这种算法称为马尔可夫链蒙特卡罗（MCMC）方法，因为样本形成“马尔可夫链”。一旦我们有样本，我们可以用它们来回答各种推理问题

变分方法
　　变分方法不是使用采样，而是尝试分析地近似所需的分布。 假设你写出用于计算利息分布的表达式 - 边际概率分布或后验概率分布。

　　通常，这些表达式中的积分在计算上很难准确评估。 近似这些表达式的一种好方法是求解替代表达式，并以某种方式确保此替换表达式接近原始表达式。 这是变分方法背后的基本思想。

　　当我们尝试估计复杂概率分布p_complex时，我们定义一组单独的概率分布P_simple，它们更容易使用，然后从P_simple中找到最接近p_complex的概率分布p_approx。

应用：图像去噪
　　假设你有以下图片：

现在假设它被随机噪声破坏了，所以你的嘈杂图像看起来如下：

　　目标是去除图像噪声。让我们看看我们如何使用概率图模型来做到这一点。

　　第一步是考虑我们观察到的和未观察到的变量是什么，以及我们如何将它们连接起来形成图形。让我们将噪声图像中的每个像素定义为观察到的随机变量，并将实况图像中的每个像素定义为未观察到的变量。因此，如果图像是M×N，则存在MN个观测变量和MN个未观测变量。让我们将观察到的变量表示为$X_{ij}$，将未观察到的变量表示为$Y_{ij}$。每个变量取值+1和-1（分别对应于黑色和白色像素）。给定观察到的变量，我们希望找到未观察到的变量的最可能值。这对应于MAP推断。

　　现在，让我们使用一些领域知识来构建图结构。显然，噪声图像中位置$（i，j）$处的观测变量取决于实际图像中位置$（i，j）$处的未观测变量。这是因为大部分时间它们是相同的。

　　对于原始图像，相邻像素通常具有相同的值 -在颜色变化的边界处不是这样的，但在单色区域内，此属性成立。因此，如果它们是相邻像素，我们连接$Y_{ij}$和$Y_{kl}$。

　　因此，我们的图形结构如下所示：

 

　　白色节点表示未观测到的变量$Y_{ij}$，灰色节点表示观测变量$X_{ij}$。 每个$X_{ij}$连接到相应的$Y_{ij}$，每个$Y_{ij}$连接到它的临近节点。

　　这是马尔可夫网络，因为图像的像素之间没有因果关系，因此，在这里定义贝叶斯网络中的箭头方向是不合适的。

　　我们的MAP推理问题可以用数学方法，如下：

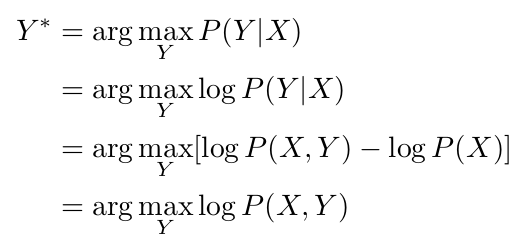
　　我们使用了一些在最大对数似然计算中常见的标准简化技术。 我们将使用X和Y（没有下标）分别表示所有$X_{ij}$和$Y_{ij}$值的集合。

　　现在，我们需要根据图形结构定义联合分布$P（X，Y）$。 假设$P（X，Y）$由两种因子组成:$\phi（X_{ij}，Y_{ij}）$和$\phi（Y_{ij}，Y_{kl}）$，对应于图中的两种边。 接下来，我们定义如下因素：

　　$\phi（X_{ij}，Y_{ij}）= exp（{w_e* X_{ij} ,Y_{ij}）$，其中$w_e$是大于零的参数。

　　当$X_{ij}$和$Y_{ij}$相同时，该因子取大值，当$X_{ij}$和$Y_{ij}$不同时取小值。

　　$\phi（Y_{ij}，Y_{kl}）= exp（w_s*Y_{ij} ,Y_{kl}）$，其中$w_s$是大于零的参数，如前所述。该因子有利于$Y_{ij}$和$Y_{kl}$的相同值。　　

　　因此，我们的联合分发由下式给出：

 

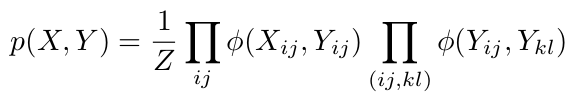
　　其中第二乘积中的$（i，j）$和$（k，l）$是相邻像素，Z是归一化常数。

　　将其代入我们的MAP推理方程给出：

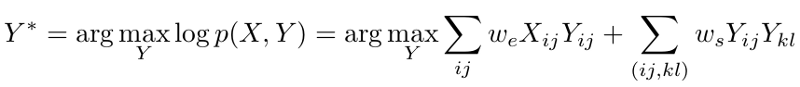
　　使用参数估计技术从地面实况和噪声图像对获得w_e$和$w_s$的值。这个过程在数学上是相当复杂的，因此，我们不会在这里深入研究它。我们假设我们已经获得了以下这些参数的值 :$ w_e = 8$和$w_s = 10$。

　　这个例子的主要焦点是推理。鉴于这些参数，我们想要解决上面的MAP推理问题。我们可以使用置信传播的变体来做到这一点，但事实证明，对于具有这种特定结构的图，有一种更简单的算法称为迭代条件模式（ICM）。

　　基本思想是在每一步中，选择一个节点$Y_{ij}$，查看$Y_{ij} = -1$和$Y_{ij} = 1$的MAP推理表达式的值，并选择具有更高值的节点。重复此过程一定数量的迭代或直到收敛通常合理地工作。

　　去除之后的图像：

 

　　当然，你可以在图形模型和外部使用更多花哨的技术来生成更好的东西，但是从这个例子中可以看出，带有简单推理算法的简单马尔可夫网络已经为你提供了相当不错的结果。python代码

总结：

 　　我们研究了概率图模型中的一些核心思想。图模型提供了一种可解释的方式来模拟许多真实世界的任务，其中存在依赖关系。使用图形模型为我们提供了一种以原则方式处理此类任务的方法。