超平面与法向量

超平面

常见的平面概念是在三维空间中定义的：$Ax+By+Cz+D=0$，
而d维空间中的超平面由下面的方程确定：$w^Tx+b=0$，其中,w与x都是d维列向量$,x=(x_1,x_2,…,x_d) $为平面上的点, $w(w_1,w_,\dots,w_d)$为平面的法向量。$b$是一个实数, 代表平面与原点之间的距离.

点到超平面的距离：

假设点x′为超平面$A：w^Tx+b=0$上的任意一点, 则点$x$到$A$的距离为$x−x'$在超平面法向量$w$上的投影长度：

$$d=\frac{|w^T(x-x')|}{||w||}=\frac{|w^Tx+b|}{||w||}$$

超平面的正面与反面：

一个超平面可以将它所在的空间分为两半, 它的法向量指向的那一半对应的一面是它的正面, 另一面则是它的反面。

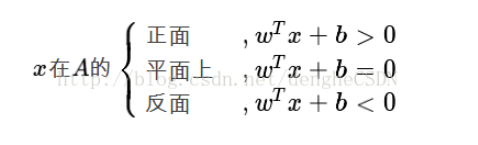
若将距离公式中分子的绝对值去掉, 让它可以为正为负. 那么, 它的值正得越大, 代表点在平面的正向且与平面的距离越远. 反之, 它的值负得越大, 代表点在平面的反向且与平面的距离越远。

 

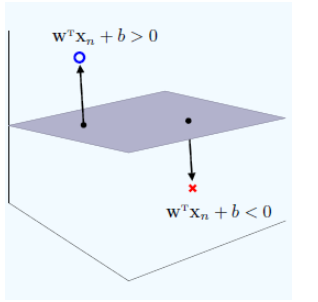
 法向量的意义

 

在空间里，向量可以看做是一个点（以原点为起始点的向量），对于分离超平面方程里的向量$x$，就可以看做由坐标原点到超平面任意“点”的向量，法向量的大小是坐标原点到分离超平面的距离，垂直于分离超平面，方向有分离超平面决定。

支持向量机的一些理解

首先如果超平面的形式为:$w_1x_1+w_2x_2+\cdots+w_Nx_N+b=0$,向量化表示为：$w^Tx+b=0$

Notes:

  统一超平面的形式：即在$w$,$b$同时扩大或缩小相同倍数后得到不同的超平面形式，但其实代表同一超平面。此时可以通过找到离这条直线最近的点$x_0$，方程两边同时除以$w^Tx+b$，注意离超平面最近的点使得$w^Tx+b=1$，其他的点都是$w^Tx+b\geqslant 1$，再利用样本的标签+1,−1使得到的超平面方程统一化。此时数据集到求出的超平面的最短距离是$\frac{1}{||w||}$