决策树（二）关于的决策树的一些思考

1.基于树的模型比线性模型更好吗？

　　如果我可以使用逻辑回归解决分类问题和线性回归解决回归问题，为什么需要使用树模型？ 我们很多人都有这个问题。 实际上，你可以使用任何算法。 这取决于你要解决的问题类型。 其中有一些关键因素，它们将帮助你决定使用哪种算法：

• 如果因变量和自变量之间的关系通过线性模型很好地近似，则线性回归将优于基于树的模型。
• 如果因赖变量和自变量之间存在高度非线性和复杂关系，则树模型将优于经典回归方法。
• 如果你需要构建一个易于向人们解释的模型，决策树模型总是比线性模型更好。 决策树模型甚至比线性回归更容易解释！

2.树建模的关键参数是什么？如何避免决策树过度拟合？

　　过度拟合是决策树建模时面临的主要挑战之一。 如果没有限制，它将为您提供100％的训练集准确性，因为在最坏的情况下，它最终会为每个观察结果制作1片叶子。 因此，在对决策树进行建模时，防止过度拟合是关键，可以通过两种方式完成：

• 设置树大小的约束
• 树修剪（Tree pruning）

让我们简单地讨论这两个问题。

设置树大小的约束

这可以通过使用用于定义树的各种参数来完成。 首先，让我们看一下决策树的一般结构：

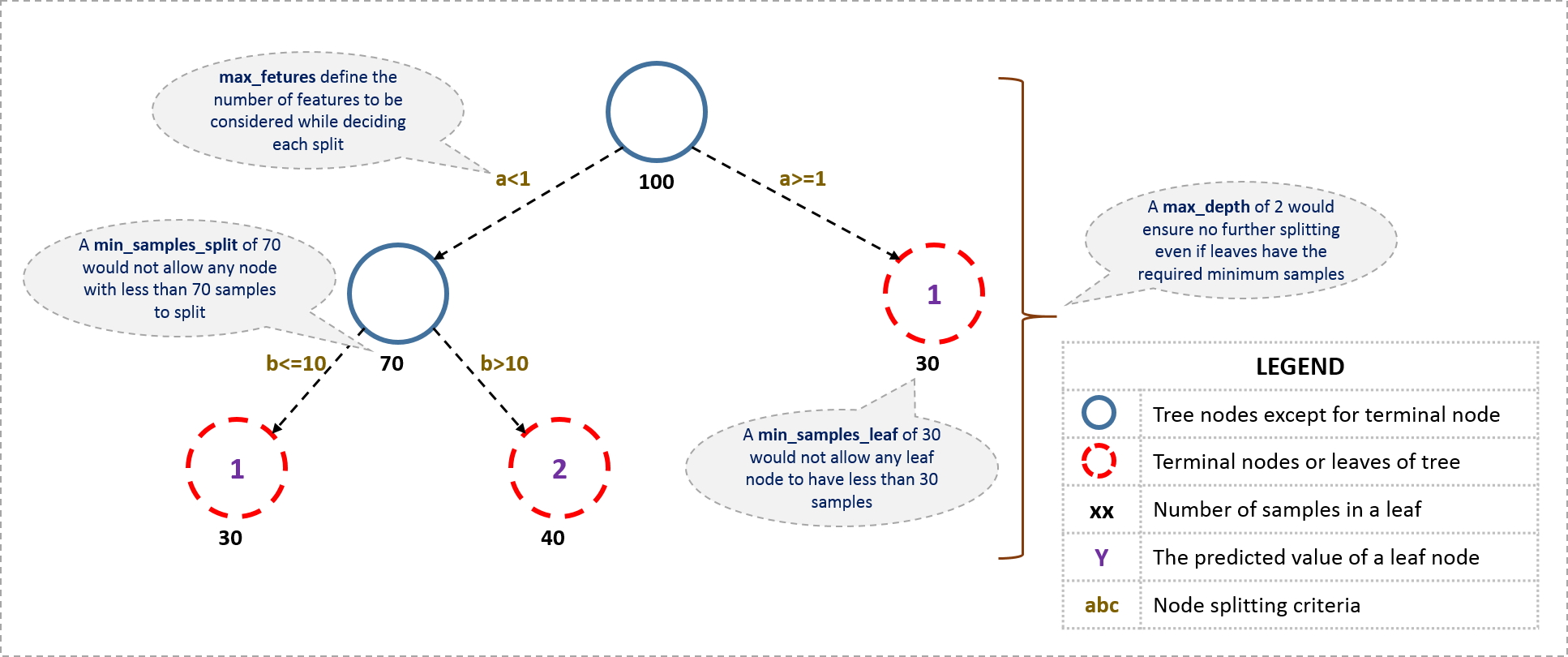
• 1.节点拆分的最小样本（Minimum samples for a node split）
• 定义要考虑拆分的节点中所需的最小样本数（或观察数）。
• 用于控制过度配合。 较高的值会阻止模型学习关系，这种关系可能对为树选择的特定样本高度特定。
• 太高的值会导致欠拟合，因此应使用CV（calculate Variance）进行调整。

• 2.终端节点的最小样本（叶子）（ Minimum samples for a terminal node (leaf)）

• • 定义终端节点或叶子中所需的最小样本（或观察值）。
  • 用于控制过度拟合，类似于min_samples_split。
  • 一般来说，应该选择较低的值来解决不平衡的阶级问题，因为少数群体占多数的地区将占很大比例。

• 3最大树木深度（垂直深度）（Maximum depth of tree (vertical depth)）

• • 树的最大深度。
  • 用于控制过度拟合，因为更高的深度将允许模型学习非常特定于特定样本的关系。
  • 应该使用CV进行调整。

• 4.最大终端节点数（Maximum number of terminal nodes）

• • 树中终端节点或叶子的最大数量。
  • 可以定义代替max_depth。 由于创建了二叉树，因此深度'n'将产生最多2 ^ n个叶子。

• 5.拆分时要考虑的最大特征（Maximum features to consider for split）

• • 搜索最佳拆分数量时要考虑的特征数量，这些特征应该被随机选择。
  • 功能总数的平方根效果很好，但我们应该检查特征总数的30-40％。
  • 较高的值可能导致过度拟合。

树修剪（Tree pruning）

　　通过修剪可以进一步提高树的性能。 它删除不重要性的特征的分支， 这样，我们降低了树的复杂性，从而通过减少过度拟合来提高其预测能力。

修剪可以从根或叶开始。 最简单的修剪方法从叶子开始，并删除该叶子中所属类的每个节点，如果不降低精度，则保持这种变化。 它也称为减少错误修剪。 可以使用更复杂的修剪方法，例如成本复杂性修剪，其中使用学习参数（α）来权衡是否可以基于子树的大小来移除节点。 这也被称为最薄弱的链接修剪。

CART的优点

• 易于理解，解释，可视化。
• 决策树隐式执行变量筛选或特征选择。
• 可以处理数字和分类数据。还可以处理多输出问题。
• 决策树需要用户用于数据准备的相对较少的努力。
• 参数之间的非线性关系不会影响树性能。

CART的缺点

• 决策树学习者可以创建过于复杂的树，这些树不能很好地推广数据--称为过度拟合。
• 决策树可能不稳定，因为数据中的小变化可能导致生成完全不同的树--称为方差，需要通过bagging和boosting等方法降低。
• 贪婪算法无法保证返回全局最优决策树。这可以通过训练多个树来减轻，如特征和样本随机替换。
• 如果某些类占主导地位，决策树学习者会创建偏向的树。因此，建议在拟合决策树之前平衡数据集。

3.使用什么标准来确定正确的最终树大小？

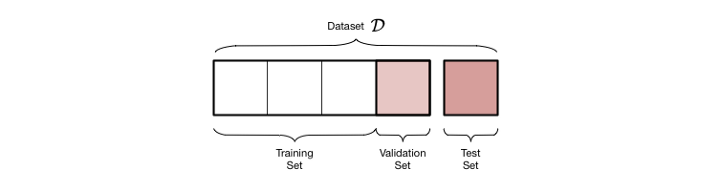
　　在这种方法中，可用数据被分成两组：用于形成学习假设的训练集和用于评估该假设的准确性的单独验证集，特别是用于评估 修剪这个假设的影响。

动机是这样的：即使学习者可能被训练集内的随机错误和巧合规律误导，验证集也不太可能表现出相同的随机波动。 因此，可以预期验证集可以提供针对过度拟合的安全检查。

　　当然，验证集必须足够大，以便自身提供统计上显着的实例样本。 一种常见的启发式方法是保留验证集中可用示例的三分之一，使用其他三分之二进行训练。

4.我们究竟如何使用验证集来防止过度拟合？

　　一种称为减少错误修剪（Quinlan 1987）的方法是将树中的每个决策节点视为修剪的候选者。修剪决策节点包括删除以该节点为根的子树，使其成为叶节点，并为其分配与该节点关联的训练示例的最常见分类。

 

　　仅当生成的修剪树在验证集上执行的情况不比原始情况差时，才会删除节点。迭代地修剪节点，总是选择其移除最多地增加决策树精度而不是验证集的节点。节点的修剪继续，直到进一步修剪是有害的（即，降低树在验证集上的准确性）。

 

 

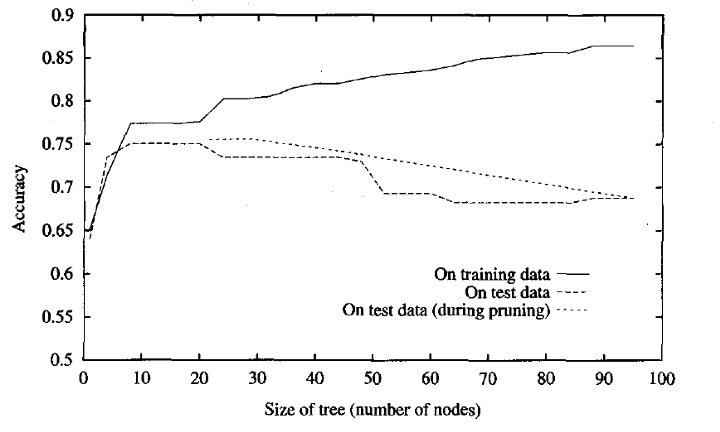
 　　减少错误修剪在决策树学习中的作用：随着节点从树中删除，测试集的准确度会提高。 这里，用于修剪的验证集与训练集和测试集都不同。未显示用于修剪的验证集的准确性。

　　另外，可用数据被分成三个子集：训练样例，用于修剪树的验证示例，以及一组用于在未来看不见的示例中提供无偏估计精度的测试示例。

如果有大量数据可用，则使用一组单独的数据来指导修剪是一种有效的方法。一种常见的启发式方法是：训练集占所有数据的60％，验证集占20％，测试集占20％。这种方法的主要缺点是，当数据有限时，为验证集扣留部分数据会减少甚至还有可用于培训的例子。