决策树(一)
-
简介
基于树的学习算法被认为是最好的和最常用的监督学习方法之一。 基于树的方法赋予预测模型高精度,稳定性和易于解释的能力。 与线性模型不同,它们非常好地映射非线性关系。 它们适用于解决手头的任何问题(分类或回归)。决策树,随机森林,梯度增强等方法正在各种数据科学问题中广泛使用。 因此,对于每个分析师学习这些算法并将其用于建模非常重要。本文的目的是介绍决策树学习的基本理论基础,并提出ID3算法。
什么是决策树?
简而言之,决策树是一棵树,其中每个分支节点代表多个备选方案之间的选择,每个叶节点代表一个决策。它是一种监督学习算法,主要用于分类问题,适用于分类和连续输入和输出变量。 是归纳推理的最广泛使用和实用的方法之一(归纳推理是从具体例子中得出一般结论的过程)。决策树从给定的例子中学习和训练数据,并预测不可见的情况。
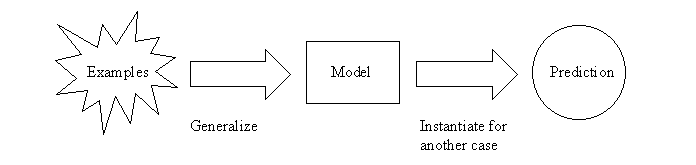
决策树的图形表示可以是:

有几种算法可以构建决策树,其中一些是:
- CART(分类和回归树):使用基尼指数作为度量。
- ID3算法:使用熵函数和信息增益作为度量。
在本文中,我们将重点关注ID3算法。
与决策树相关的重要术语
基本术语:
- 根节点(Root Node):它代表整个种群或样本,并进一步分为两个或更多个同类集。
- 拆分(Splitting):这是将节点划分为两个或更多个子节点的过程。
- 决策节点(Decision Node):当子节点分裂成更多的子节点时,它被称为决策节点。
- 叶子/终端节点(Leaf/ Terminal Node):不分割的节点称为叶子或终端节点。
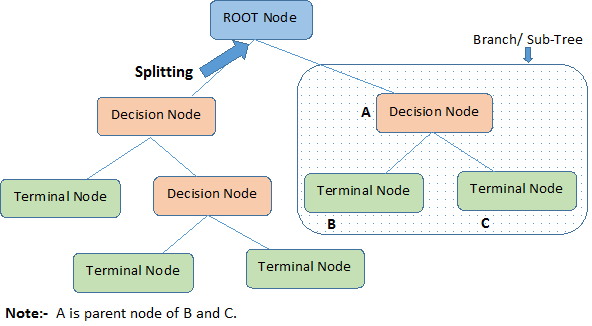
- 修剪(Pruning):当我们删除决策节点的子节点时,此过程称为修剪。 你可以说相反的分裂过程。
- 分支/子树(Branch / Sub-Tree):整个树的子部分称为分支或子树。
- 父节点和子节点(Parent and Child Node):划分为子节点的节点称为子节点的父节点,其中子节点是父节点的子节点。
分类VS回归
当因变量是连续的时,使用回归树。因变量是分类时使用分类树。
- 在回归树的情况下,训练数据中终端节点获得的值是落在该区域中的观测的平均值。因此,如果看不见的数据观观测属于该区域,我们将使用平均值进行预测。
- 在分类树的情况下,终端节点在训练数据中获得的值(类)是落在该区域中的观察模式。因此,如果看不见的数据观察属于该区域,我们将使用模式值进行预测。
两棵树都将预测空间(自变量)划分为不同的和不重叠的区域。为简单起见,您可以将这些区域视为框。
这两棵树都遵循自上而下的贪婪方法,称为递归二进制分裂。我们将其称为“自上而下”,因为当所有观察在单个区域中可用时,它从树的顶部开始,并且连续地将预测器空间分成树下的两个新分支。它被称为“贪婪”,因为该算法只关注当前分裂的关键(寻找最佳可用变量),而不关心将来会导致更好树的分裂。继续该拆分过程,直到达到用户定义的停止标准。例如:一旦每个节点的观测数量小于50,我们就可以告诉算法停止。
在这两种情况下,分裂过程都会导致树木完全生长,直到达到停止标准。但是,完全成长的树可能会过度填充数据,导致看不见的数据的准确性很差。这带来了'修剪'。修剪是用于解决过度拟合的技术之一。
优点
- 易于理解:即使对于非分析背景的人来说,决策树输出也很容易理解。它不需要任何统计知识来阅读和解释它们。它的图形表示非常直观。
- 在数据探索中很有用:决策树是识别最重要变量和两个或多个变量之间关系的最快方法之一。在决策树的帮助下,我们可以创建具有更好预测目标变量能力的新变量(特征)。你可以参考一篇文章(Trick to enhance power of regression model)。它也可以用于数据探索阶段。例如,我们正在研究一个问题,即我们有数百个变量可用的信息,决策树将有助于识别最重要的变量。
- 需要更少的数据清理:与其他一些建模技术相比,它需要更少的数据清理。它不受异常值和缺失值的影响。
- 数据类型不是约束:它可以处理数字和分类变量。
- 非参数方法:决策树被认为是非参数方法。这意味着决策树没有关于空间分布和分类器结构的假设。
缺点
- 过拟合:过拟合是决策树模型最实用的难点之一。 通过设置模型参数和修剪的约束来解决这个问题。
- 不适合连续变量:在处理连续数值变量时,决策树在对不同类别的变量进行分类时会丢失信息。
ID3算法
ID3代表Iterative Dichotomizer 3。ID3算法由Ross Quinlan发明。 它从一组固定的实例构建决策树,结果树用于对测试样本进行分类。基本思想是通过在给定集合中使用自上而下的贪婪搜索来构造决策树,以测试每个树节点处的每个属性。决策树的构造是作为重复过程完成的,估计哪个变量可以获得最大的信息增益。信息增益是当已知自变量的状态时因变量的熵的减少。从本质上讲,当我们根据因变量的值将它分成组时,它会测量独立变量的组织程度。选择提供组织最大增加的因变量,并根据此变量拆分数据集。
信息熵(Entropy)
在信息论中,熵是衡量消息来源不确定性的指标。 它为我们提供了数据中的无组织程度。
给定集合S包含某些目标概念的正面和负面示例,S相对于此布尔分类的熵是:

这里,p +和p-是S中正负例子的比例。
考虑相对于布尔分类(即二分类)的这种熵函数,因为正例p +的比例在0和1之间变化。

假设S是14个例子的集合,包括9个正例和5个负例子[9 +,5-]。 然后S的熵是:

请注意,如果S的所有成员属于同一个类,则熵为0。 例如,如果所有成员都是正数(p + = 1),则p-为0,并且
Entropy(S)= -1* log2(1) - 0.*log2 0 = -1. 0 - 0. log2 0 = 0。
当集合包含相同数量的正面和负面示例时,熵为1。
如果集合包含不等数量的正面和负面示例,则熵在0和1之间。
信息增益(Information Gain)
它衡量预期的熵减少。 它决定哪个属性进入决策节点。 为了最小化决策树深度,具有最多熵减少的属性是最佳选择!更确切地说,属性A相对于示例集合S的信息增益增益(S,A)被定义为:
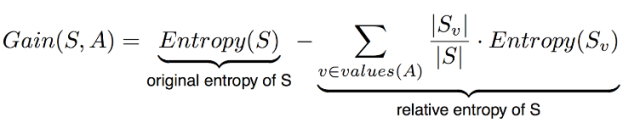
- S =属性A的所有可能值的每个值v
- Sv =属性A具有值v的S的子集
- | SV| = Sv中的元素数
- | S | = S中的元素数
具体例子
假设我们想要ID3来决定天气是否适合打棒球。 在两周的时间内,收集数据以帮助ID3构建决策树。 目标分类是“我们应该打棒球吗?”,可以是或不是。
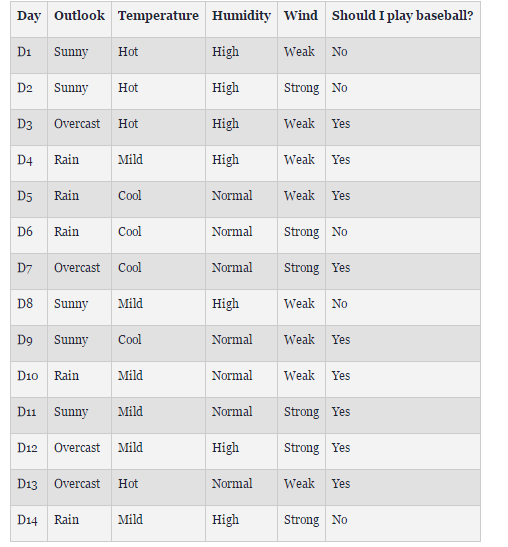
天气属性是 outlook, temperature, humidity, and wind speed.。
-
outlook = { sunny, overcast, rain }
-
temperature = {hot, mild, cool }
-
humidity = { high, normal }
-
wind = { weak, strong }
我们需要找到哪个属性将成为决策树中的根节点。
计算数据集上最高信息增益的步骤
1.计算整个数据集的熵
14个记录,9个yes,5个No
- Entropy(S) = – (9/14) Log2 (9/14) – (5/14) Log2 (5/14) = 0.940
2.计算每个属性熵
2.1 - outlook
outlook属性包含三个 不同的观测:
- outlook = { sunny, overcast, rain }
-
- overcast: 4 个记录, 4 个 “yes”

- rainy: 5 个记录, 3 个 “yes”
-
-
sunny: 5 个几率, 2 个“yes”
- 预期的新熵:
-
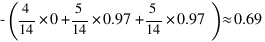
2.2 - temperature

预期的新熵:

2.3 - humidity

预期的新熵:
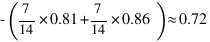
2.4 - windy

预期的新熵:
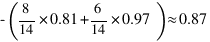
3.信息增益

显然,outlook属性的增益最高。 因此,它用作根节点。
由于outlook有三个可能的值,因此根节点有三个分支( sunny, overcast, rain )。 接下来的问题是,应该在sunny分支节点测试什么属性? 由于我们在根部使用了outlook,我们只决定其余三个属性: temperature, humidity, and wind。
-
Ssunny = {D1, D2, D8, D9, D11} = 5 examples from the table with outlook = sunny
-
Gain(Ssunny, Humidity) = 0.970
-
Gain(Ssunny, Temperature) = 0.570
-
Gain(Ssunny, Wind) = 0.019
humidity,增益最大; 因此,它被用作决策节点。 这个过程一直持续到所有数据都被完美分类或者我们的属性用完了.

决策树也可以用规则格式表示:
- IF outlook = sunny AND humidity = high THEN play baseball = no
- IF outlook = rain AND humidity = high THEN play baseball = no
- IF outlook = rain AND wind = strong THEN play baseball = yes
-
IF outlook = overcast THEN play baseball = yes
- IF outlook = rain AND wind = weak THEN play baseball = yes
最终会生成一颗像下边一样的树:




