SVM简要介绍

SVM

支持向量机（SVM），是一个用于解决二分类问题的有监督机器学习模型。

1.SVM的两个优点

• 更高的速度

• 在有一定的样本数量支持下（成千上万张），具有比其他模型有更好的效果

2.SVM的工作过程

2.1.线性数据

为了更好地理解SVM的工作流程，我们引入一个例子。假如在一个\(xy\)坐标系上有很多红色和蓝色的点，将这些点看作是我们要处理的两个(categories)类别(red,blue)，而我们的数据具有两个(features)特征\(x\)和\(y\)，我们想要找到一个(classifier)判别器，当我们给定一个坐标\((x,y)\)，判别器会给出    该坐标所属的类别\(red\)或\(blue\)，具体描述如下图。



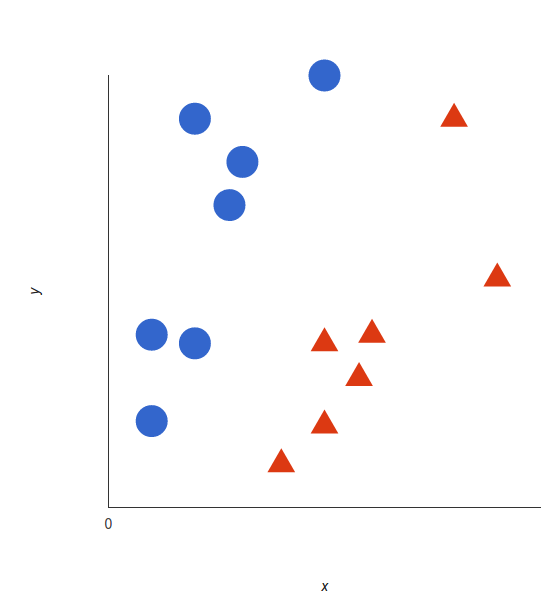
SVM对于以上给定的数据点，能够给出一条最好的划分两个样本的直线，使得直线的一边全部都是\(red\)，另一边全部都是\(blue\)。



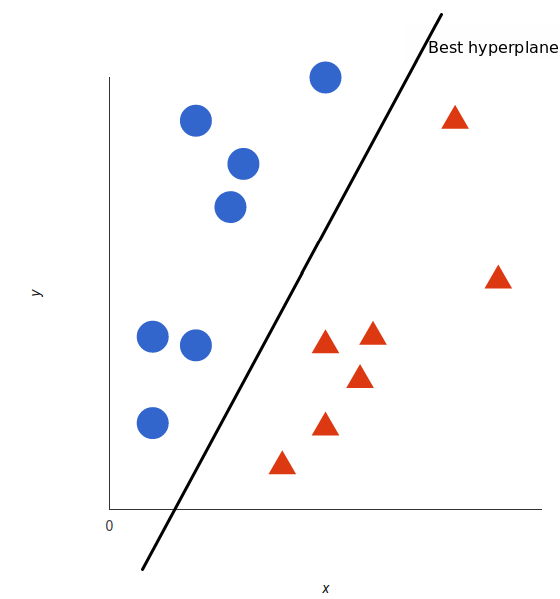
但是，能够划分的直线有无数条，那一条才是最好的呢？对于SVM来说，最好的划分直线就是让两边最近的点离直线的距离最近。如图所示



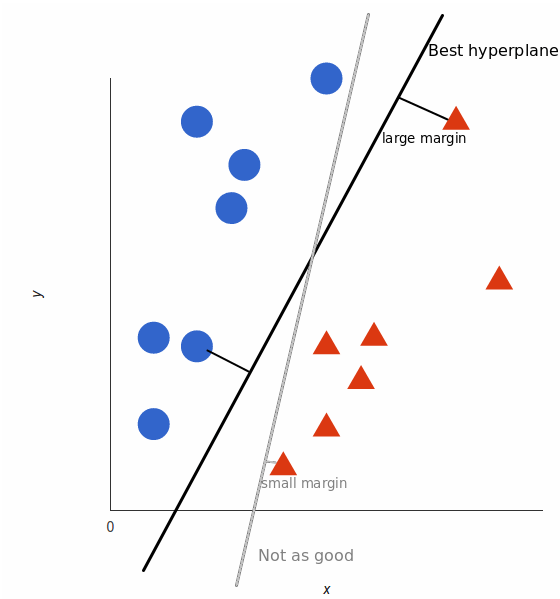
2.2.非线性数据

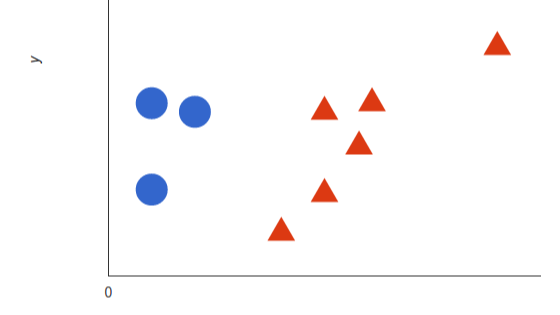
对于线性数据来说，很容易就找到了最优分割线，但对于一些非线性数据来说，用线性分割线来分割就显得比较困难了。如下



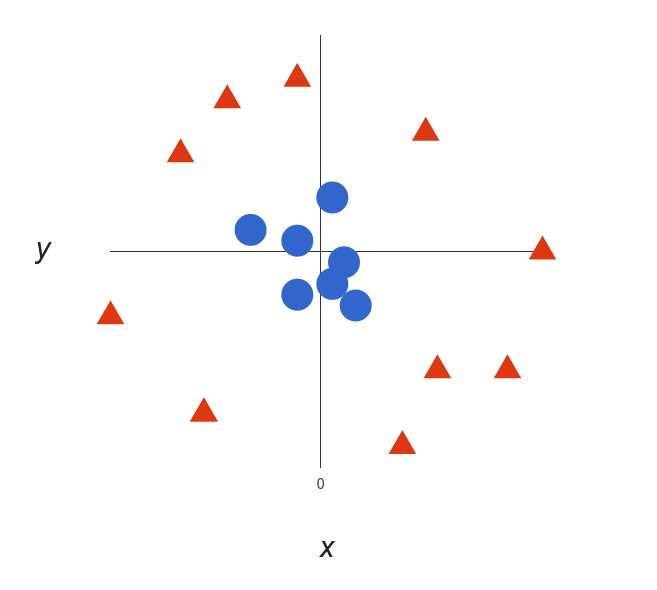
在二位坐标\(xy\)上，想找到一条分割线来进行分割两个类别是非常困难的。所以我们增加一个坐标系\(z\)，我们令\(z=x^2+y^2\)，将原来二维的数据映射到三维空间上，如下图



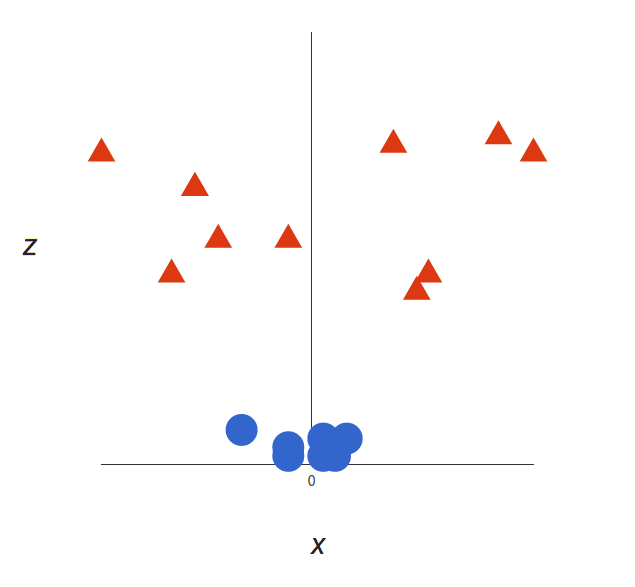
这样，我们就可以巧妙地用一个平面分割两个类别的数据。我们来看一下



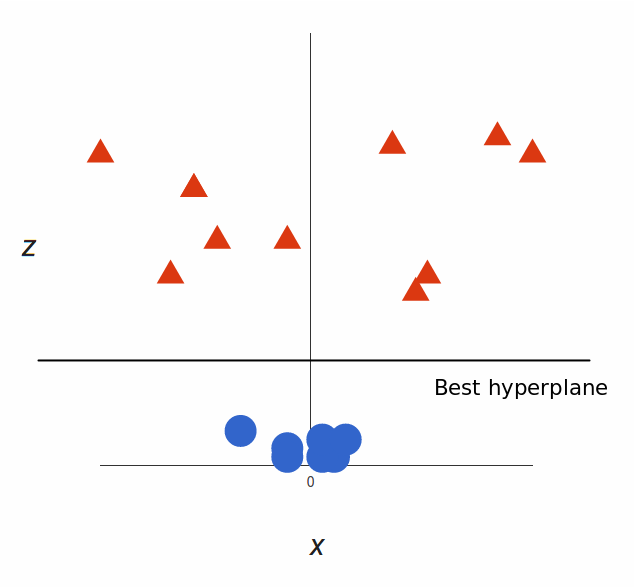
将它重新映射回二位平面上



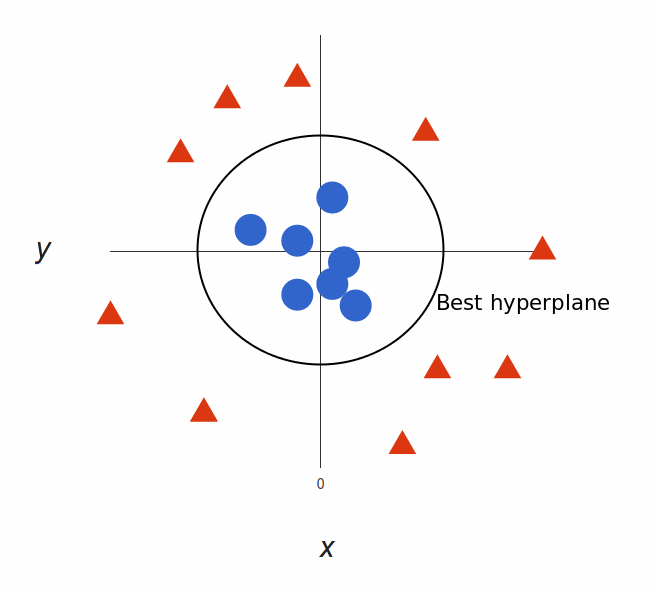
由此，我们就可以轻松地找到一个分割线来分割两个类别

原来是在二维平面上找 \(a · b = xa · xb  +  ya · yb +  (xa² + ya²) · (xb² + yb²)\) 找\(x\)和\(y\)的最优解，转化成在三位空间中找 \(a · b = xa · xb  +  ya · yb  +  za · zb\) 找\(x\)和\(y\)的最优解

所以，对于一些非线性的数据来说，增加一个维度进行计算是SVM常用的方法