美赛速成(附代码)
算法模型详细:
一、层次分析法:
用于解决对要考虑带有不同属性的各个决定因素的决策问题。
如:有三个景点:桂林、苏杭、北戴河
有五个因素:景色、费用、居住、饮食、旅途
要做出决策去哪个地方?

算法求解步骤:
1.求成对比较矩阵
(1)先求5个因素之间的成对比较矩阵
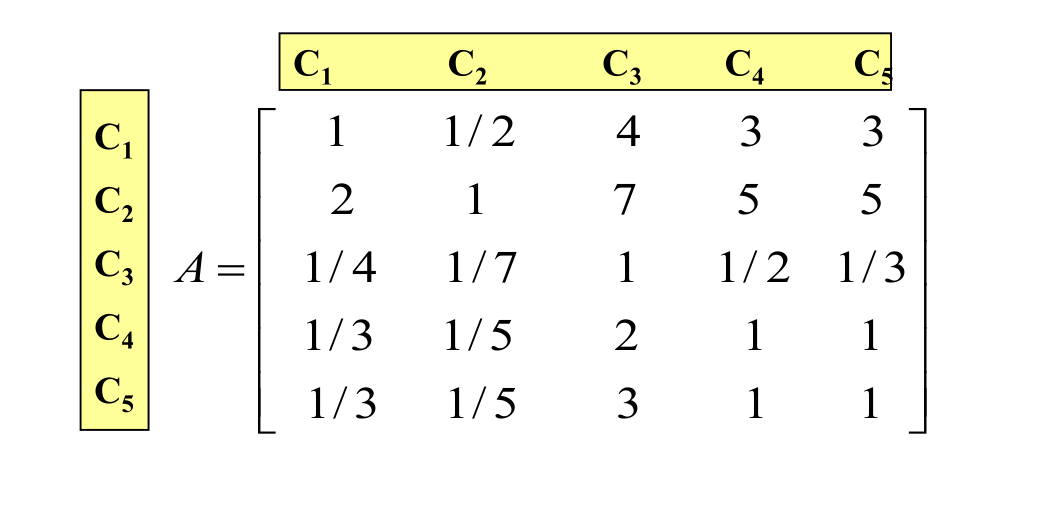
c1~c5表示5个因素,cij表示ci对cj的重要程度是多少?

如:cij=3就是ci比cj稍微重要
(2)再求3个景点分别对于5个因素的5个成对比较矩阵
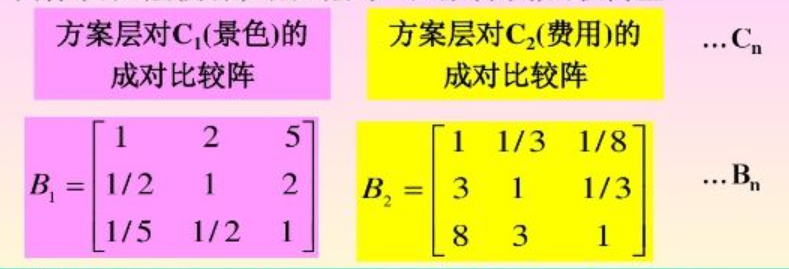
如:在因素1中,b12=3就是对于因素1(景色)来说景点1(桂林)比景点2(苏杭)稍微好
2.分别对求出的成对比较矩阵进行求各自的权重
Matlab代码:
disp('请输入判断矩阵A(n阶)');
A=input('A=');
[n,n]=size(A);
x=ones(n,100);
y=ones(n,100);
m=zeros(1,100);
m(1)=max(x(:,1));
y(:,1)=x(:,1);
x(:,2)=A*y(:,1);
m(2)=max(x(:,2));
y(:,2)=x(:,2)/m(2);
p=0.0001;i=2;k=abs(m(2)-m(1));
while k>p
i=i+1;
x(:,i)=A*y(:,i-1);
m(i)=max(x(:,i));
y(:,i)=x(:,i)/m(i);
k=abs(m(i)-m(i-1));
end
a=sum(y(:,i));
w=y(:,i)/a;
t=m(i);
disp(w);
%以下是一致性检验
CI=(t-n)/(n-1);RI=[0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59];
CR=CI/RI(n);
if CR<0.10
disp('此矩阵的一致性可以接受!');
disp('CI=');disp(CI);
disp('CR=');disp(CR);
end
运行代码时,将成对比较矩阵输入即可
最后输出各自的权重:
操作步骤:
(1)新建一个脚本文件,赋值代码到文件里,保存成.mat文件
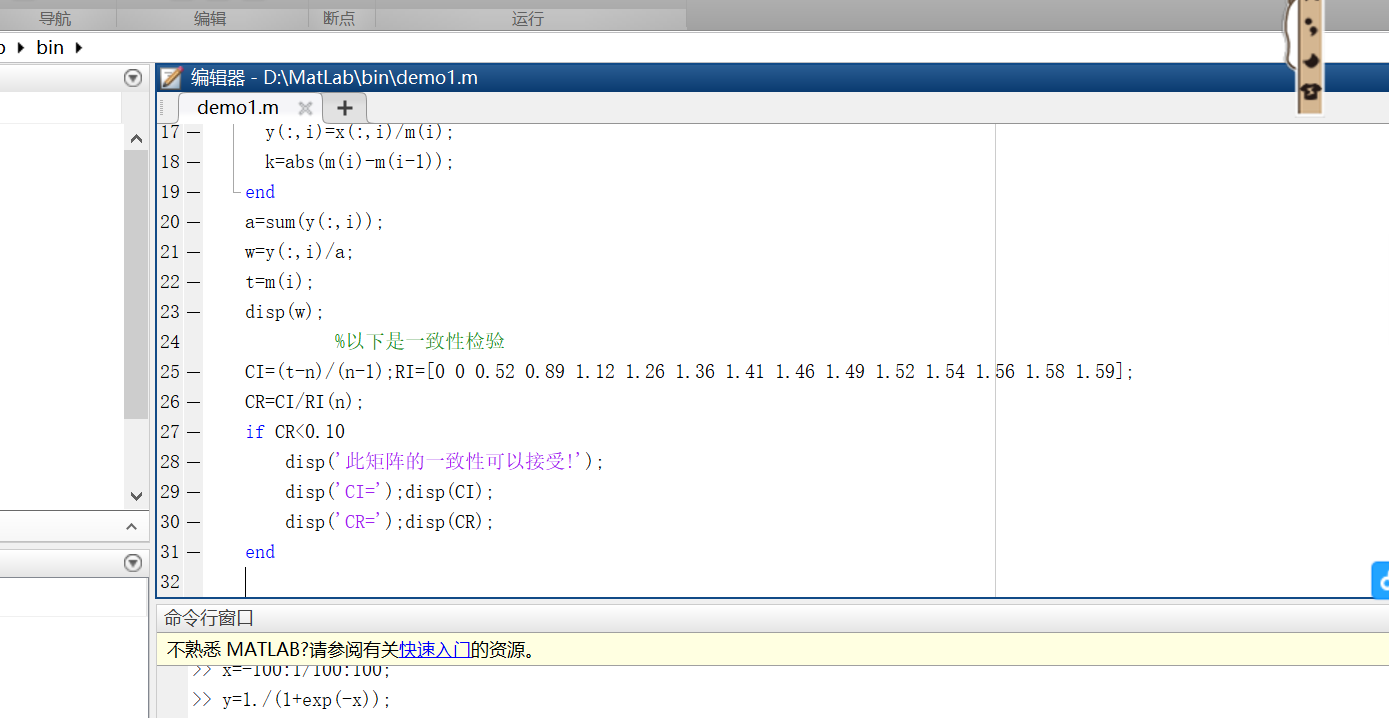
(2)在命令行中输入脚本名,回车运行

(3)输入矩阵,回车运行,得到5行数值,即对应5个因素各自的权重

根据上述步骤求出以下的权重:

3.根据上面求出的权重求3个景点对于总目标的权值
设B1、B2、B3对A1的权值为D1,对A2的权值为D2,...
如:D1A1+D2A2+...+D5*A5就是景点1对总目标的权值

求出3个景点对总目标的权值后,最大权值的方案就是最优方案
所以选景点3
二、多属性决策模型
是利用已有的决策信息通过一定的方式对一组(有限个) 备选方案进行排序或择优。
在介绍多属性决策模型之间,我们先来介绍一下归一化:
归一化:
若有一组数据[a1,a2,a3,a4]
如果这些数据是有益的(如:收入、盈利等),则归一化之后的数据为[a1/max(a),a2/max(a),a3/max(a),a4/max(a4)]
如果这些数据是有害的(如:亏损、丢失等),则归一化之后的数据为[min(a)/a1,min(a)/a2,min(a)/a3,min(a)/a4]
下面开始介绍多属性决策模型:
1.先用已有数据进行实例化
例如:投资银行拟对某市4家企业(方案) 进行投资,抽取下列5项指标(属性)进行评估:
—产值(万元);
—投资成本(万元);
—销售额(万元);
—国家收益比重;
—环境圬染程度。
用给定的数据实例化:
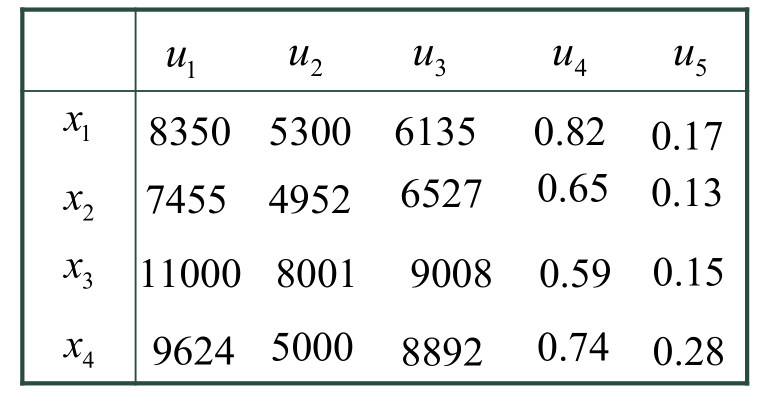
x1x4:4所公司,u1u5:5个因素
表示每所公司对每个因素的实际值
2.将上面得到的值进行归一化
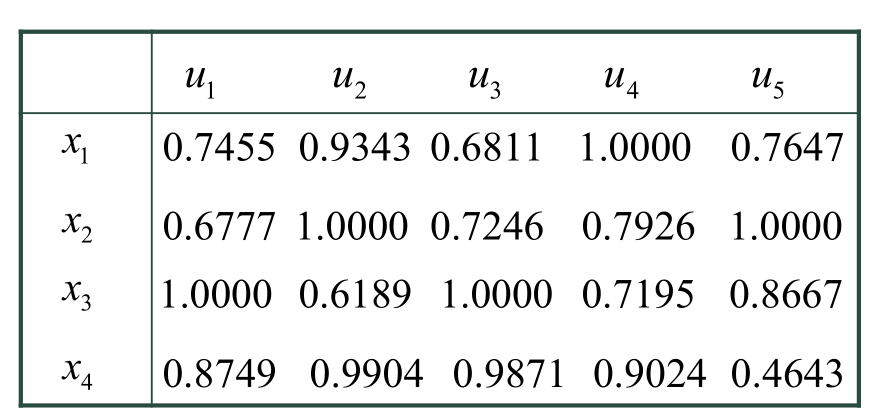
3.用层次分析法中的方法求5个因素组成的成对分析矩阵
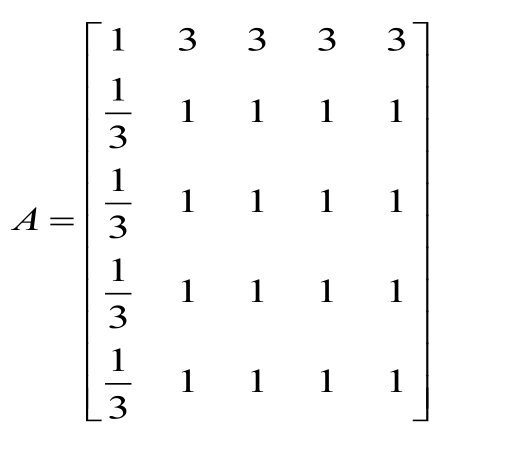
4.求出成对分析矩阵的各个因素的权值
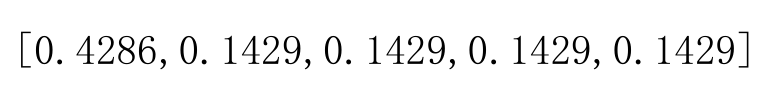
5.求待决策量对总目标的权值
具体方法就不说了,大家看图吧,waa就是最后的权重
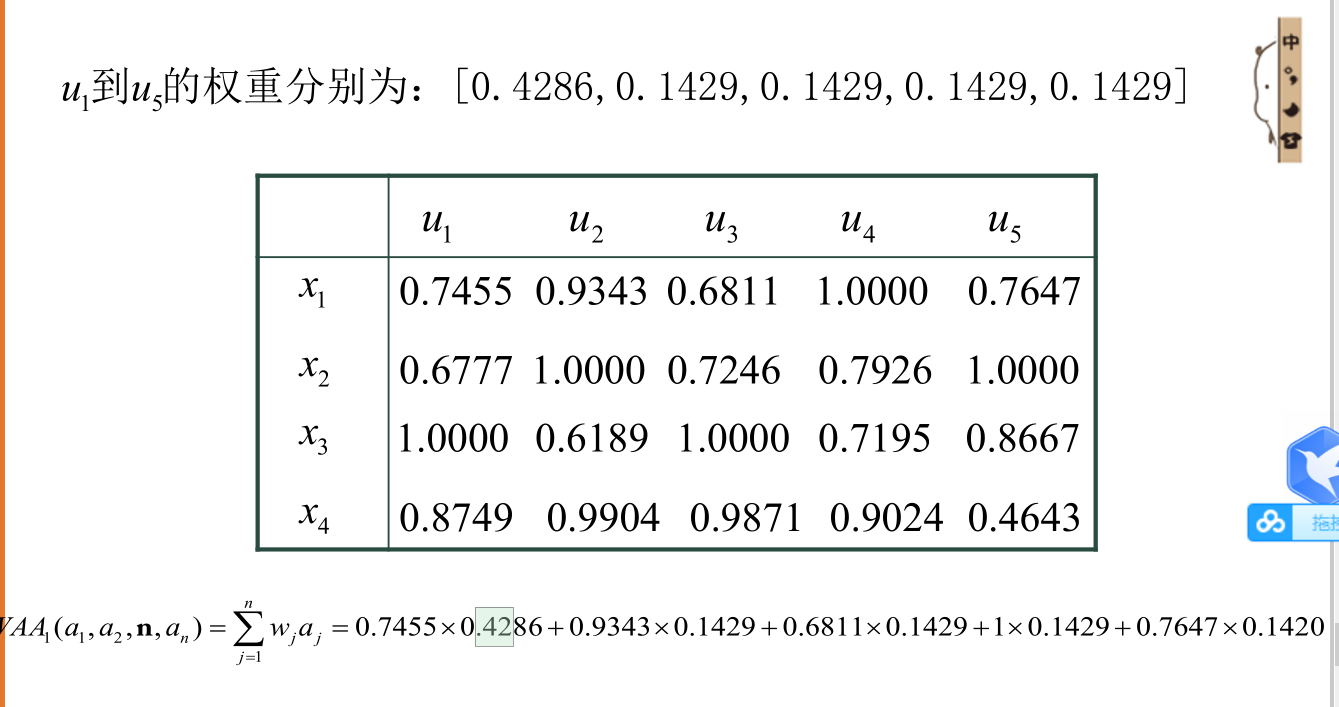
求出4个企业的权值

所以选企业3
三、灰色预测模型
这个就是一个曲线拟合再预测的模型
这个原理就不说了,直接上代码吧
function []=greymodel(y)
% 本程序主要用来计算根据灰色理论建立的模型的预测值。
% 应用的数学模型是 GM(1,1)。
% 原始数据的处理方法是一次累加法。
y=input('请输入数据 ');
n=length(y);
yy=ones(n,1);
yy(1)=y(1);
for i=2:n
yy(i)=yy(i-1)+y(i);
end
B=ones(n-1,2);
for i=1:(n-1)
B(i,1)=-(yy(i)+yy(i+1))/2;
B(i,2)=1;
end
BT=B';
for j=1:n-1
YN(j)=y(j+1);
end
YN=YN';
A=inv(BT*B)*BT*YN;
a=A(1);
u=A(2);
t=u/a;
i=1:n+2;
yys(i+1)=(y(1)-t).*exp(-a.*i)+t;
yys(1)=y(1);
for j=n+2:-1:2
ys(j)=yys(j)-yys(j-1);
end
x=1:n;
xs=2:n+2;
yn=ys(2:n+2);
plot(x,y,'^r',xs,yn,'*-b');
det=0;
sum1=0;
sumpe=0;
for i=1:n
sumpe=sumpe+y(i);
end
pe=sumpe/n;
for i=1:n;
sum1=sum1+(y(i)-pe).^2;
end
s1=sqrt(sum1/n);
sumce=0;
for i=2:n
sumce=sumce+(y(i)-yn(i));
end
ce=sumce/(n-1);
sum2=0;
for i=2:n;
sum2=sum2+(y(i)-yn(i)-ce).^2;
end
s2=sqrt(sum2/(n-1));
c=(s2)/(s1);
disp(['后验差比值为:',num2str(c)]);
if c<0.35
disp('系统预测精度好')
else if c<0.5
disp('系统预测精度合格')
else if c<0.65
disp('系统预测精度勉强')
else
disp('系统预测精度不合格')
end
end
end
disp(['下个拟合值为 ',num2str(ys(n+1))]);
disp(['再下个拟合值为',num2str(ys(n+2))]);
直接输入一个矩阵,如:[1,2,3,4,5,6]
程序直接输入一个拟合好的图,还有下一个和再下一个的拟合值
四、dijkstra
这个相信大家都比较熟悉,就是一个求起点与终点距离最近的算法
原理也不说了,直接上代码:
tulun1.m
weight= [0 2 8 1 Inf Inf Inf Inf Inf Inf Inf;
2 0 6 Inf 1 Inf Inf Inf Inf Inf Inf;
8 6 0 7 5 1 2 Inf Inf Inf Inf;
1 Inf 7 0 Inf Inf 9 Inf Inf Inf Inf;
Inf 1 5 Inf 0 3 Inf 2 9 Inf Inf;
Inf Inf 1 Inf 3 0 4 Inf 6 Inf Inf;
Inf Inf 2 9 Inf 4 0 Inf 3 1 Inf;
Inf Inf Inf Inf 2 Inf Inf 0 7 Inf 9;
Inf Inf Inf Inf 9 6 3 7 0 1 2;
Inf Inf Inf Inf Inf Inf 1 Inf 1 0 4;
Inf Inf Inf Inf Inf Inf Inf 9 2 4 0;];
[dis, path]=dijkstra(weight,1, 11)
dijkstra.m
function [min,path]=dijkstra(w,start,terminal)
n=size(w,1); label(start)=0; f(start)=start;
for i=1:n
if i~=start
label(i)=inf;
end, end
s(1)=start; u=start;
while length(s)<n
for i=1:n
ins=0;
for j=1:length(s)
if i==s(j)
ins=1;
end,
end
if ins==0
v=i;
if label(v)>(label(u)+w(u,v))
label(v)=(label(u)+w(u,v));
f(v)=u;
end,
end,
end
v1=0;
k=inf;
for i=1:n
ins=0;
for j=1:length(s)
if i==s(j)
ins=1;
end,
end
if ins==0
v=i;
if k>label(v)
k=label(v); v1=v;
end,
end,
end
s(length(s)+1)=v1;
u=v1;
end
min=label(terminal); path(1)=terminal;
i=1;
while path(i)~=start
path(i+1)=f(path(i));
i=i+1 ;
end
path(i)=start;
L=length(path);
path=path(L:-1:1);
注意几个不同的代码块要写在不同的脚本中
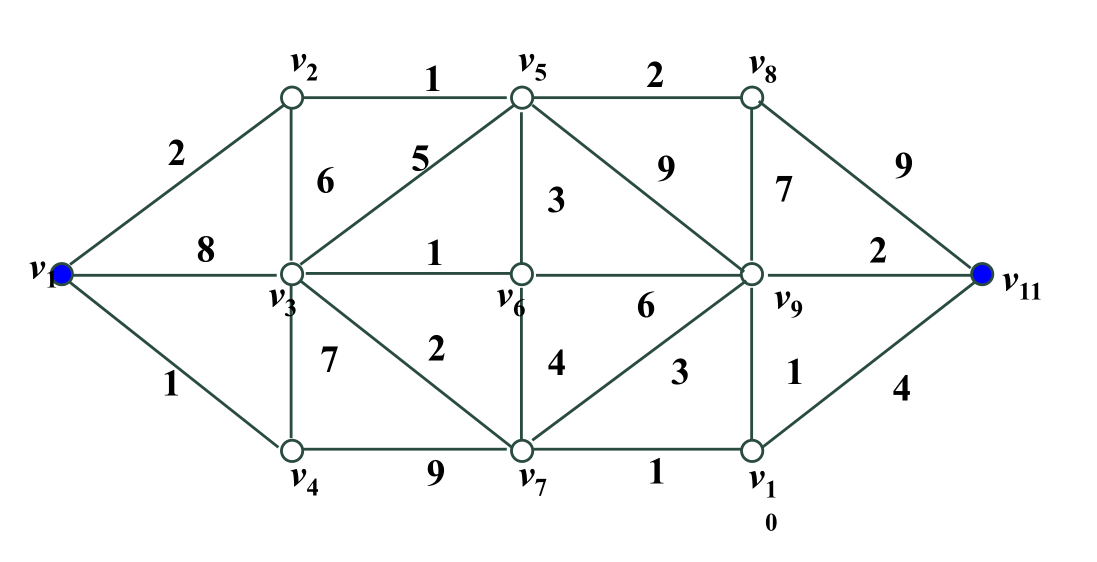
输入时直接输入矩阵:
D=
[0 2 8 1 Inf Inf Inf Inf Inf Inf Inf;
2 0 6 Inf 1 Inf Inf Inf Inf Inf Inf;
8 6 0 7 5 1 2 Inf Inf Inf Inf;
1 Inf 7 0 Inf Inf 9 Inf Inf Inf Inf;
Inf 1 5 Inf 0 3 Inf 2 9 Inf Inf;
Inf Inf 1 Inf 3 0 4 Inf 6 Inf Inf;
Inf Inf 2 9 Inf 4 0 Inf 3 1 Inf;
Inf Inf Inf Inf 2 Inf Inf 0 7 Inf 9;
Inf Inf Inf Inf 9 6 3 7 0 1 2;
Inf Inf Inf Inf Inf Inf 1 Inf 1 0 4;
Inf Inf Inf Inf Inf Inf Inf 9 2 4 0;]
Dij不等于Inf时,Dij里面的值就是i到j的距离
五、模拟退火算法
求TSP问题:
旅行商问题,即TSP 问题(Travelling SalesmanProblem )又译为旅行推销员问题、货郎担问题,是数学领域中著名问题之一。假设有一个旅行商人要拜访n 个城市,他必须选择所要走的路径,路径的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。迄今为止,这类问题中没有一个找到有效算法。倾向于接受NP 完全问题(NP-Complet 或NPC )和NP 难题(NP-Hard 或NPH )不存在有效算法这一猜想,认为这类问题的大型实例不能用精确算法求解,必须寻求这类问题的有效的近似算法。
直接上代码:
swap.m
function [ newpath , position ] = swap( oldpath , number )
% 对 oldpath 进 行 互 换 操 作
% number 为 产 生 的 新 路 径 的 个 数
% position 为 对 应 newpath 互 换 的 位 置
m = length( oldpath ) ; % 城 市 的 个 数
newpath = zeros( number , m ) ;
position = sort( randi( m , number , 2 ) , 2 ); % 随 机 产 生 交 换 的 位 置
for i = 1 : number
newpath( i , : ) = oldpath ;
% 交 换 路 径 中 选 中 的 城 市
newpath( i , position( i , 1 ) ) = oldpath( position( i , 2 ) ) ;
newpath( i , position( i , 2 ) ) = oldpath( position( i , 1 ) ) ;
end
pathfare.m
function [ objval ] = pathfare( fare , path )
% 计 算 路 径 path 的 代 价 objval
% path 为 1 到 n 的 排 列 ,代 表 城 市 的 访 问 顺 序 ;
% fare 为 代 价 矩 阵 , 且 为 方 阵 。
[ m , n ] = size( path ) ;
objval = zeros( 1 , m ) ;
for i = 1 : m
for j = 2 : n
objval( i ) = objval( i ) + fare( path( i , j - 1 ) , path( i , j ) ) ;
end
objval( i ) = objval( i ) + fare( path( i , n ) , path( i , 1 ) ) ;
end
distance.m
function [ fare ] = distance( coord )
% 根 据 各 城 市 的 距 离 坐 标 求 相 互 之 间 的 距 离
% fare 为 各 城 市 的 距 离 , coord 为 各 城 市 的 坐 标
[ v , m ] = size( coord ) ; % m 为 城 市 的 个 数
fare = zeros( m ) ;
for i = 1 : m % 外 层 为 行
for j = i : m % 内 层 为 列
fare( i , j ) = ( sum( ( coord( : , i ) - coord( : , j ) ) .^ 2 ) ) ^ 0.5 ;
fare( j , i ) = fare( i , j ) ; % 距 离 矩 阵 对 称
end
end
myplot.m
function [ ] = myplot( path , coord , pathfar )
% 做 出 路 径 的 图 形
% path 为 要 做 图 的 路 径 ,coord 为 各 个 城 市 的 坐 标
% pathfar 为 路 径 path 对 应 的 费 用
len = length( path ) ;
clf ;
hold on ;
title( [ '近似最短路径如下,路程为' , num2str( pathfar ) ] ) ;
plot( coord( 1 , : ) , coord( 2 , : ) , 'ok');
pause( 0.4 ) ;
for ii = 2 : len
plot( coord( 1 , path( [ ii - 1 , ii ] ) ) , coord( 2 , path( [ ii - 1 , ii ] ) ) , '-b');
x = sum( coord( 1 , path( [ ii - 1 , ii ] ) ) ) / 2 ;
y = sum( coord( 2 , path( [ ii - 1 , ii ] ) ) ) / 2 ;
text( x , y , [ '(' , num2str( ii - 1 ) , ')' ] ) ;
pause( 0.4 ) ;
end
plot( coord( 1 , path( [ 1 , len ] ) ) , coord( 2 , path( [ 1 , len ] ) ) , '-b' ) ;
x = sum( coord( 1 , path( [ 1 , len ] ) ) ) / 2 ;
y = sum( coord( 2 , path( [ 1 , len ] ) ) ) / 2 ;
text( x , y , [ '(' , num2str( len ) , ')' ] ) ;
pause( 0.4 ) ;
hold off ;
clear;
% 程 序 参 数 设 定
Coord = ... % 城 市 的 坐 标 Coordinates
[ 0.6683 0.6195 0.4 0.2439 0.1707 0.2293 0.5171 0.8732 0.6878 0.8488 ; ...
0.2536 0.2634 0.4439 0.1463 0.2293 0.761 0.9414 0.6536 0.5219 0.3609 ] ;
t0 = 1 ; % 初 温 t0
iLk = 20 ; % 内 循 环 最 大 迭 代 次 数 iLk
oLk = 50 ; % 外 循 环 最 大 迭 代 次 数 oLk
lam = 0.95 ; % λ lambda
istd = 0.001 ; % 若 内 循 环 函 数 值 方 差 小 于 istd 则 停 止
ostd = 0.001 ; % 若 外 循 环 函 数 值 方 差 小 于 ostd 则 停 止
ilen = 5 ; % 内 循 环 保 存 的 目 标 函 数 值 个 数
olen = 5 ; % 外 循 环 保 存 的 目 标 函 数 值 个 数
% 程 序 主 体
m = length( Coord ) ; % 城 市 的 个 数 m
fare = distance( Coord ) ; % 路 径 费 用 fare
path = 1 : m ; % 初 始 路 径 path
pathfar = pathfare( fare , path ) ; % 路 径 费 用 path fare
ores = zeros( 1 , olen ) ; % 外 循 环 保 存 的 目 标 函 数 值
e0 = pathfar ; % 能 量 初 值 e0
t = t0 ; % 温 度 t
for out = 1 : oLk % 外 循 环 模 拟 退 火 过 程
ires = zeros( 1 , ilen ) ; % 内 循 环 保 存 的 目 标 函 数 值
for in = 1 : iLk % 内 循 环 模 拟 热 平 衡 过 程
[ newpath , v ] = swap( path , 1 ) ; % 产 生 新 状 态
e1 = pathfare( fare , newpath ) ; % 新 状 态 能 量
% Metropolis 抽 样 稳 定 准 则
r = min( 1 , exp( - ( e1 - e0 ) / t ) ) ;
if rand < r
path = newpath ; % 更 新 最 佳 状 态
e0 = e1 ;
end
ires = [ ires( 2 : end ) e0 ] ; % 保 存 新 状 态 能 量
% 内 循 环 终 止 准 则 :连 续 ilen 个 状 态 能 量 波 动 小 于 istd
if std( ires , 1 ) < istd
break ;
end
end
ores = [ ores( 2 : end ) e0 ] ; % 保 存 新 状 态 能 量
% 外 循 环 终 止 准 则 :连 续 olen 个 状 态 能 量 波 动 小 于 ostd
if std( ores , 1 ) < ostd
break ;
end
t = lam * t ;
end
pathfar = e0 ;
% 输 入 结 果
fprintf( '近似最优路径为:\n ' )
%disp( char( [ path , path(1) ] + 64 ) ) ;
disp(path)
fprintf( '近似最优路径路程\tpathfare=' ) ;
disp( pathfar ) ;
myplot( path , Coord , pathfar ) ;
输入数据的时候注意:
要输入两行,每行之间;分开,上面一行表示每个点的x坐标,下面一行表示每个点的y坐标
如:[ 66.83 61.95 40 24.39 17.07 22.93 51.71 87.32 68.78 84.88 50 40 25 ;
25.36 26.34 44.39 14.63 22.93 76.1 94.14 65.36 52.19 36.09 30 20 26] ;
程序输出走的路线和总路程
如:
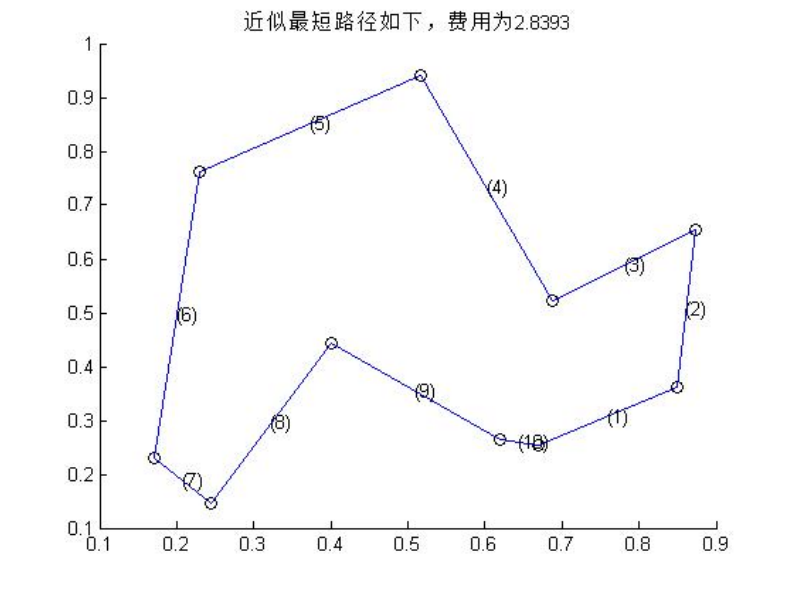
六、种群竞争模型
求两个不同的群体共同生存时,两个群体的增长(下降)趋势
代码:
fun.m:
function dx=fun(t,x,r1,r2,n1,n2,s1,s2)
r1=1;
r2=1;
n1=100;
n2=100;
s1=0.5;
s2=2;
dx=[r1*x(1)*(1-x(1)/n1-s1*x(2)/n2);r2*x(2)*(1-s2*x(1)/n1-x(2)/n2)];
p3.m:
h=0.1;%所取时间点间隔
ts=[0:h:30];%时间区间
x0=[10,10];%初始条件
opt=odeset('reltol',1e-6,'abstol',1e-9);%相对误差1e-6,绝对误差1e-9
[t,x]=ode45(@fun,ts,x0,opt);%使用5级4阶龙格—库塔公式计算
plot(t,x(:,1),'r',t,x(:,2),'b','LineWidth',2),grid;
pause;
plot(x(:,1),x(:,2),'LineWidth',2),grid %作相轨线
我们运行程序的时候主要改动r1,r2,n1,n2,s1,s2,具体含义看下面

七、线性规划模型
求多元一次方程的最优解
如:

那么,其Lingo程序为:
max=2*x1+3*x2;
x1+2*x2<=8;
4*x1<=16;
4*x2<=12;
类似的可以通过变换程序中的数据来求解你的问题
八、非线性与0/1问题
非线性:
如:

这样的问题可以用Lingo解决:
max=98*x1+277*x2-x1*x1-0.3*x1*x2-2*x2*x2;
x1+x2<100;
x1<=2*x2;
类似的可以通过变换程序中的数据来求解你的问题
0/1问题:
01 规划是指未知量的取值范围只能是0,1 的规划问题,通常是线性规划
如:


那么这样可以用Lingo程序解决:
Min=8*x11+13*x12+18*x13+23*x14+10*x21+14*x22+16*x23+27*x24+2*x31+10*x32+21*x33+26*x34+14*x41+22*x42+26*x43+28*x44;
x11+x12+x13+x14=1;
x21+x22+x23+x24=1;
x31+x32+x33+x34=1;
x41+x42+x43+x44=1;
x11+x21+x31+x41=1;
x12+x22+x32+x42=1;
x13+x23+x33+x43=1;
x14+x24+x34+x44=1;
end
int16
类似的可以通过变换程序中的数据来求解你的问题
九、主成分分析
提取决定总目标的某几个最主要的成分
如:求以下决定地区排名的2个最主要的成分
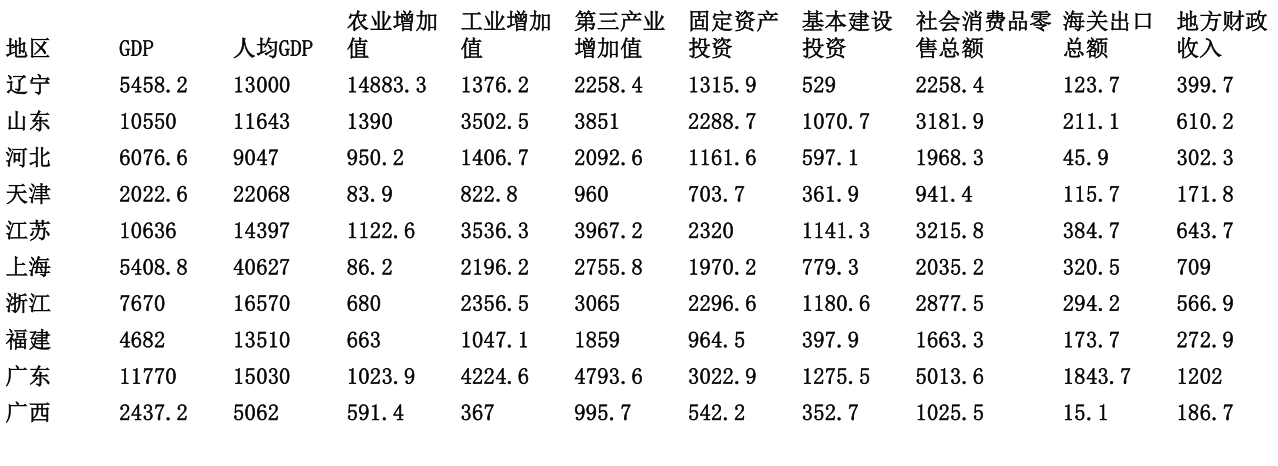
具体使用方法:https://wenku.baidu.com/view/694c8459effdc8d376eeaeaad1f34693daef1087.html
十、聚类分析
将一堆分散的点分成分成几大类
主要用途:将坐标上的分散点按照远近分成几类
python代码:
import numpy as np
import matplotlib.pyplot as plt
# 两点距离
def distance(e1, e2):
# e1:[x1,y1] e2:[x2,y2]
# |e1,e2|=((x1-x2)^2+(y1-y2)^2)^(1/2)
return np.sqrt((e1[0]-e2[0])**2+(e1[1]-e2[1])**2)
# 集合中心
def means(arr):
# 求 [所有点x的平均值 , 所有点y的平均值]
return np.array([np.mean([e[0] for e in arr]), np.mean([e[1] for e in arr])])
# arr中距离a最远的元素,用于初始化聚类中心
def farthest(k_arr, arr):
f = [0, 0]
max_d = 0
for e in arr:
d = 0
for i in range(len(k_arr)):
d = d + np.sqrt(distance(k_arr[i], e))
if d > max_d:
max_d = d
f = e
return f
# arr中距离a最近的元素,用于聚类
def closest(a, arr):
c = arr[1]
min_d = distance(a, arr[1])
arr = arr[1:]
for e in arr:
d = distance(a, e)
if d < min_d:
min_d = d
c = e
return c # 返回[x,y]
if __name__=="__main__":
## 生成二维随机坐标,手上有数据集的朋友注意,理解arr改起来就很容易了
## arr是一个数组,每个元素都是一个二元组,代表着一个坐标
## arr形如:[ (x1, y1), (x2, y2), (x3, y3) ... ]
arr = np.random.randint(100, size=(100, 1, 2))[:, 0, :] # arr是随机二维点集
'''
arr =
[[75 57]
[24 51]
[59 63]
[62 75]
[78 98]
.
.
.
[77 45]
[95 53]
[73 41]
[96 19]
[19 29]
[62 35]
[79 85]]
'''
## 初始化聚类中心和聚类容器
m = 5 # 中心点个数
# 随机选取一个数a作为中心点
a = np.random.randint(len(arr) - 1)
k_arr = np.array([arr[a]])
cla_arr = [[]]
for i in range(m-1):
k = farthest(k_arr, arr) # 求与中心点集最远的点
# k:[x,y]
k_arr = np.concatenate([k_arr, np.array([k])]) # concatenate 实现矩阵拼接(更新中心点集)
cla_arr.append([])
# k_arr 中包含的元素即中心点的集合
## 迭代聚类
n = 20
cla_temp = cla_arr
for i in range(n): # 迭代n次
for e in arr: # 把集合里每一个元素聚到最近的类
ki = 0 # 假定距离第一个中心最近
min_d = distance(e, k_arr[ki])
for j in range(1, len(k_arr)):
if distance(e, k_arr[j]) < min_d: # 找到更近的聚类中心
min_d = distance(e, k_arr[j])
ki = j
cla_temp[ki].append(e) # 距离e最近的中心点的集合中加入e
# 迭代更新聚类中心
for k in range(len(k_arr)):
if n - 1 == i:
break
k_arr[k] = means(cla_temp[k]) # 每迭代一次,就更新中心点为距离自己最近的点的平均值,即将距离较近的一堆点压缩成一个点
cla_temp[k] = []
## 可视化展示
col = ['HotPink', 'Aqua', 'Chartreuse', 'yellow', 'LightSalmon']
for i in range(m):
plt.scatter(k_arr[i][0], k_arr[i][1], linewidth=10, color=col[i])
plt.scatter([e[0] for e in cla_temp[i]], [e[1] for e in cla_temp[i]], color=col[i])
plt.show()
大家运行的时候只需要把程序中的arr改成自己的点阵就可以了
如:arr=[[1,2],
[3,4],
......
]
程序运行出来就是这样:
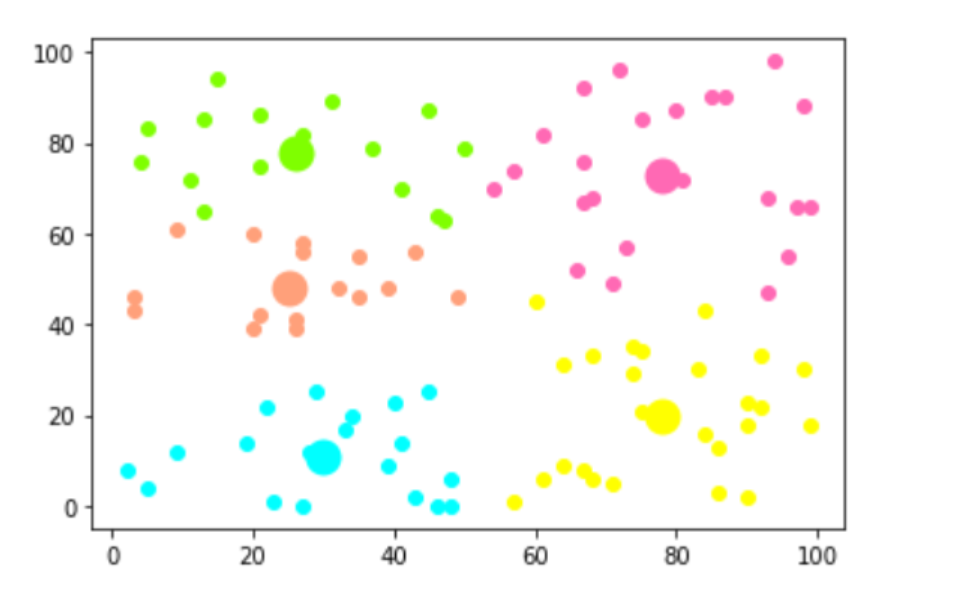
到这里美赛的算法介绍就over了


 浙公网安备 33010602011771号
浙公网安备 33010602011771号