指数与对数
指数与对数在实际应用中有着广泛的应用,例如在统计学中,指数函数可以用来描述一个现象的变化速度,对数函数可以用来描述一个现象的变化幅度。此外,指数与对数也是数学中的基本概念,在解析几何、微积分等数学分支中都有着重要的应用。
指数函数(Exponential Function)是一种自变量为实数的函数,其函数值随着自变量的增加而成指数级数增加,指数级的增加幅度更高;


对数函数(Logarithmic Function)则是一种自变量为实数的函数,其函数值随着自变量的增加而成对数级数增加,对数级增加的幅度更低。



指数:
指数函数的概念:

要点诠释:
(1)形式上的严格性:

(2)为什么规定底数a大于零且不等于1:

要点2:指数函数的图象及性质
象限(Quadrant),是平面直角坐标系(笛卡尔坐标系)中里的横轴和纵轴所划分的四个区域,每一个区域叫做一个象限。主要应用于三角学和复数中的坐标系。象限以原点为中心,x,y轴为分界线。右上的称为第一象限,左上的称为第二象限,左下的称为第三象限,右下的称为第四象限。原点 [3] 和坐标轴上的点不属于任何象限。

要点诠释:

要点3:指数函数底数变化与图像分布规律
(1)
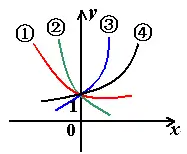

(2)特殊函数
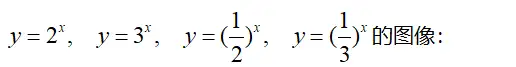
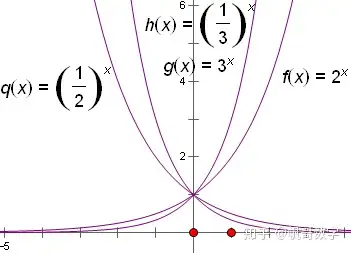
对数:



对数源于指数,是指数函数反函数
因为:y = ax
所以:x = logay
对数的定义
【定义】如果 N=ax(a>0,a≠1),即a的x次方等于N(a>0,且a≠1),那么数x叫做以a为底N的对数(logarithm),记作:
其中,a叫做对数的底数,N叫做真数,x叫做 “以a为底N的对数”。
对数的表示及性质:
对数的本质是对求幂的逆运算。 这意味着一个数字的对数是必须产生另一个固定数字(基数)的指数。
1.以a为底N的对数记作:logaN
2.以10为底的常用对数:lgN = log10N
3.以无理数e(e=2.71828...)为底的自然对数记作:lnN = logeN
4.零没有对数.
5.在实数范围内,负数无对数。 [3]在虚数范围内,负数是有对数的。
参考:
指数对数幂函数,基础有问题就看这篇! - 知乎 (zhihu.com)



【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 微软正式发布.NET 10 Preview 1:开启下一代开发框架新篇章
· 没有源码,如何修改代码逻辑?
· DeepSeek R1 简明指南:架构、训练、本地部署及硬件要求
· NetPad:一个.NET开源、跨平台的C#编辑器
· 面试官:你是如何进行SQL调优的?