并查集算法
并查集算法
描述
对于给定的点,和点连接成的边,判断是否存在环。比如下图是存在。
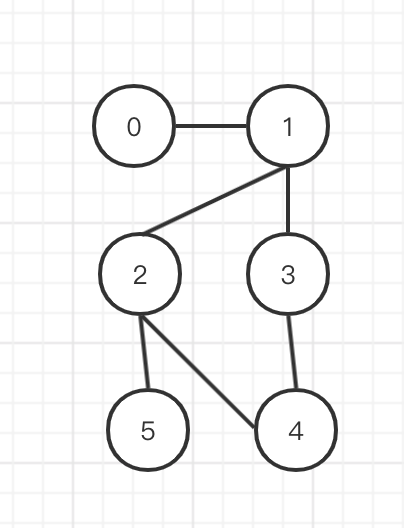
推导
- 如果给定了边(0,1),(2,3),(3,4),(1,2),将这些点加入到一个set中[0,1,2,3,4],则在这个集合中任意取非边两点都会形成一个环。
如图,如果有任意边(0,1),(3,4),(2,1),可以得到以下图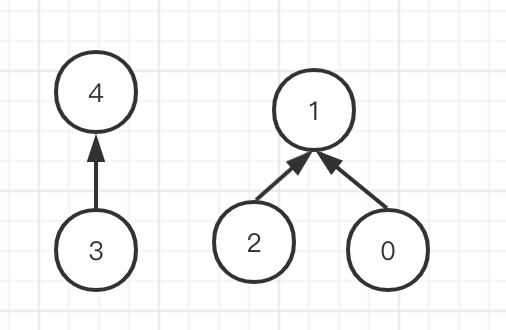
又给定边(3,1)这条边的两个节点位于已知图上,如果直接用3连到1,会使一个节点有两个父节点,出现了断层,即无法判断层级关系,如果用1连到3,会使路径过长。正确的做法应该用他们的父节点相连。不考虑压缩路径的情况下,1连4或4连一都可以。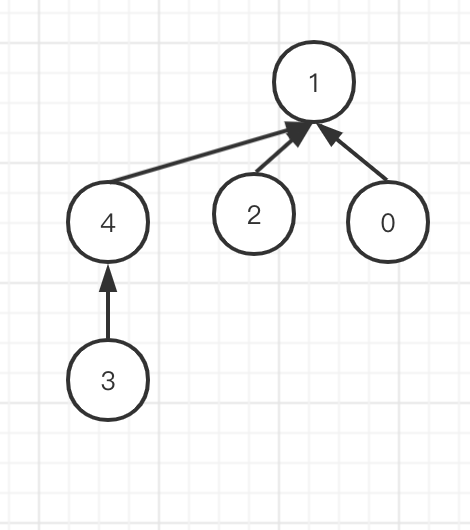
思考:为什么要连3,1?
- 将它和集合联系起来,java中set是用树来实现的,集合必定有且只有一个根节点,如果是根据形成环的定理来判断,要将这些点都要归为一个树结构。
这样若给定边如(2,4),他们的跟节点都是1,所以是集合内的,必定会形成环。给定(2,5),无公共根节点,所以不会形成环,但是如果再给定(5,4),根节点都是1,会形成环。
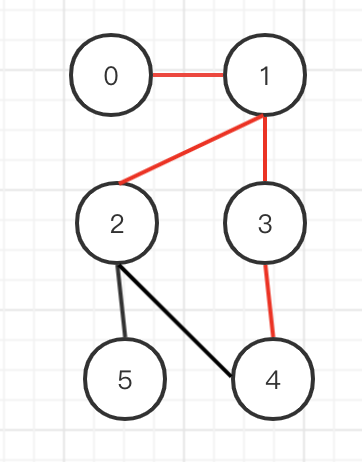
代码实现
设定一个列表,列表的索引表示当前节点,索引对应的值代表父节点。
-
为什么要压缩路径
union_func方法中,如果直接parent[x_root] = y_root,最差情况会按链表的顺序来合并,比如,(0,1),(1,2),,,(999,1000),这样会有1000层查找即空间复杂度为On。压缩路径的话,如果是顺序节点的话,不会向下发展数的高度,只会多生长叶子结点,使得时间复杂度为O1。
# 顶点数
vertices = 6
# 所有点设为-1
parent = [-1] * vertices
# rank代表层级
rank = [0] * vertices
# 寻找根节点:列表中的元素值是父节点的索引
def find_root(x: int, li: list):
x_root = x
while li[x_root] != -1:
x_root = li[x_root]
return x_root
# 合并 返回1合并成功 返回0合并失败
def union_func(x: int, y: int, li: list, rank: list):
x_root = find_root(x, li)
y_root = find_root(y, li)
if x_root == y_root:
return 0
else:
# parent[x_root] = y_root
# 压缩路径
if rank[x_root] > rank[y_root]:
parent[y_root] = x_root
elif rank[y_root] > rank[x_root]:
parent[x_root] = y_root
else:
parent[y_root] = x_root
rank[x_root] += 1
return 1
def main():
edges = [
[0, 1], [1, 2], [1, 3],
[2, 4], [3, 4], [2, 5]
]
for i in range(len(edges)):
x = edges[i][0]
y = edges[i][1]
if union_func(x, y, parent,rank) == 0:
print("cycle detected")
return
print("no cycle")
return
if __name__ == '__main__':
main()

