JavaScript中弧度和角度的转换

弧度 = 角度 * Math.PI / 180
角度 = 弧度 * 180 / Math.PI

在JavaScript Math 对象中:

sin() 方法可返回一个数字的正弦。
tan() 方法可返回一个表示某个角的正切的数字。

Math.sin(x)
Math.tan(x)

参数x是必需。一个以弧度表示的角。将角度乘以 0.017453293 （2PI / 360）即可转换为弧度（即 角度 * Math.PI / 180）。

---

cos() 方法可返回一个数字的余弦值。

Math.cos(x)

参数x是必需。必须是一个数值。

---

asin() 方法可返回一个数的反正弦值。
acos() 方法可返回一个数的反余弦。

Math.asin(x)
Math.acos(x)

参数x是必需。必须是一个数值，该值介于 x∈[-1, 1]。

---

atan() 方法可返回数字的反正切值。

Math.atan(x)

参数x是必需。必须是一个数值。

---

pow() 方法可返回 x 的 y 次幂的值。

Math.pow(x,y)

参数x是必需。底数。必须是数字。
参数y是必需。幂数。必须是数字。

---

sqrt() 方法可返回一个数的平方根。

Math.sqrt(x)

参数x必需。必须是大于等于 0 的数。

---

• 复习三角函数

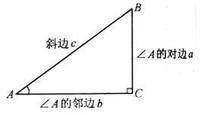
正弦(sin)：对边比斜边 sinA = a / c

余弦(cos)：邻边比斜边 cosA = b / c

正切(tan)：对边比邻边 tanA = a / b

余切(cot)：邻边比对边 cotA = b / a

正割(sec)：斜边比邻边

余割(csc)：斜边比对边

• 正弦定理

sinA / a = sinB / b = sinC / c

也可表示为:

a / sinA = b / sinB = c / sinC = 2R(R是三角形的外接圆半径)

三角函数正弦定理可用于求得三角形的面积:

S = 1/2absinC = 1/2bcsinA = 1/2acsinB

• 余弦定理

a² = b² + c² - 2bc · cosA
b² = a² + c² - 2ac · cosB
c² = a² + b² - 2ab · cosC

也可表示为:

cosA=（c² +b² -a²）/ 2bc
cosB=（a² +c² -b²）/ 2ac
cosC=（a² +b² －c²）/ 2ab

第一余弦定理:

a = b·cosC + c·cosB
b = c·cosA + a·cosC
c = a·cosB + b·cosA

• 正切定理

(a + b) / (a - b) = tan((A + B) / 2) / tan((A - B) / 2)