梯度下降法
梯度下降法主要分为三种,
- 梯度下降法
- 随机梯度下降
- 小批量梯度下降
下面分别来介绍一下,这样更加有助于理解它们之间的联系。
梯度下降法
梯度下降使用整个训练数据集来计算梯度,因此它有时也被称为批量梯度下降
下面就以均方误差讲解一下,假设损失函数如下:
其中 是预测值,
是真实值,那么要最小化上面损失
,需要对每个参数
运用梯度下降法:
其中 是损失函数对参数
的偏导数、
是学习率,也是每一步更新的步长。
随机梯度下降法
在机器学习\深度学习中,目标函数的损失函数通常取各个样本损失函数的平均,那么假设目标函数为:
其中 是第
个样本的目标函数,那么目标函数在在
处的梯度为:
如果使用梯度下降法(批量梯度下降法),那么每次迭代过程中都要对 个样本进行求梯度,所以开销非常大,随机梯度下降的思想就是随机采样一个样本
来更新参数,那么计算开销就从
下降到
。
小批量梯度下降法
随机梯度下降虽然提高了计算效率,降低了计算开销,但是由于每次迭代只随机选择一个样本,因此随机性比较大,所以下降过程中非常曲折(图片来自《动手学深度学习》),
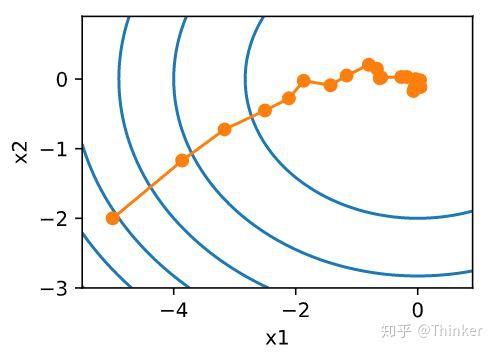
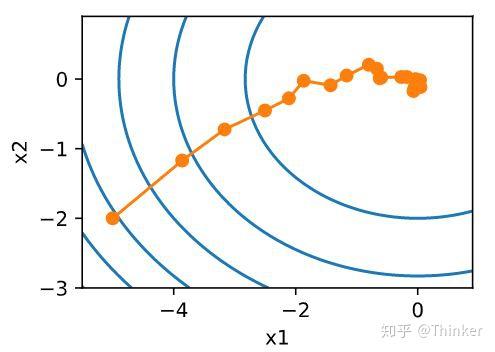
所以,样本的随机性会带来很多噪声,我们可以选取一定数目的样本组成一个小批量样本,然后用这个小批量更新梯度,这样不仅可以减少计算成本,还可以提高算法稳定性。小批量梯度下降的开销为 其中
是批量大小。
*该怎么选择?*
当数据量不大的时候可以选择批量梯度下降法,当数据量很大时可以选择小批量梯度下降法。
参考链接:



