MatrixVT：高效View Transformation，让视觉BEV梦想照进现实

原论文：MatrixVT: Efficient Multi-Camera to BEV Transformation for 3D Perception

来自：CVPR2022，旷视科技，Submission-2022.11

针对目前BEV中更有优势的Lift-Splat类方法中关键模块（Vision Transformation），MatrixVT实现了非常优雅的优化，在保持模型性能（甚至略微提高）的同时，能大幅降低计算量和内存消耗。

它可应用于几乎所有Lift-Splat类模型上。

Lift-Splat类方法长期占据nuScenes Camera-only Detection Task的Top-5，如BEVDepth、BEVDet等，足以说明此类方法的优越性。

如果您想进一步了解Lift-Splat类模型的核心Lift-Splat原理，可阅读本文作者另一篇论文解读文章《一文读懂BEV自底向上方法：LSS 和 BEVDepth》。

传送门：

一文读懂BEV自底向上方法：LSS 和 BEVDepth

另外，您想了解BEV另一个基于学习的VT方法，例如BEVFormer，可阅读本文作者的论文解读文章《一文读懂BEVFormer论文》和《一文读懂BEVFormer v2: nuScenes camera-only大幅领先的新SOTA》

传送门：

一文读懂BEVFormer论文

一文读懂BEVFormer v2: nuScenes camera-only大幅领先的新SOTA

Motivation

在BEV模型中，Vision Transformation（VT）是把multi-camera 特征转换为BEV特征的关键模块。

现有的VT方法可被划分为2类：

• 基于视觉几何的方法，根据相机投影和深度估计来进行几何转换，例如LSS、BEVDepth；
• 基于学习的方法，让模型学习BEV中某个grid关注相机图像的哪个/哪些位置，例如BEVFormer。

这两类方法中，前者因为用到了几何约束而表现出了更优越的（检测）性能。Lift-Splat是这类方法的典型代表。虽然Lift-splat-like类方法在性能方面的有效性毋庸置疑，但是它有两个问题：

问题一：Splat操作不是普遍常用操作方法

Splat操作的实现要么依赖于非常低效的cumsum trick，要么依赖于只能在特定设备上运行的定制化操作，这都会增加应用BEV感知的成本。

问题二：Lift过程产生的multi-view image features太大

导致multi-view image features成为了BEV模型的memory瓶颈。

这两个问题，在BEV模型训练和inference时都会存在，严重阻碍了BEV方法在自动驾驶中的应用。

MatrixVT就是致力于解决这两个问题。

方法综述

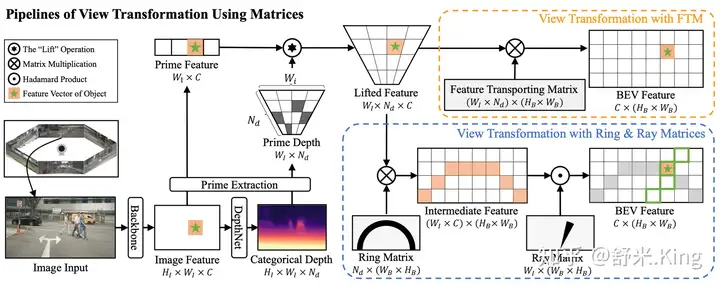
VT是不同视角feature转换的过程，即把lifted multi-view image features和转换矩阵进行矩阵乘（MatMul）得到BEV features，这里把上述特征转换矩阵（feature transporting matrix）叫做FTM。这样就可以把VT过程归纳成纯数学计算形式，避免需要特定的操作。 FTM本质上是表示lift操作得到的multi-view image features（

）中每个点到BEV 中每个grid的映射关系。

然而，通过FTM实现VT又会导致VT退化，这是因为lifted feature所在3D空间和BEV feature的BEV grids之间映射关系非常稀疏如图2所示，这会导致FTM（

）的尺寸巨大以及计算效率很低。

图2. VT可以通过标准操作（如矩阵乘法）来实施，因为在Lift-Splat 类方法的转换过程中，Spalt操作可被表示为二元矩阵（每个BEV grid与哪些Lifted image features有映射关系），这个矩阵很大很稀疏。

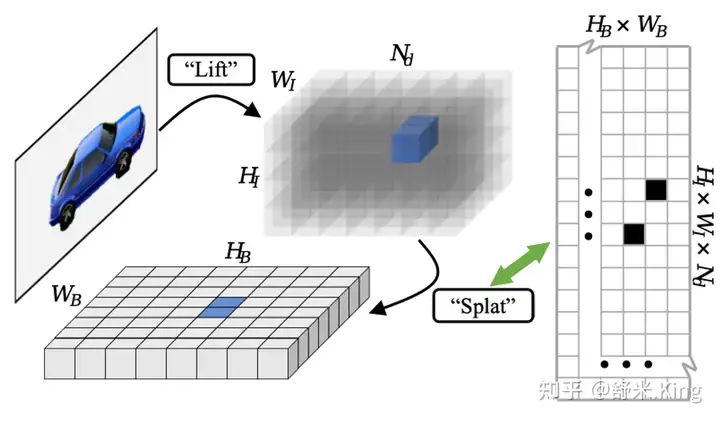
过去的研究，往往都是在寻找一些定制化的操作，其实是回避了稀疏性的本质问题。MatrixVT论文提出了如下两个方法来解决稀疏性映射问题。

• Prime Extraction
  灵感来源于对自动驾驶场景的观察：图像高度方向（即垂直方向）的信息更少，那么就在此维度上把iamge feature压缩。
• 矩阵分解来降低FTM的稀疏性
  通过Ring & Ray 分解法把FTM正交地分解为两个独立的矩阵，分别编码自车为中心极坐标的距离和方向。经过Ring & Ray分解，可以把VT重新编排成数学上等效但更高效的公式。

实施这两个方法如图1下半部分所示，可以数百倍地降低VT的内存占用(memory footprint)和计算，使MatrixVR比现有方法都更高效。

图1. Lift-Splat方法的流程（上），Matrix-VT方法的流程（下）。Matrix方法在VT之前压缩image feature，来减少内存访问量和计算量。Matrix的实现只使用了标准操作，未引入任何特殊操作。

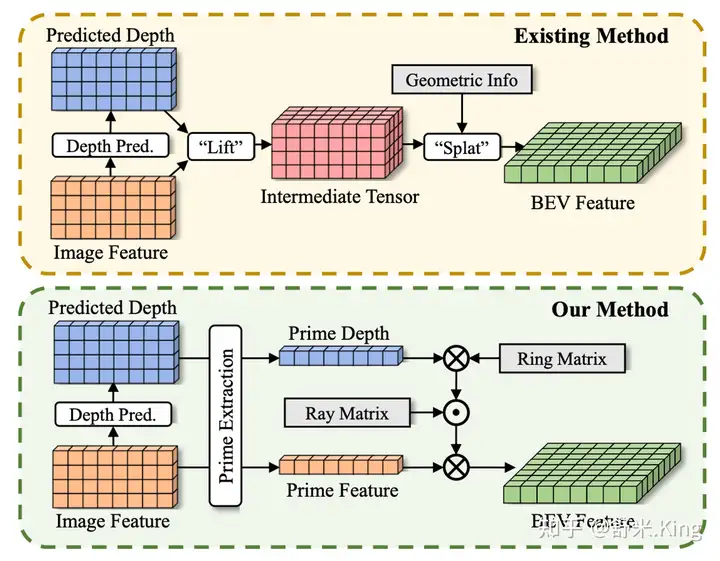
Methods Details

详细讲解MatrixVT创新方法的实现细节。

表1. 本文常用符号定义

Lift-Splat类方法回顾与数学归纳

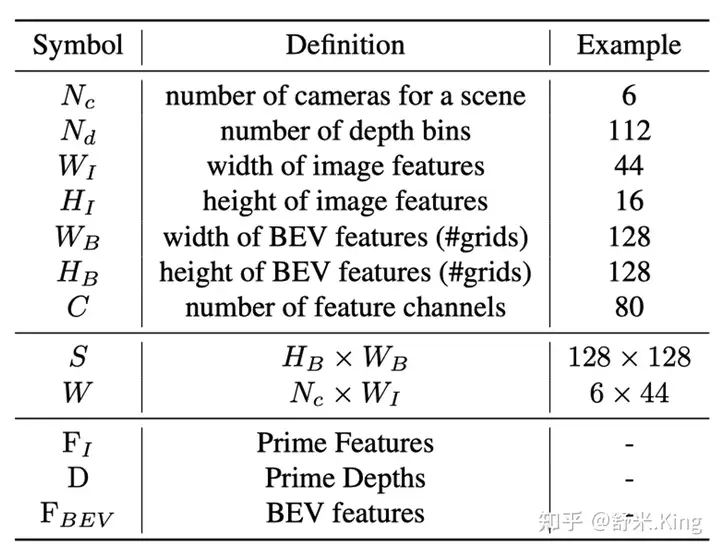
先对论文中涉及的符号进行定义说明：

•  

• 表示相机数目
•  
• 表示Lift时的深度网格数
•  

和

• 分别表示image features的高度和宽度
•  

和

• 分别表示BEV features的高度和宽度
• C表示feature通道数

那么，Lift-Splat过程所涉及输入、输出变量的数学表示如下：

• multi-view image feature可以表示为

• 
  
• Lifted深度估计可以表示为
• 
  
• BEV features可以表示为

• 
  

Lift-Splat VT的第一步（Lift），通过把 F进行逐像地与D进行外积计算，把F ‘lift’到3D空间，得到中间特征Tensor

 

计算过程可以被表示为：

 

 

这个中间特征Tensor可以被看作

个特征向量，每个特征向量都对应物理空间几何坐标系中的一个点。

Lift-Splat VT的第二步（Splat），以往的方法一般采用Pillar Pooling的操作，根据几何坐标把同属于一个BEV Grid的feature向量加到BEV grid中。

本文作者发现，Splat操作本质上是lifted得到的中间特征到BEV grid的固定映射。因此，可以用一个Feature Transporting Matrix来表示这个映射：

 

 

其中

是lifted的中间特征 的矩阵形式， 是BEV特征 的矩阵形式，

是映射矩阵。

把Splat归纳为FTM这种数学形式，消除了定制化操作的要求。

但是，3D空间到BEV grid之间的稀疏映射会让FTM非常巨大且稀疏，导致matrix-based VT非常低效。

下面两个技术（Prime Extraction 和 Ring&Ray分解）可以降低FTM的稀疏性，加速VT过程。

面向自动驾驶的Prime Extraction

图3. 水平和垂直方向的响应强度分析。对自动驾驶而言，水平宽度方向的响应方差比垂直高度方向更高。

高维中间特征

是稀疏映射和低效VT操作的根本原因。直觉上，可以通过减小

尺寸来降低稀疏性，据此作者提出一种面向自动驾驶或类似信息冗余场景的压缩技术——Prime Extraction。

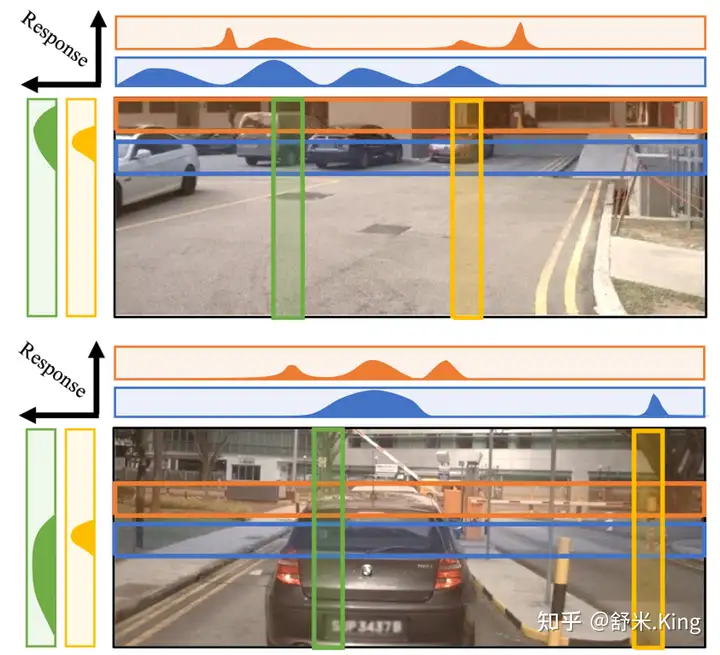
如图3所示，Prime Extraction受针对自动驾驶场景分析的启发：image feature高度方向的响应方差相比于宽度方向更低，这就意味着高度方向的信息量更少。因此作者提出压缩高度方向的image feature。以往的研究工作也曾提出这个方法，但本文首次提出同时在高度方向压缩image feature和相应的深度预测，来加速VT。

Prime Extraction中的Prime就可以直白地理解为响应强度，也可以理解为前景信息/主要信息。

图4. Prime Extraction模块。预估深度在Prime Depth Attention的指导下压缩高度信息；image feature通过PFE进行压缩，包含MaxPooling和一系列卷积层来微调特征。

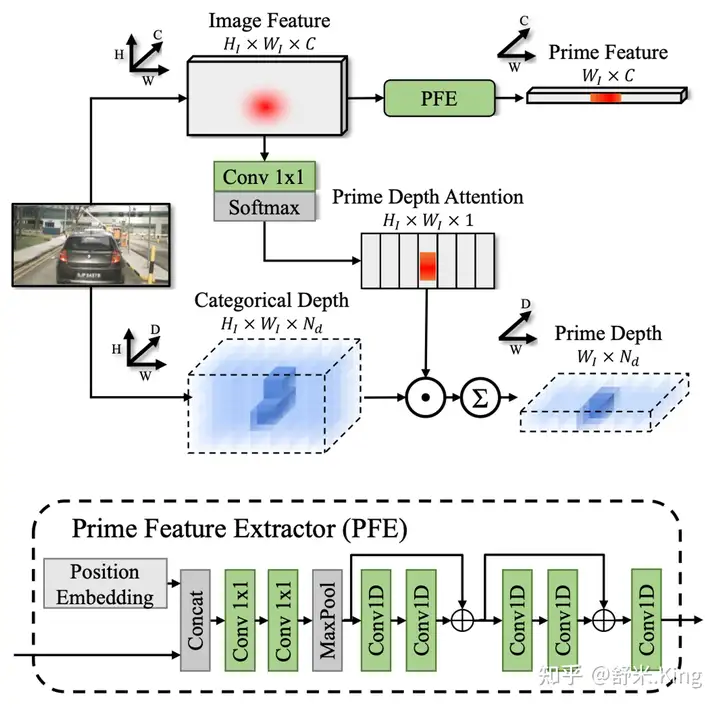
如图4所示，分别说明如何生成Prime Depth和Prime Feature

• Prime Depth
  首先，以multi-view image features作为输入，用卷积和在H方向的Softmax预测出Prime Depth Attention(PDA)。可以把PDA理解为在H方向的深度Attention，即图3中的垂直方向，哪里的响应强度高，哪里的Softmax结果就大。
  然后，对估计深度(Categorical Depth)与PDA进行点积，即每个估计深度点都乘以相应的Prime Depth Attention，得到Intermediate Depth(

)。代码实现时，用Pytorch Tensor的Broadcast机制，把 在 方向广播为 。
最后，再进行H方向的Softmax，得到Prime Depth。Prime Depth中 的一列，就代表W维度某个方向Prime feature（前景特征）的深度估计，实际上是在

• 个深度上的可能性分布。
  代码详见：

class DepthReducer(nn.Module): 	
   ...

• Prime Feature
  以multi-view image features作为输入，经过Position Embedding、Column-wise MaxPool(即H方向求最大值)，然后再进行1-D卷积，得到Prime Feature。这个过程可以理解为，在Height方向对特征进行信息压缩，得到了响应强烈的主要特征。
  代码详见：

class HoriConv(nn.Module): 
   ...

通过Prime Extraction的信息压缩，Prime Depth和Prime Feature都被减小了

倍，同步也把FTM缩小 倍变成了

，利用它们来生成BEV feature的流程如图5所示。

“Ring & Ray” 分解

可以通过矩阵分解，进一步地把稀疏的FTM减小。

图5. VT流程。从图像提取特征并估计每个pixel深度。特征和预估深度被送到Prime Extraction压缩。用压缩后的Prime Feature和Prime Depth，把1维Prime Feature ‘lift’到2D空间（W和Depth维），得到Lifted Feature。然后通过MatMul操作FTM或分解的Ring&Ray matrices，把Lifted Feature转换成BEV feature。

不失一般性地把

设为1， 就变成了

。在极坐标系下：

•  

• 维度可看作方向，因为image feature中每一列相当于一个特定方向的信息。
•  

• 维度可看作距离，因为这个维度就表示深度depth。

换言之，某个特定BEV grid所对应的image feature可通过方向和距离来定位。作者提出把

正交分解为两个矩阵，分别编码方向和距离信息。具体来说就是：

• 用Ray矩阵

• 来编码深度信息；
• 用Ring矩阵

• 来编码距离信息。

上述Ring&Ray分解可以有效地减少静态参数。预定义的参数量从

减少为

，一般会减少30～50倍。

在VT过程中如何使用Ring和Ray矩阵呢？

首先，对Prime Feature和Prime Depth进行与Lift-Splat中一样的逐元素外积计算，得到Lifted feature

：

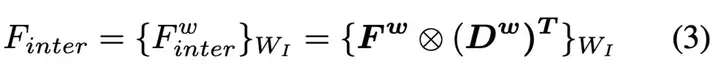
然后，如图5所示，代替黄框中用

直接转换成BEV feature，作者调换了 各个维度的顺序，转换成矩阵 ，然后让Ring矩阵与 进行矩阵相乘得到中间特征(intermediate feature)。然后在把中间特征与Ray矩阵进行哈达玛积，进行编码，然后在

维度相加得到BEV feature，计算过程如下公式：

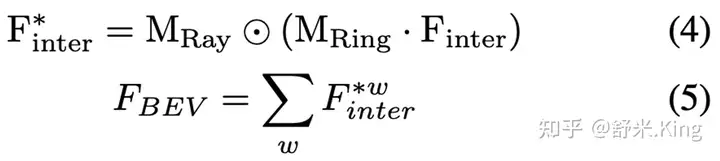
其中，

。

Ring&Ray分解后，按公式3～5逐个计算，没有把VT过程的FLOPs降低，为什么呢，如何解决？

主要是因为在公式3中的Intermediate Feature中就过早地引了feature channel这个维度，同时它也比较大，那么进行4、5计算时都是带着这个feature channel维度来计算的。

为了解决这个问题，作者把上述VT过程涉及的3～5这3个公示联立，变换成数学上相等的形式：

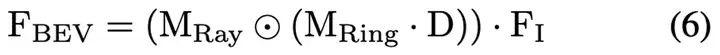
这里

表示Prime Feature，变换后把引入Feature channel的

放在了括号的最外面，即最后一步再计算。那么前两步的矩阵乘积和内积运算就不包含feature channel了。

这样，在常见设置的情况下

，Ring&Ray分解可降低计算量46倍，同时节省96%的内存占用。

VT计算数学变换的说明（Appendix1.2）

论文Appendix1.2给出了公式6的变换证明过程。为了简化，忽略了feature channel的C，这样

就可以写为

。说明一下，这里以及后续的证明公式中，把变量的size标记在了右上角。

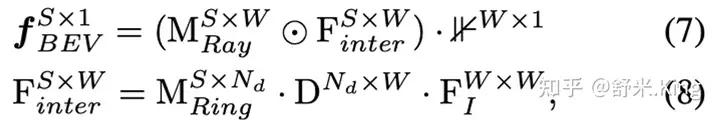
S表示BEV的尺寸，例如128x128的BEV，那么S=128x128=16384；

W表示image feature的宽度；

 

表示深度估计中的离散化深度数目；

 

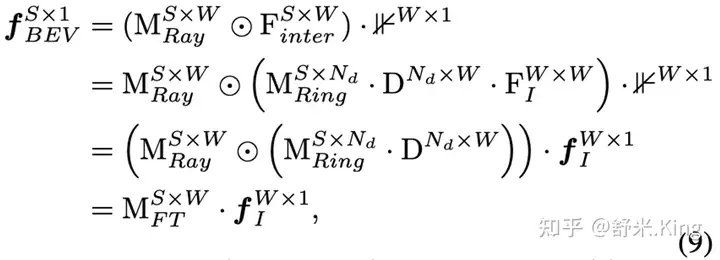
表示Prime Feature 的对角矩阵，这里忽略了feature channel C。公式就第二行中，用对角阵与

相乘，相当于实现了Lift操作的外积计算。

如何生成Ring & Ray 矩阵？

Ring & Ray的生成过程依赖相机的内、外参，它们决定了lifted features与BEV grids的空间几何关系。Ring & Ray矩阵只需要生成一次，这是因为相机位置一般固定不变。

为了简化描述生成Ring & Ray矩阵的算法，这里没有以相机内、外参作为输入，而是采用了lifted Prime Feature的几何位置（2D坐标

），以及BEV Grids （2D grids，坐标为

）。具体算法如下伪代码所示：

大体思路就是：

把Ring & Ray矩阵初始化为0， 遍历

的每个方向和

的每个深度，如果Lifted Feature落在某个grid，就把这个grid所对应的Ring & Ray矩阵的元素置为1。

Experiment

MatrixVT对Lift-Splat类方法中VT部分进行相对独立地优化，因此它可用于改造大多数Lift-Splat类方法，例如论文中MatrixVT的实验都是基于BEVDepth工程进行MatrixVT优化改造。

• 检测性能方面

相比于BEVDepth，MatrixVT的在3D目标检测任务和分割任务的检测性能方面，基本保持不变，甚至某些指标略有提高。

• 计算速度和内存占用方面

MatrixVT在保持模型性能不降的前提下，对提高VT过程的计算速度和减少内存占用量方面，优势非常明显。

另外，在实验中作者还讨论了Prime Extraction的有效性，并可视化地分析了Prime Depth的有效性。

---

相关数学知识回顾

矩阵各种乘法及其代码实现

矩阵乘积（叉乘）

• 定义
  A是m * n矩阵，B是n x p矩阵，C = AB，结果C是m x p的矩阵
• PyTorch用法

a = torch.Tensor([[1,2], [3,4]])
b = torch.Tensor([[5,6], [7,8]])
matrix_product = torch.mm(a, b)
print('matrix_product:', matrix_product)

matrix_product: tensor([[19., 22.],
        [43., 50.]])

Hadamard 积（点乘、内积）

• 定义
  A是m x n矩阵，B也是m x n矩阵，C = A ⊙ B，结果C也是m x n的矩阵
  即对形状相同矩阵中的元素进行逐个对应相乘，产生与输入相同维度的输出矩阵。在数学中，Hadamard乘积（也称为 Schur乘积或逐元素乘积）是一种二元运算。

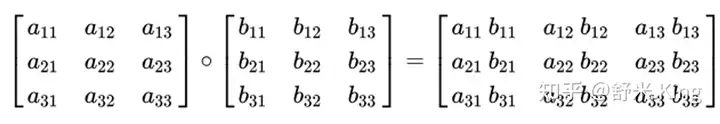
• PyTorch用法

a = torch.Tensor([[1,2], [3,4]])
b = torch.Tensor([[5,6], [7,8]])
hadamard_product = a * b
# hadamard_product = torch.dot(a, b)
print('hadamard_product:', hadamard_product)
 
hadamard_product: tensor([[ 5., 12.],
        [21., 32.]])

Kronecker（外积）

• 定义
  Kronecker 积是两个任意大小矩阵间的运算，表示为 A ⊗ B 。如果 A 是一个 m × n 的矩阵，而 B 是一个 p × q 的矩阵，克罗内克积则是一个 m p × n q 的分块矩阵。克罗内克积也称为直积或张量积。
  即A中任一元素与B中的每个元素相乘，得到p x q的矩阵，然后m x n个A的元素都做相同的操作，得到m x n个p x q的矩阵。

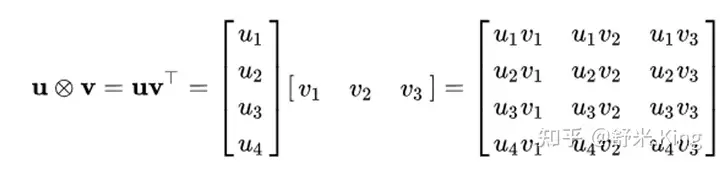
• NumPy用法

import numpy as np
a = np.eye(3)
b = np.ones((3,2,3))
c = np.kron(a,b)