单应性变换与仿射变换
参考链接:单应性变换与仿射变换
一、齐次坐标
(1)从普通坐标转换成齐次坐标时
如果(x,y,z)是个点,则变为(x,y,z,1);
如果(x,y,z)是个向量,则变为(x,y,z,0)
(2)从齐次坐标转换成普通坐标时
如果是(x,y,z,1),则知道它是个点,变成(x,y,z);
如果是(x,y,z,0),则知道它是个向量,仍然变成(x,y,z)
例如:对于一个普通坐标的点P=(Px, Py, Pz),有对应的一族齐次坐标(wPx, wPy, wPz, w),其中w不等于零。比如,P(1, 4, 7)的齐次坐标有(1, 4, 7, 1)、(2, 8, 14, 2)、(-0.1, -0.4, -0.7, -0.1)等等。因此,如果把一个点从普通坐标变成齐次坐标,给x,y,z乘上同一个非零数w,然后增加第4个分量w;如果把一个齐次坐标转换成普通坐标,把前三个坐标同时除以第4个坐标,然后去掉第4个分量。
二、仿射变换
仿射变换是二维坐标到二维坐标之间的线性变换(相同平面)
1、概念
仿射变换包括如下所有变换,以及这些变换任意次序次数的组合:
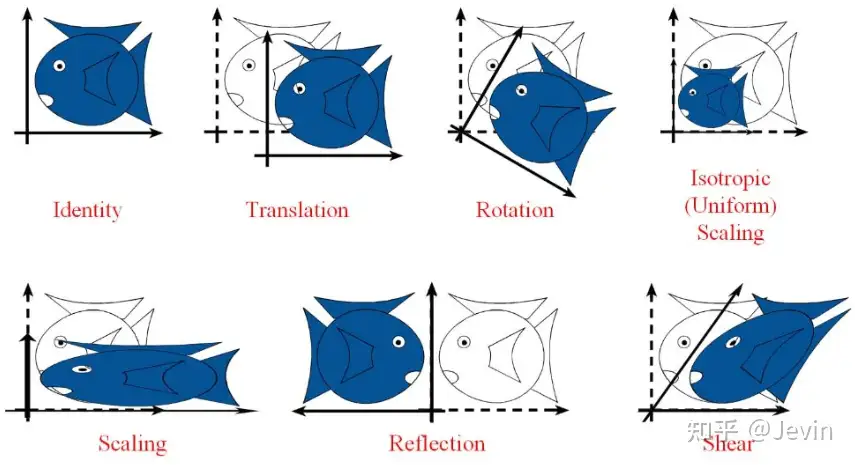
- 平移(translation)和旋转(rotation)的组合称为欧式变换或刚体变换
- 放缩(scaling)可进一步分为uniform scaling和non-uniform scaling,前者每个坐标轴放缩系数相同(各向同性),后者不同;如果放缩系数为负,则会叠加上反射(reflection)
- 刚体变换+uniform scaling称为相似变换,即平移+旋转+各向同性的放缩
- 剪切变换(shear)将所有点沿某一指定方向成比例的平移
- 排除了平移变换的所有仿射变换称为线性变换,有原点位置不变,多次线性变换的结果仍是线性变换
- 实际上仿射变换可以看成基础的线性变换+平移的组合
通常仿射变换对点、线、面具有一定的保持性,这种保持性体现在:
- 经过变换后,点还是点,线还是线,面还是面(如果不是仿射变换而是3D投影的话,在一定的视角下,面有可能变成线,线有可能变成点)
- 经过变换后,平行线和平行面依然平行
- 经过变换后,图形间的某些比例关系保持不变,比如两条平行线的长度比不变,点在线段中的位置比例保持不变
2、仿射变换矩阵
- 平移量为0的仿射变换称为线性变换,可以用下列矩阵表示:

- 只有平移变换而没有线性变换的仿射变换,可以用下列矩阵表示:
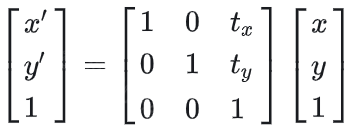
- 将同时含有线性变换和平移变换的仿射变换,用下列矩阵表示:
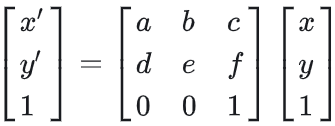
仿射变换的变换矩阵统一用 [������001] 来描述,不同基础变换的a,b,c,d,e,f约束不同,如下所示:
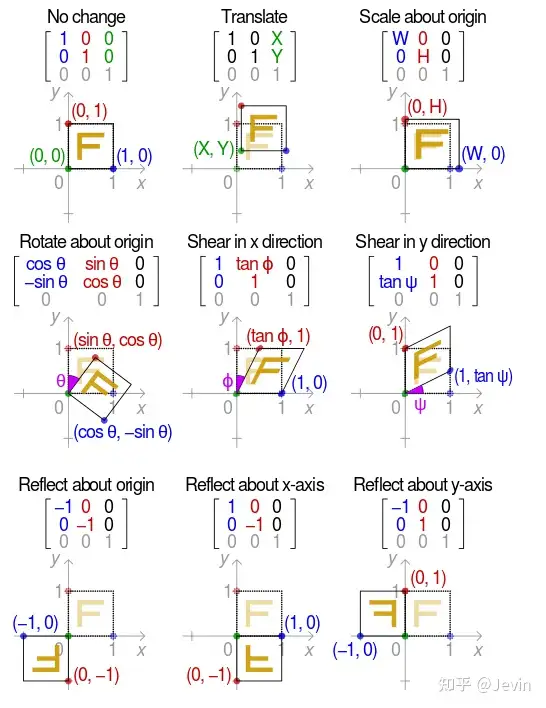
使用三组坐标点,即可求出仿射变换矩阵
3、实验
(1)平移变换
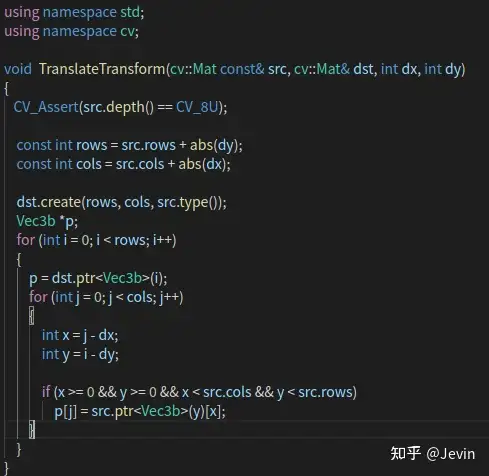
代码:

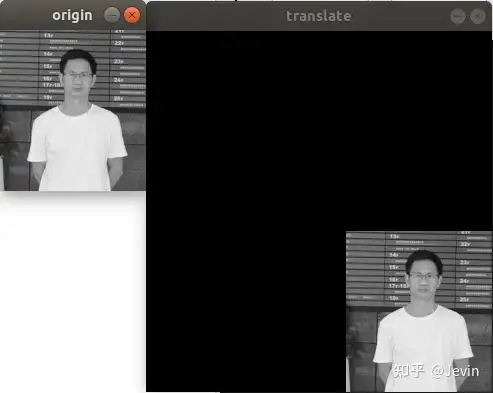
结果:
(2)旋转
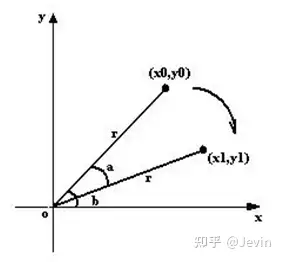
用数学式子表示可以表示
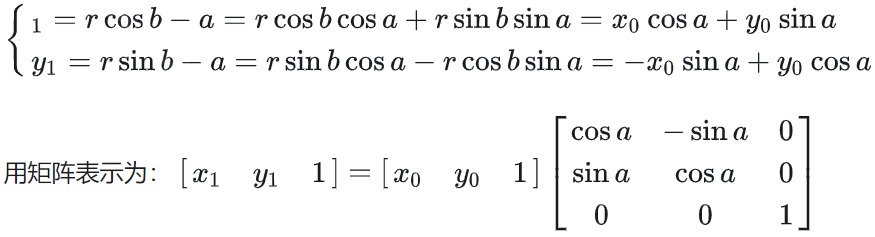
设top为旋转后最高点的纵坐标,down为旋转后最低点的纵坐标,left为旋转后最左边点的横坐标,right为旋转后最右边点的横坐标。
原图像的像素坐标要经过三次的坐标变换:
- 将坐标原点由图像的左上角变换到旋转中心
- 以旋转中心为原点,图像旋转角度a
- 旋转结束后,将坐标原点变换到旋转后图像的左上角
可以得到下面的旋转公式:(x’,y’)旋转后的坐标,(x,y)原坐标,(x0,y0)旋转中心,a旋转的角度(顺时针)
代码:
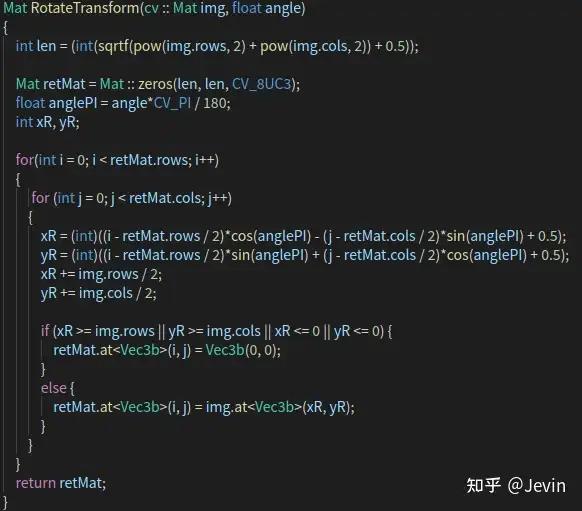
结果:
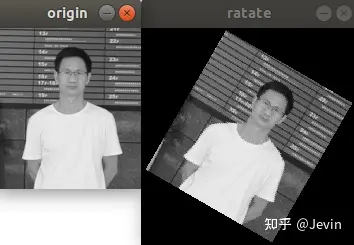
(3)仿射变换
在opencv中提供了对应的仿射变换的API接口函数warpAffine
进行仿射变换时,首先要得到仿射变换矩阵,为了实现这个功能,常常使用getRotationMatrix2D()函数用来计算二维旋转矩阵,这个变换会将旋转中心映射到它自身
Mat getRotationMatrix2D( Point2f center, double angle, double scale );
这个函数中有三个参数,第一个参数是Point2f类型的center,也就是原图像的旋转中心;第二个参数是double 类型的angle,也就是我们说的旋转角度,值得一提的是,当angle的值为正时,表示的是逆时针旋转,当angle的值为负时,表示的是顺时针旋转。第三个参数scale表示的是缩放系数
具体矩阵计算为:
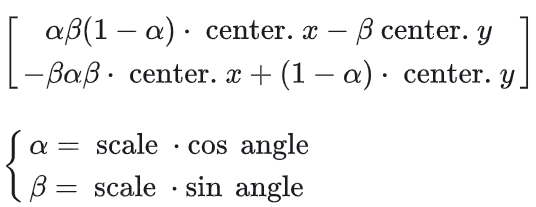
得到仿射变换矩阵后,即可调用仿射函数:
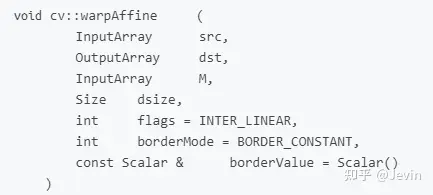
参数解释
. src: 输入图像
. dst: 输出图像,尺寸由dsize指定,图像类型与原图像一致
. M: 2X3的变换矩阵
. dsize: 指定图像输出尺寸
. flags: 插值算法标识符
代码:
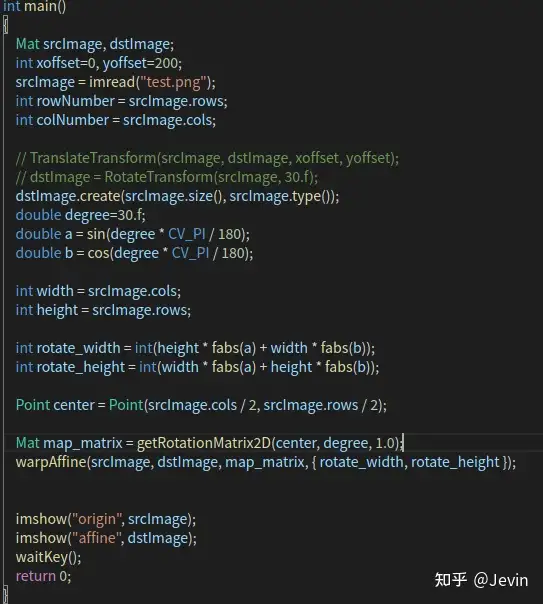
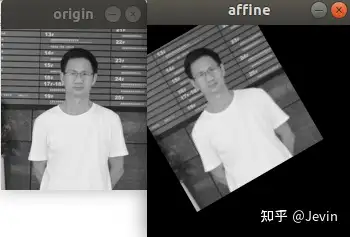
结果:
三、单应性变换
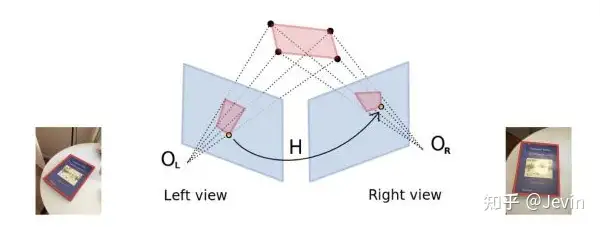
“用无镜头畸变的相机从不同位置拍摄同一平面物体的图像之间存在单应性,可以用投影变换(单应性变换)表示”
1、概念
单应(Homography)是射影几何中的概念,又称为射影变换。它把一个射影平面上的点(三维齐次矢量)映射到另一个射影平面上,并且把直线映射为直线,具有保线性质。总的来说,单应是关于三维齐次矢量的一种线性变换,可以用一个3×3的非奇异矩阵H表示,简单来说单应性变换是一个平面到另一个平面的变换关系
2、单应矩阵
用数学表达为:
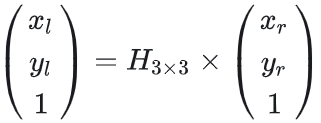
单应矩阵 3×3 的求解过程为:
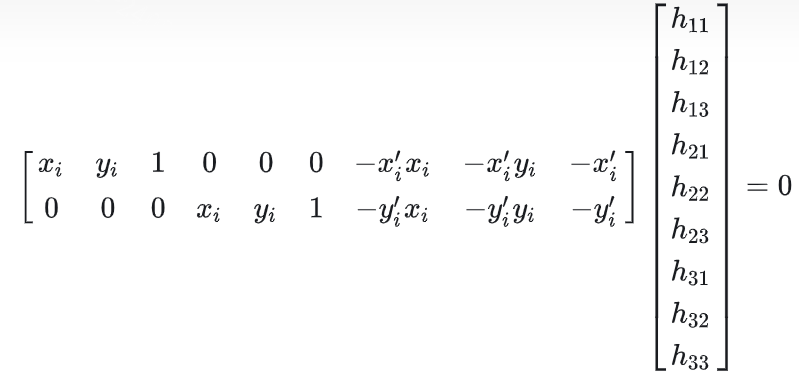
单应矩阵具有8个自由度,求解时一般添加约束 ℎ33=1 ,所以还有 ℎ11∼ℎ32 共8个未知数。由于一组匹配点 对应2组方程,那么只需要 4 组不共线的匹配点即可求解H的唯一解。
3、实验
代码:
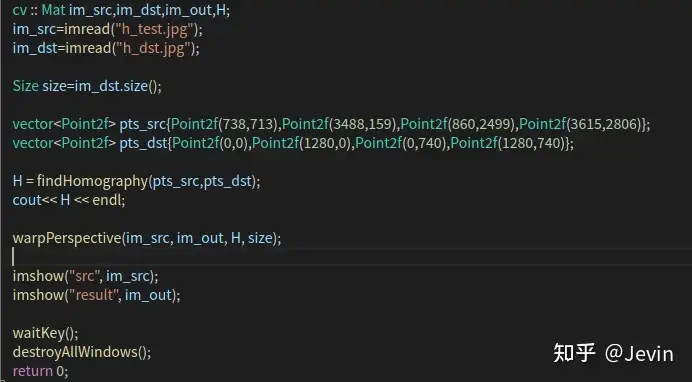
结果:

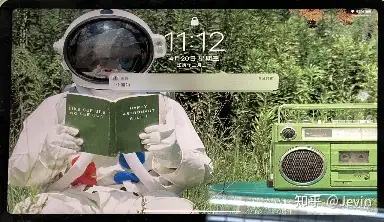
四、仿射变换与单应性变换
二者的应用场景相同,都是针对二维图片的变换。仿射变换affine是透视变换的子集,透视变换是通过homography单应矩阵实现的

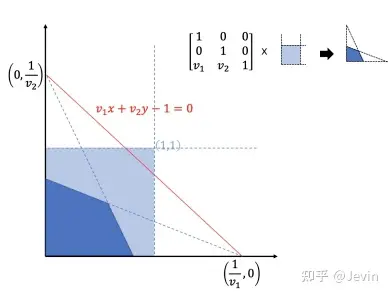
S为缩放因子
从数学的角度,homography即H阵,是一个秩为3的可逆矩阵:

由于第三行没有未知数,仿射矩阵最常用的是两行三列的形式。计算H阵需要4对不共线点,计算仿射阵只需要3对不共线的点。
affine一般比homography更稳定一些,所以可以先计算affine,然后再用affine作为homography的初始值,进行非线性优化。


