新手讲算法 归并排序 之 逆序对

1. 归并排序

  

 

 

 要点：

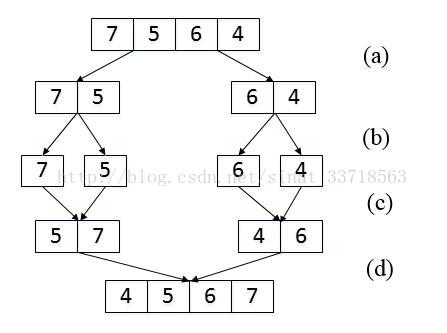
归并排序是建立在归并操作的一种有效的算法，该算法是采用 分治法 的典型应用。

 基本思想：

（1）分解：将序列每次折半划分成两个数组，直到划分成每个元素一个数组

（2）合并：将划分后的序列段两两合并后排序。

 

2.逆数对问题

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P%1000000007
输入描述:
题目保证输入的数组中没有的相同的数字

数据范围：

    对于%50的数据,size<=10^4

    对于%75的数据,size<=10^5

    对于%100的数据,size<=2*10^5
例如：
输入：1,2,3,4,5,6,7,0
输出：7

  我们可以发现，其实就是要找 每个数的左边的比他大的数一共有多少个？

（1）第一想法：两个for循环可以解决问题，时间复杂度 O(N^2),空间复杂度 O(1)。那么能做到时间更短吗？

（2）第二种做法：既然要找左边的比当前数大的一共有多少个，那么归并排序过程中正好是比较左右两边的大小，那我们在这个过程中顺便统计下左边比右边大的数量。

 

正如上图所示：

（1）a,b两步是对数组进行分解

（2）c,d两步将数组进行合并，我们可以再这个过程中统计 左边比右边数大的个数。

   我们在统计过程中，将已经合并的按照从小到大的过程进行排序，在合并的过程中，我们只用统计左边一段，对于右边一段中每个数产生的逆序对即可，因为不论左边这段，还是右边这段，在生成的过程中都是 由 更小的两个小段 合并而成的，在这个过程中已经统计过了产生的逆序数。

 

我们图解一次，统计逆序数量的合并过程。

 

 

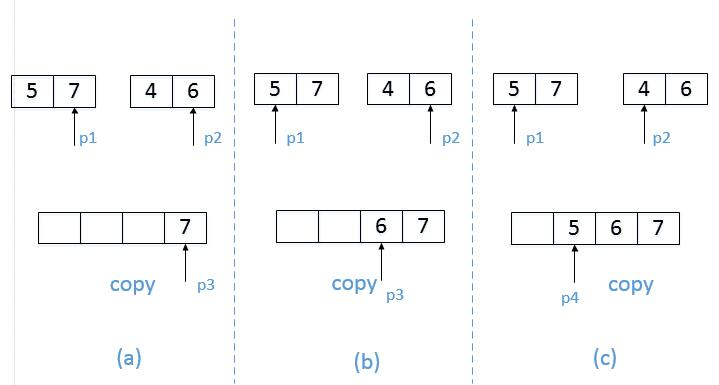
（1）左右两个子数组的最后边出发，取出 7， 6，发现7>6说明，7可以对 4，6产生逆数对，即：左边这个数 可以对 右边 没有遍历到的其他数均会产生 逆数对，因为 他比这些数都要大，统计 逆数对数量，7放入copy

（2）然后左边指针 往前走一步，取出:5，6，对于6来说没有产生逆数对且不能确定6前面的数是否会产生的逆数对，所以将6复制到copy中，

（3）右边指针往前走一步，取出：5，4，则5对于 右边没有遍历过的数（也就是4和4前面的数）都会产生逆数对，进行统计，然后，将5放入copy

（4）此时 左边数组元素全部遍历完成，右边的剩余元素 全部放入到copy中，此时copy按从小到大排序完成，逆数对统计完成。

class Solution {
public:
    int InversePairs(vector<int> data) {
        //0个或者1个
        if(data.size() == 0 || data.size() == 1) {
            return 0;
        }
        vector<int> copy = data;
        return sortMergeGetValue(data, copy, 0, data.size() - 1) % 1000000007;
    }
    
    long sortMergeGetValue(vector<int>& data, vector<int>& copy, long l, long r) {
        if(l >= r) {
            return 0;
        }
        //递归调用 归并排序
        long mid = (l + r) /2;
        long leftCounts = sortMergeGetValue(copy, data, l, mid);
        long rightCounts = sortMergeGetValue(copy, data, mid + 1, r);
        
        long count = 0;
        long i = mid;  //左半端最后面
        long j = r;  //右半段最后面
        long index = r; //copy数组最右边
        
        //当左右半段还没有合并完成时，使用while循环
        while(i >= l && j > mid) {
            //判断左半段 节点是不是 大于 右半段节点,说明左半段这个节点对于 右半段 对应节点 的前面所有节点 都会产生逆数对
            if(data[i] > data[j]) {
                count += (j - mid);
                copy[index--] = data[i--];
            } else {
                copy[index--] = data[j--];
            }
        }
        
        //如果左半段没有合并完
        for(; i>= l; i--) {
            copy[index--] = data[i];
        }
        
        //右半段没有合并完
        for(; j > mid; j--) {
            copy[index--] = data[j];
        }
        
        return count+ leftCounts + rightCounts;
    }
};

 

算法复杂度：

时间复杂度：O(N*Log(N))

空间复杂度：O(N)