如何找出数组中元素之和为特定数的最优组合

一 问题描述

给定一个含有n个元素的整形数组a，再给定一个和sum，求出数组中满足给定和的所有元素组合，

举个例子，设有数组a[5] = {1,2,3,4,5}，sum = 7，则满足和为7的所有组合是

{5,2}

{4,3}

{4,2,1}

二 解法

把sum看成一个包裹的容量，数组的元素看成石头的重量，题目可以转化为求石头的组合，使

组合内的石头刚好放进包裹。

递归解法：包裹容量为sum，先把一块重量为 m 的石头放进去，剩下包裹容量为 (sum - m)，

接下来递归地求在包裹容量为(sum - m)的前提下，有多少种石头的组合。

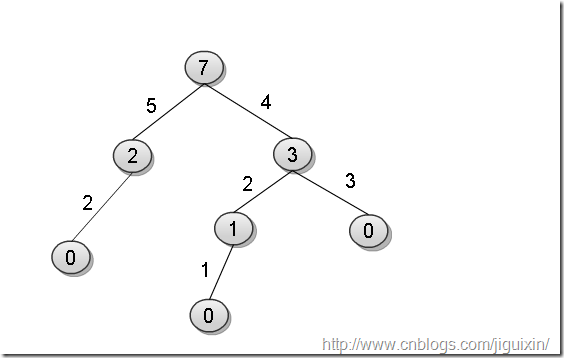
如下图所示，包容量为7，先把4放进去，剩余容量为3，容量为3的包裹，石头的组合有两种：

{2, 1}和{3}

 

算法：

1 先把石头的重量按照从小到大排序

2 用一个flag数组标记当前放入包裹的石头

3 优先选择重量大的石头放入包裹，可以减少递归的次数

三 代码实现

C++ 实现：

#include <stdio.h>  
  
#define N 5  
  
int flag[N];  
  
/* 从数组a[0]...a[t]找出和等于sum的组合 */
void how_many_sum(int *a, int sum, int t)  
{  
    int i, success;  
  
    if (sum == 0) {  
        printf("找到一个组合\n");  
        for (i = 0; i < N; i++) {  
            if (flag[i]) {  
                printf("%d,", a[i]);  
            }  
        }  
        printf("\n");  
        return;  
    }  
  
    success = 0;  
    for (i = t; i >= 0; i--) {  
        if (flag[i] == 0 && (sum - a[i]) >= 0) {  
            flag[i] = 1;  
            printf("把%d放入包裹，剩下容量为%d\n", a[i], sum-a[i]);  
            how_many_sum(a, sum - a[i], i-1);  
            printf("丢弃%d\n", a[i]);  
            flag[i] = 0;  
            success = 1;  
        }  
    }  
    if (success == 0) {  
        printf("无解\n");  
    }  
}  
  
int main()   
{  
    int a[N] = {1,2,3,4,5};  
    int sum = 7;  
    how_many_sum(a,sum,N-1);  
    getchar();  
    return 0;  
}

 

以上转自：http://blog.csdn.net/kenby/article/details/6808663 下面是我自己用C#实现的代码

C#实现：

 

private static int N = 5;
        private int[] flag = new int[N];

        [Test]
        public void CommonTest_01()
        {
             int[] a = {1,2,3,4,5};  
            int sum = 7;  
            how_many_sum(a,sum,N-1);  
        }
  
        void how_many_sum(int [] a,int sum,int t)
        {
            int i, success;
            if (sum == 0)
            {
                Debug.WriteLine("找到一个组合");
                for (i = 0; i < N;i++)
                {
                    if (flag[i] > 0)
                    {
                        Debug.Write(string.Format("{0},", a[i]));
                    } 
                }
                Debug.Write("=" + 7);
                Debug.WriteLine("");

                
                return;
            }

            success = 0;

            for (i = t;i >=0;i--)
            {
                if (flag[i] == 0 && (sum - a[i]) >= 0)
                {
                    flag[i] = 1;
                    Debug.WriteLine(string.Format("把{0}放入包裹，剩下容量为{1}", a[i], sum - a[i]));
                    how_many_sum(a, sum - a[i], i - 1);
                    Debug.WriteLine(string.Format("丢弃{0}",a[i]));
                    flag[i] = 0;
                    success = 1;  
                }
            }

            if (success == 0)
            { 
                Debug.WriteLine("无解");
            }
        }