剑指offer T4 重建二叉树

 

 二叉树的三种遍历：

前序：根节点 --> 左子树 --> 右子树

中序：左子树 --> 根节点 --> 右子树

后序：左子树 --> 右子树 --> 根节点

在前序遍历序列中，从左到右依次取一个数，并找到其在中序遍历中的位置，左边为左子树，右边则是右子树

 

 按照这种思路，编写代码如下：

 1 TreeNode* helper(vector<int> pre, vector<int> vin, int& k, int l, int r)　　
//k表示当前是前序序列中的元素的下标，l，r表示当前中序序列中的左子树或者右子树的边界
 2     {
 3         if (k == pre.size())
 4             return nullptr;
 5         if (l == r)
 6             return new TreeNode(vin[l]);
 7         int i = l;
 8         for (; i <= r; i++)　　//找到根节点的位置
 9         {
10             if (vin[i] == pre[k]) 
11                 break;
12         }
13         TreeNode* root = new TreeNode(pre[k]);
14 
15         if (i > l)
16             root->left = helper(pre, vin, ++k, l, i - 1);　　//进入左子树递归
17         if (i < r)
18             root->right = helper(pre, vin, ++k, i + 1, r);
19 
20         return root;
21 
22     }
23     
24     TreeNode* reConstructBinaryTree(vector<int> pre,vector<int> vin) {
25         if (vin.size() != pre.size() || pre.size() == 0)
26             return nullptr;
27         int k = 0;
28         TreeNode* head = helper(pre, vin, k, 0, vin.size() - 1);
29         return head;
30     }

.

 

 

 这里是分界线 　　这里是分界线 　　这里是分界线 　　这里是分界线 　　这里是分界线 　　这里是分界线 　　这里是分界线 　　这里是分界线 　　这里是分界线 　　这里是分界线 　　这里是分界线 

 

类似的一道题

 

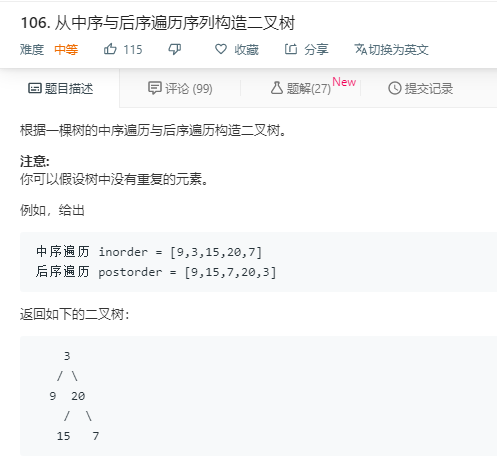
 前序遍历是从左往右依次是根节点，左子树，右子树；而后序遍历是从右往左依次是根节点，右子树，左子树。

所以上述代码只要稍作修改就行了。

 1 TreeNode* helper(vector<int>& post, vector<int>& vin, int& k, int l, int r)
 2     {
 3         if (k < 0 )
 4             return nullptr;
 5         if (l == r)
 6             return new TreeNode(vin[l]);
 7         int i = r;
 8         for (; i >= l; i--)
 9         {
10             if (vin[i] == post[k]) 
11                 break;
12         }
13         TreeNode* root = new TreeNode(post[k]);
14 
15         if (i < r)
16             root->right = helper(post, vin, --k, i + 1, r);
17         if (i > l)
18             root->left = helper(post, vin, --k, l, i - 1);
19 
20         return root;
21 
22     }
23     
24     TreeNode* reConstructBinaryTree(vector<int>& in, vector<int>& post)
25     {
26         if (in.size() != post.size() || post.size() == 0)
27             return nullptr;
28         int k = post.size()-1;
29         TreeNode* head = helper(post, in, k, 0, in.size() - 1);
30         return head;
31     }

 

 

posted @ 2019-09-24 14:34  寅鸷  阅读(160)  评论(0)  编辑  收藏  举报