排序

 

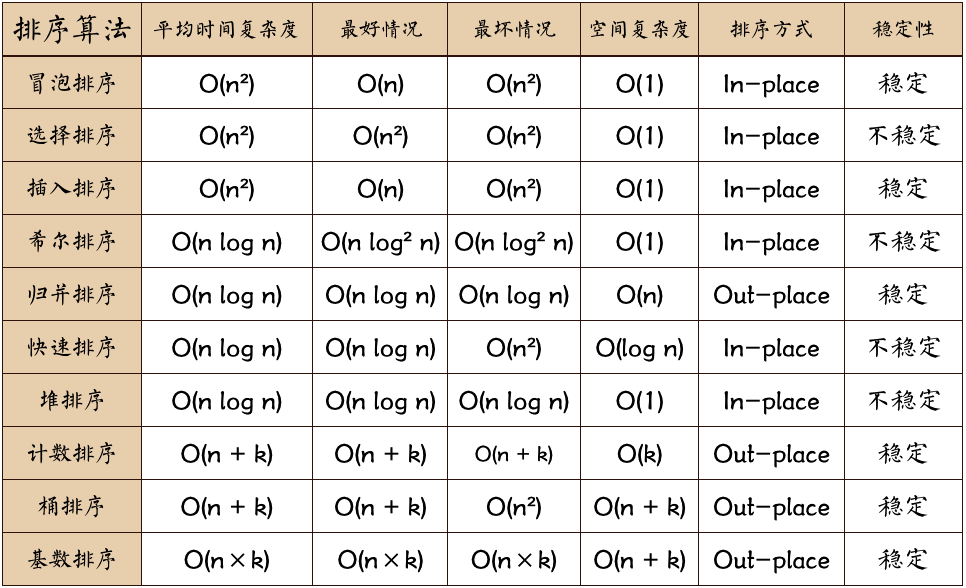
 强烈推荐一篇非常好的文章：http://www.runoob.com/w3cnote/bubble-sort.html

 

快排

快速排序算法是二分法的一种典型的应用，其平均时间复杂度为O(nlogn)

快排有两种操作方式，第一种为交换法，第二种为赋值法，我个人觉得赋值法比较容易理解所以这里就仅讲解赋值法。

由于个人水平有限，可以参考我老师的博客https://blog.csdn.net/qq_30277239/article/details/98038698

 

 

先看代码：

void quickSort(vector<int>& arr, int l, int r)
{
    if (l >= r) return;
    int head = l, tail = r;
    int pivot = arr[l];
    while (l < r)
    {
        while (l<r && arr[r]>pivot) r--;
        arr[l] = arr[r];
        while (l < r && arr[l] < pivot) l++;
        arr[r] = arr[l];
    }
    arr[r] = pivot;
    quickSort(arr, head, r - 1);
    quickSort(arr, r + 1, tail);
}

int main()
{
    vector<int> vec = { 5,9,1,3,6,10,4,2 };
    quickSort(vec, 0, vec.size()-1);
    return 0;
}

 

算法思想：选定锚点 ----> 将大于锚点的放在右边，小于锚点的放在左边  ---->  递归

每次调用quicksort函数时都对数组进行排序，返回锚点的位置。

 

如图，首先以左边第一个数作为锚点，选定锚点之后将锚点保存下来，因为之后会被覆盖掉。

注意当我们以左边第一个数作为锚点时我们就要先从右边开始查找第一个小于锚点的数

找到第一个小于锚点的数就立刻进行赋值，然后再从左边开始找大于锚点的数，

 

 

 如图先找到2，将2赋值给arr[left]，然后从左边开始找到9赋值给arr[right]。

重复上述步骤：

第一步的最终结果

 

 令arr[r] = pivot

 

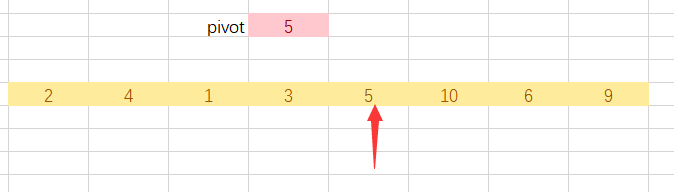
 最后返回pivot锚点所在位置的index，然后以这个index为标志位，进行左右递归就行了。

 

优化方法：

 

按照如上方法，每次都是以最左边的或者最右边的数为锚点的，这样做存在一个不稳定的因素，那就是如果每次选取的锚点可能是最大或者最小值。

这样算法的时间复杂度就退化到了O(n2)了，我们可以使用去中间值方法，再right，mid， left三个数中去中间值，然后把中间值换到left的位置，运用上述相同的代码便可提高算法的稳定性。

 

 

 

堆排序

堆排序两步走：1.构建堆  2. 调整堆

首先堆是一个完全二叉树

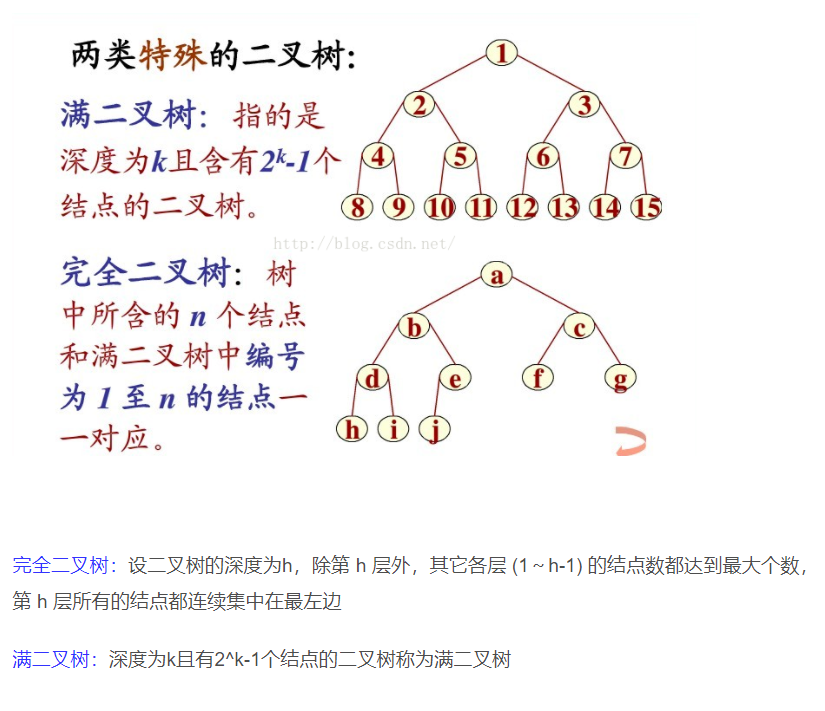
堆排序二叉树节点按照层次遍历的顺序（从上至下，从左至右），依次按照数组的下标进行编号并放入数组的值

完全二叉树的最后一个根节点为  root =（ size / 2 - 1 ），

假设当前节点编号为 idx

左右叶子节点数组下标分别为    left = （ 2 * idx + 1 ）      right = （ left + 1 ）

 

 1 vector<int> HeapSort(vector<int>& vec)
{
    //构建大根堆
    for (int i = vec.size() / 2 - 1; i >= 0; i--)
    {
        adjustHeap(vec, i, vec.size());
    }

    //调整大根堆，将堆顶元素和最后一个数交换
    for (size_t i = vec.size(); i > 0; i--)
    {
        swap(vec[0], vec[i-1]);
        adjustHeap(vec, 0, i-1);
    }
    return vec;
}

void adjustHeap(vector<int>& vec, int i, int size)
{
    int temp = vec[i];
    for (int k = 2 * i + 1; k < size; k = 2 * k + 1)
    {
        if (k + 1 < size && vec[k] < vec[k + 1])
        {
            k++;    //找到左右子节点中的最大值
        }

        if (vec[k] > temp)
        {
            vec[i] = vec[k];
            i = k;
        }
        else
        {
            break;
        }
    }
    vec[i] = temp;
}