树、二叉树、查找算法总结

树、二叉树、查找算法总结。

一、思维导图

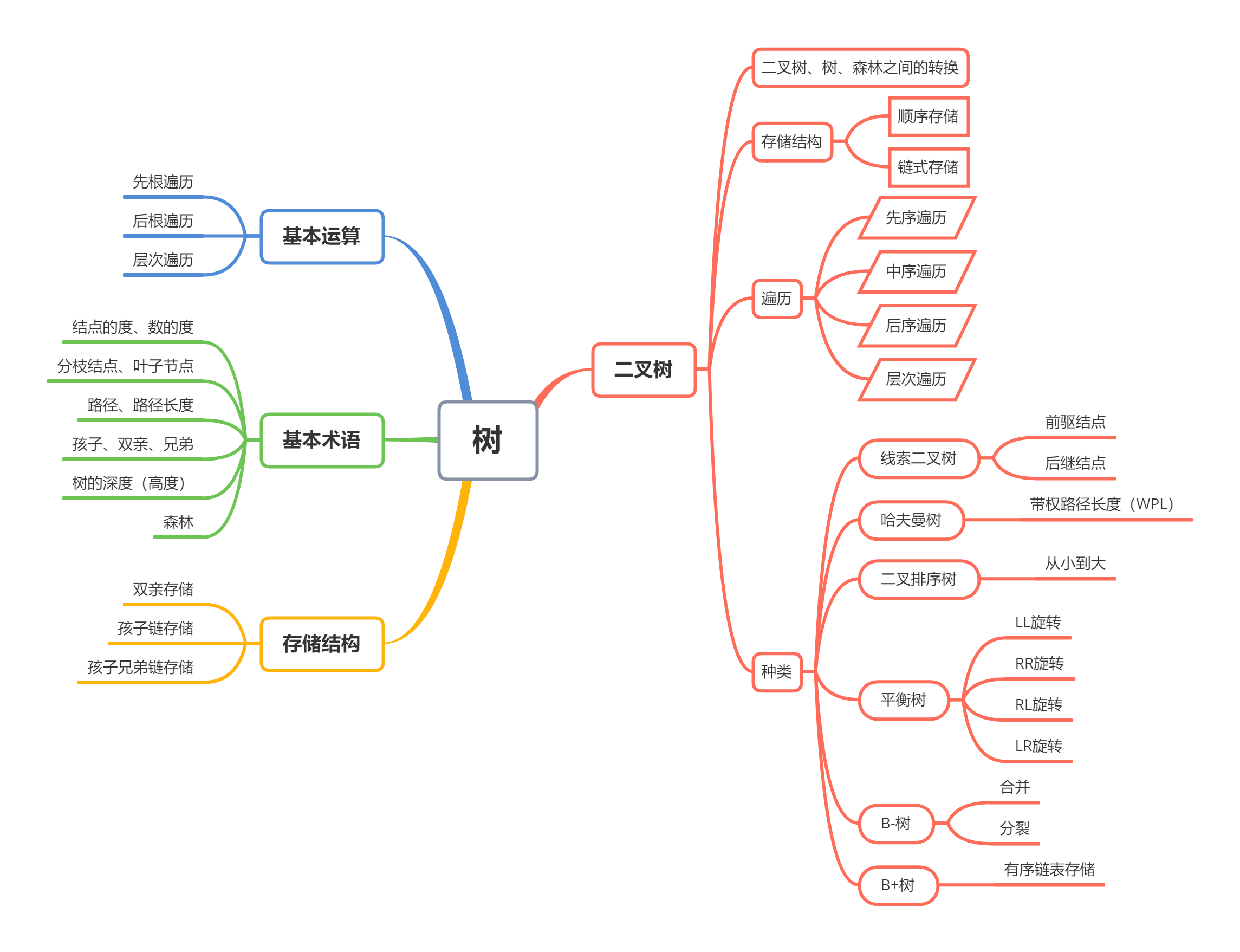
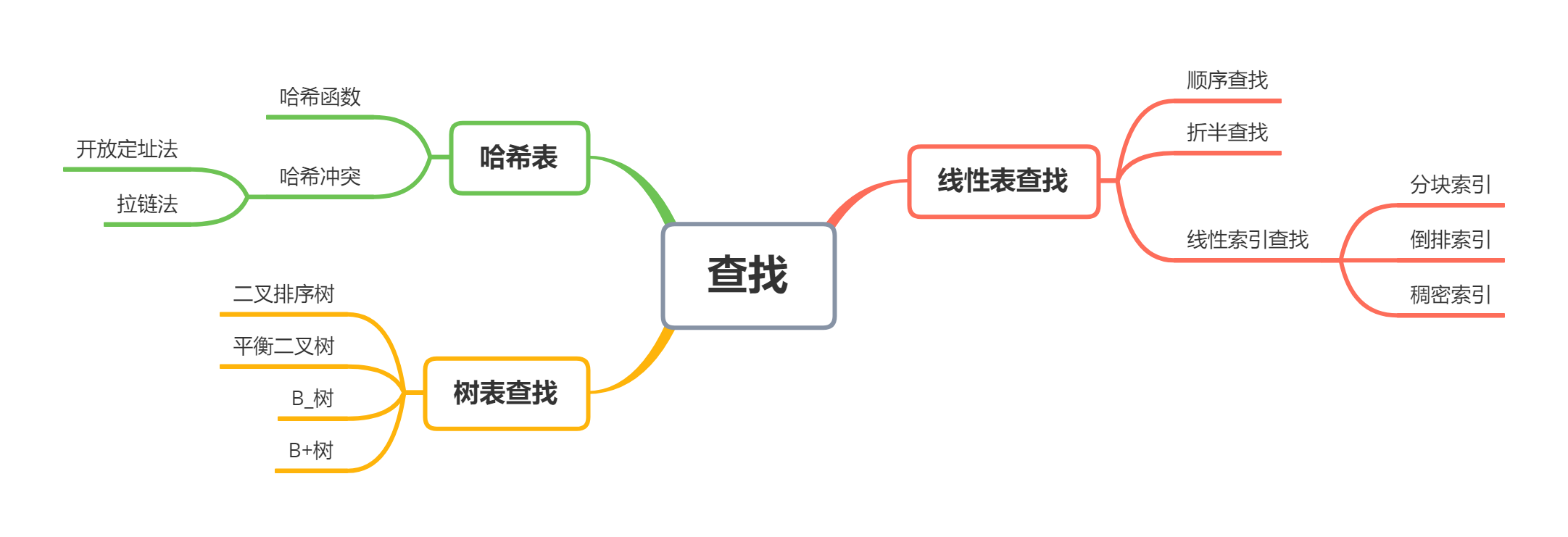
二、概念笔记

1.结点的度与树的度：

树中某个结点的子树的个数称为该结点的度。一个树中所有结点的度中的最大值称为树的度，度为m的树称为m次树。

2.分枝结点、子叶结点：

度不为零的结点叫分枝结点，度为零的结点叫子叶结点。

3.路径、路径长度：

从一个结点到另一个结点的轨迹叫做路径，轨迹包含的结点数减1就是路径长度。

4.孩子结点、双亲结点、兄弟结点：

一个结点的后继结点叫做孩子结点，相应的，这个结点就是后继结点的双亲结点，双亲结点相同的结点互为彼此的兄弟结点。

5.树的遍历：

​ 1）先根遍历：先访问根结点，再从左往右遍历根结点的子树。

​ 2）后根遍历：先从左往右遍历根结点的子树，再访问根结点。

​ 3）层次遍历：从根结点开始，从上到下，从左到右，一层一层地访问每个结点。

6.树的存储结构：

​ 1）双亲存储结构：

typedef struct
{  Elemtype data;	//结点的值
   int parent;		//双亲的位置
} PTree[maxsize];

​ 2）孩子链存储结构：

typedef struct node
{  Elemtype data;		//结点的值
   struct node * sons[maxsize];		//孩子的位置
} TSonNode;

​ 3）孩子兄弟链存储结构：

typedef struct node
{  Elemtype data;		//结点的值
   struct node * hp;		//兄弟的位置
   struct node * vp;		//孩子的位置
} TSonNode;

7.森林、树转换为二叉树：

树中所有的兄弟之间加一条线，再删除他们与原来双亲之间的连线，就可以将树转化为二叉树。

8.二叉树转换为森林、树：

将根结点与其右孩子之间的连线切断，重复这个操作，形成森林，直到所有的二叉树的根结点都没有右孩子。将一个结点的左孩子的所有右孩子都连接到这个结点上，再删除他们之间原有的结点，就可以将二叉树转化为树，这些树结合在一起就是二叉树转换为森林的操作。

9.二叉树的遍历：

​ 1）先序遍历：先访问根结点，再访问左孩子，再访问右孩子。

​ 2）中序遍历：先访问右孩子，再访问根结点，再访问左孩子。

​ 3）后序遍历：先访问左孩子，再访问右孩子，再访问根结点。

​ 4）层次遍历：从根结点开始，从上到下，从左到右，一层一层地访问每个结点。

10.线索二叉树：

当某个结点的左指针或右指针为空时，将指针指向线性序列中的前驱结点或后继结点，这样的指针称为线索，创建线索的过程称为线索化，线索化的二叉树被称为线索二叉树。

11.哈夫曼树：

带权路径长度WPL最小的二叉树称为哈夫曼树WPL=所有（叶子结点的权值*路径长度）之和。

12.二叉排序树：

将新进入树的结点从根结点开始进行比较，小于结点值的话就与当前结点的左孩子比较，大于结点值的话就与当前结点的右孩子比较，最后得到一个中序排列为从小到大的排序。

13.平衡树：

每个结点的左、右子树的高度最多相差1的二叉树叫做平衡树。

14.折半查找：

效率很高的查找方法，但是要求线性表是有序表。

15.索引存储结构：

在存储数据的同时，还建立附加的索引表，每一项称为索引项，形式一般为关键字、地址。

三、疑难问题

1）层次遍历代码：

在层次遍历代码时，我不知道要怎样才能达到一层层的输出一个二叉树，因为还在想着之前学到的递归，所以一点头绪都没有。

解决：利用队列的属性来帮助我们达到层次遍历，当队不为空时，就将队头的结点出队，进行判断，有左孩子的话左孩子进队，有右孩子的话右孩子进队，这样就可以达到一层一层的输出二叉树了。

2）倒排索引：

在讲倒排索引的时候，没有明白倒排索引的机制是什么。

解决：在老师有讲了一遍，自己又去网上查找了一些讲解，通过输入到搜索引擎中的关键字的组合来寻找内容与多个关键字相同的文档，是在搜索引擎中运用比较广泛的一种索引方式。