java 堆排，优先级队列，归并排序

堆排

堆排是基于二叉树而得来的

例如：对一个数组

                          可以转为二叉树：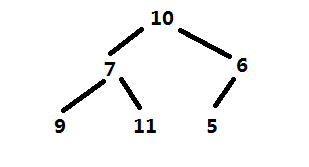      

                         二叉树特性父节点为 i ，  左叶子节点为2i+1；右叶子节点为2i+2;

步骤分解：

1. 先从第一个非叶子节点（即下标为(length-1-1）/2 即6）开始，把大的值往父节点调整

    经过一轮调整之后 最大的值此时在根节点处（即arr[0]）：

                                                                                   

2.根节点数和数组最后一个元素进行交换，此时数组中最大的值在最后一位，一个有序元素产生，

3.反复进行此过程，再次交换时和未被排序的最后一个元素交换，直至数组有序。

堆排的时间复杂度：无论哪种情况 都是 nO（log2n）

          空间复杂度：O（1）

　　　稳定性：不稳定。

 

源码

private static void heapSort(int[] arr) {
        int n = arr.length - 1;

        // 从第一个非叶子节点开始，把大值往父节点调整
        for (int i = (n - 1) / 2; i >= 0; --i) {
            adjust(arr, i, arr.length);
        }
        for (int i = n; i >= 0; --i) {
            //0 <=> i 它们的值进行交换
            int tmp = arr[0];
            arr[0] = arr[i];
            arr[i] = tmp;
            //再继续进行堆的调整 adjust
            adjust(arr,0,i);
        }
    }

    /**
     * 堆的调整函数，把每一个节点，和其左右孩子节点的最大值放到当前节点处
     *
     * @param arr
     * @param i
     * @param length
     */
    private static void adjust(int[] arr, int i, int length) {
        int temp = arr[i];
        for (int j = 2 * i + 1; j < length; j = 2 * j + 1) {
            if (j+1<length&&arr[j + 1] > arr[j]) {
                    j++;
            }
            if (arr[j] > temp) {
                arr[i] = arr[j];
                i=j;
            }else break;
        }
        arr[i]=temp;
    }

优先级队列

优先级队列=>基于大根堆实现

 

public class PriorityQueue<T extends Comparable<T>> {
    private T[] queue;
    private int index; // 记录有效元素的个数

    public PriorityQueue(){
        this.queue = (T[])new Comparable[10];
    }

    // 入优先级队列
    public void push(T val){
        if(full()){
            this.queue = Arrays.copyOf(queue, queue.length*2);
        }

        if(index == 0){
            queue[index] = val;
        } else {
            siftUp(index, val); // 新插入的元素，要进行堆的上浮操作
        }
        index++;
    }

    /**
     * 堆的上浮函数
     * @param i
     * @param val
     */
    private void siftUp(int i, T val) {
        while(i > 0){
            int j = (i-1)/2;
            if(queue[j].compareTo(val) < 0){
                queue[i] = queue[j];
                i = j;
            } else {
                break;
            }
        }
        queue[i] = val;
    }

    // 出优先级队列
    public T pop(){
        if(empty())
            return null;

        T oldval = queue[0];
        --index;
        if(index > 0){
            siftDown(0, queue[index]); // 删除元素，进行堆的下沉操作
        }
        return oldval;
    }

    /**
     * 堆的下沉函数
     * @param i
     * @param val
     */
    private void siftDown(int i, T val) {
        for(int j=2*i+1; j<index; j=j*2+1){
            if(j+1 < index && queue[j+1].compareTo(queue[j]) > 0){
                j++;
            }

            if(queue[j].compareTo(val) > 0){
                queue[i] = queue[j];
                i = j;
            } else {
                break;
            }
        }
        queue[i] = val;
    }
    boolean full(){
        return index == queue.length;
    }

    boolean empty(){
        return index == 0;
    }

 

 

 

归并排序

    归并排序为外部排序，适用于内存有限制，数据无法一次性放入内存的情况

       基本思路：采用分治法，将数组分为A B两部分，可以将A，B组各自再分成二组。依次递归，当分出来的小组只有一个数据时，可以认为这个小组组内已经达到了有序，然后再递归合并相邻的二个小组就可以了。

        时间复杂度：O（nlog2n）

         空间复杂度：O（n）

         稳定性：稳定

 

源码

 

   //i=0；j=arr.length-1.
 private static void mergeSort(int[] arr, int i, int j) {
        if(i < j)
        {
            int mid = (i+j)/2;
            /**
             * 以下的操作，先进行数组划分，直到划分为单个元素以后，逐级向上回溯
             * 的时候，进行合并操作
             */
            mergeSort(arr, i, mid);
            mergeSort(arr, mid+1, j);
            merge(arr, i, j); // 合并两个有序的序列
        }
    }

    /**
     * 合并两个有序的序列
     * @param arr
     * @param low
     * @param high
     */
    private static void merge(int[] arr, int low, int high) {
        int[] tmp = new int[high-low+1];
        int mid = (low+high)/2;  // i-mid mid+1-j
        int i=low; // [i, mid]区间
        int j=mid+1; // [mid+1, high]区间
        int idx=0;

        // 3 12        5 8
        while(i <= mid && j <= high){
            if(arr[i] > arr[j]){
                tmp[idx++] = arr[j++];
            } else {
                tmp[idx++] = arr[i++];
            }
        }

        while(i <= mid){  //
            tmp[idx++] = arr[i++];
        }

        while(j <= high){
            tmp[idx++] = arr[j++];
        }

        // 把tmp里面合并的有序段再写回arr的[low,high]
        for(int k=low; k<=high; ++k){
            arr[k] = tmp[k-low];
        }
    }