四元数小总结
四元数记法：
一个四元数包含一个标量分量和一个3D向量分量。记标量为w，记向量为v或分开的x,y,z。如下：
[w,v]
[w,(x,y,z)]
四元数与复数：
四元数扩展了复数系统 ，它使用三个虚部i,j,k。它们的关系如下：
i2=j2=k2=-1
ij=k,ji=-k
jk=i,kj=-i
ki=j,ik=-j
一个四元数[w,(x,y,z)]定义了复数 w+xi+yj+zk。
四元数和轴-角对：
四元数能被解释为角位移的轴-角对方式。其公式为下：
设向量n为旋转轴，θ为绕轴旋转的量。
q=[cos(θ/2) sin(θ/2)n]
=[cos(θ/2) (sin(θ/2)nx sin(θ/2)ny sin(θ/2)nz)]
负四元数：
-q=[-w (-x -y -z)]=[-w -v]
q和-q代表的实际角位移是相同的，很奇怪吧！如果我们将θ加上360度的倍数，不会改变q代表的角位移，但它使q的四个分量变负了。因此，3D中的任意角位移都有两种不同的四元数表示方式，它们互相为负。
单位四元数：
几何上存在2个单位四元数：[1,0]和[-1,0]。它们的意义是：当旋转角为360度的整数倍时，方位并没有改变，并且旋转轴也是无关紧要的。
数学上只有一个单位四元数：[1,0]。任意四元数q乘以单位四元数[1,0]仍为q。
四元数的模：
公式如下：
||q||=||[w (x y z)]||=sqrt(w2+x2+y2+z2)
=||[w v]||=sqrt(w2+||v||2)
几何意义：
||q||=sqrt(cos(θ/2)2+sin(θ/2)2||n||2)
若n为单位向量，则：||q||=1
四元数共轭：
q*=[w -v]=[w (-x -y -z)]
四元数的逆：
q-1=q*/||q||
但我们只使用单位四元数，故q-1=q*
几何解释：使向量v反向，则旋转方向也反向了。因此q绕轴旋转θ角，而q*沿相反的方向旋转相同的角度。
四元数乘法（叉乘）：
[w1 v1][w2 v2]=[w1w2-v1v2 w1v2+w2v1+v2×v1]
四元数叉乘满足结合律但不满足交换律：
(ab)c=a(bc)
ab!=ba
四元数乘积的模等于模的乘积：
||q1q2||=||q1|| ||q2||
四元数乘积的逆等于各个四元数的逆以相反的顺序相乘：
(ab)-1=b-1a-1
如何用四元数将3D点绕轴旋转：
让我们“扩展”一个标准3D点(x,y,z)到四元数空间，通过定义四元数p=[0, (x,y,z)]即可。设q为我们讨论的旋转四元数形式[cos(θ/2) sin(θ/2)n]，n为旋转轴，单位向量，θ为旋转角。你会惊奇地发现，执行下面乘法可使3D点p绕n旋转：
p'=qpq-1
四元数乘法的优势在哪？对点p先执行a旋转再执行b旋转：
p'=b(apa-1)b-1=(ba)p(a-1b-1)=(ba)p(ba)-1
注意，先进行a旋转再进行b旋转等价于执行乘积ba代表的单一旋转。因此，四元数乘法可用来连接多次旋转，这和矩阵乘法效果一样。
四元数的“差”：
定义：从一个方位到另一个方位的角位移。
如给定方位a和方位b，求a到b的角位移d。用四元数表示为：ad=b => d=a-1b
四元数点乘：
q1·q2=[w1 v1]·[w2 v2]=w1w2+v1·v2
几何解释：类似于向量点乘的几何解释，两四元数点乘绝对值越大，其代表的角位移越相似。
四元数的对数：
首先，令α=θ/2，||n||=1，则q=[cosα nsinα]=[cosα xsinα ysinα zsinα]，公式如下：
log q=log[cosα nsinα]=[0 αn]
注意log q的结果，它一般不是单位四元数。
四元数的指数：
设四元数p的形式为[0, αn]，n为单位向量：
p=[0 αn]=[0 (αx αy αz)]
||n||=1
公式如下：
exp p=exp([0 αn])=[cosα nsinα]
根据定义，exp p问题返回单位四元数。
四元数指数运算为四元数对数运算的逆运算：
exp(log q)=q
四元数与标量相乘：
kq=k[w v]=[kw kv]
=k[w (x y z)]=[kw kx ky kz]
四元数求冥：
qt=exp(tlog q)
几何意义：对数运算log q提取了轴n和角度θ；接着和指数t进行标量乘时，结果是θ乘以t；最后，指数运算“撤消”了对数运算，以tθ和n重新计算w和v。
求四元数冥的代码如下：
1 /// <summary> 2 /// 四元数求冥 3 /// </summary> 4 /// <param name="e">指数</param> 5 /// <param name="w,x,y,z">四元数输入，输出</param> 6 static void Calc(float e, ref float w, ref float x, ref float y, ref float z) 7 { 8 // 检查单位四元数的情况，避免除零 9 if (Mathf.Abs(w) < 0.9999f) 10 { 11 // 提取半角(θ/2) 12 float alpha = Mathf.Acos(w); 13 // 计算新的alpha值 14 float newAlpha = alpha * e; 15 // 计算数的w值 16 w = Mathf.Cos(newAlpha); 17 float multi = Mathf.Sin(newAlpha) / Mathf.Sin(alpha); 18 // 计算新的xyz值 19 x *= multi; 20 y *= multi; 21 z *= multi; 22 } 23 }
四元数插值——"slerp"：
当今3D数学中四元数存在的理由是由于一种称作slerp的运算，即球面线性插值（Spherical Linear Interpolation）。slerp运算非常有用，因为它可以在两个四元数之间平常插值。slerp插值避免了欧拉角插值的所有问题（如万向锁）。
求法一：
设开始与结束的四元数为q0，q1，插值变量设为t，t在[0, 1]之间变化 。则slerp函数定义为: slerp(q0,q1,t)
计算此函数的思路如下：
△a=a1-a0
lerp(a0,a1,t)=a0+t△a
四元数中，
1. 计算差值：q0△q=q1 => △q=q0-1q1
2. 取插值的一部分，应用求冥的办法，即(△q)t
3. 初始值加上插值的一部分，应用四元数乘法。
综上，公式如下：
slerp(q0,q1,t)=q0(q0-1q1)t
这是理论上的公式，实践中，将使用更有效的一种办法。
求法二：
slerp的基本思想是沿着4D球面上连接两个四元数的弧插值。
可以把这种思想表现在平面上，如向量v0,v1都是单位向量，w是之间的夹角，t在[0,1]区间，求vt：
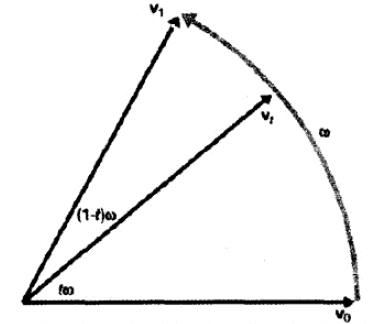
求得：vt=(sin(1-t)w/sinw)v0+(sintw/sinw)v1
将同样的思想扩展到四元数上，重写slerp可得：
slerp(q0,q1,t)=(sin(1-t)w/sinw)q0+(sintw/sinw)q1
可以用点乘来计算两个四元数间的“角度”。
这里有2点需要考虑：第一，四元数q和-q代表相同的方位，但它们作为slerp参数时可能导致不一样的结果，这是因为4D球面不是欧氏空间的直接扩展。而这种现象在2D和3D中不会发生。解决方法是选择q0和q1的符号使得点乘q0·q1的结果是非负。第二个要考虑的是如果q0和q1非常接近，sinθ会非常小，这时除法可能会出现问题。为了避免这样的问题，当sinθ非常小时使用简单的线性插值。
