插值法:
直线公式:
假设有某个二次多项式函数 ,已知它在三个点上的取值为:
,已知它在三个点上的取值为:
要求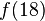 的值。
的值。
首先写出每个拉格朗日基本多项式:
然后应用拉格朗日插值法,就可以得到 的表达式(
的表达式( 为函数
为函数 的插值函数):
的插值函数):
此时代入数值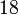 就可以求出所需之值:
就可以求出所需之值: 。
。
C算法:
引用 :实验二:Lagrange拉格朗日插值法之C语言代码 - Chen_dSir的博客 - CSDN博客 https://blog.csdn.net/Chen_dSir/article/details/70236987
ypedef struct stPoint
{
double x;
double y;
} Point
#define Dots_N 5
Point Dots[Dots_N];
/*n 为插入的点的个数,tmp为拉格朗日基函数,x为要插入的点,lagrange为插值运算后返回的值。*/
double f32Lagrange_LineSert(Point *points,u8 n,double x)
{
u8 i ,j;
double tmp,lagrange=0;//这个x是你将要计算的f(x)插值点,tmp是拉格朗日基函数,larange是根据拉格朗日函数得出f(x)的值
for(i=0;i<=n;i++)
{
for(j=0,tmp=1;j<=n;j++)
{
if(j!=i) //去掉xi与xj相等的情况,范德蒙行列式下标就是j!=k,相等分母为0就没意义了
{
tmp=tmp*(x-points[j].x)/(points[i].x-points[j].x);//这个就是套公式tmp是拉格朗日基函数
}
}
lagrange=lagrange+tmp*points[i].y; //最后计算基函数*y,全部加起来,就是该x项的拉格朗日函数了
}
return lagrange;
}



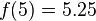
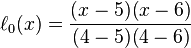
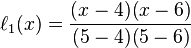

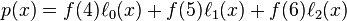
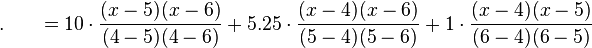
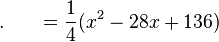


【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· Manus的开源复刻OpenManus初探
· AI 智能体引爆开源社区「GitHub 热点速览」
· 三行代码完成国际化适配,妙~啊~
· .NET Core 中如何实现缓存的预热?
2017-12-25 蜂鸣器
2017-12-25 多机通讯
2017-12-25 RS485的自动发送与布线
2017-12-25 MODBUS移植的参考文章