算法分析 - 学习笔记
这篇博文主要会讲述基础的算法分析,对于算法分析主要是针对算法运行时间进行分析。
几个需要注意的读法:Omega(Ω),Theta(Θ)和大O符号。
一、算法分析 - 最坏情况分析法
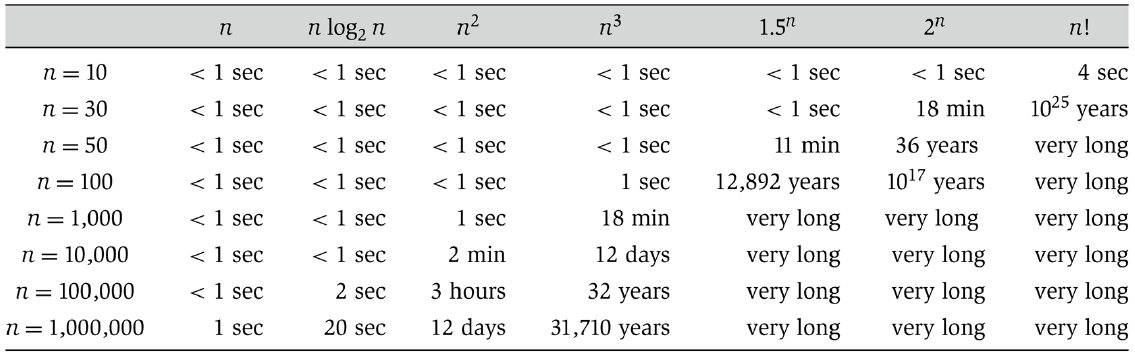
算法分析其实主要针对两方面,但是平时更多地所讲的一个算法的好坏通常是通过算法运行时间来衡量,如若一个算法运行时间短,则说明这个这个算法的针对某个问题的执行效率不错,反之则说明算法较为低效。前面所说的算法针对运行时间衡量结果大部分指的更多是是效率问题,好坏非一个绝对的标准,针对不同问题,算法执行的时间也不同,并无法绝对说这个算法好还是那个算法好,基本要从实际出发。一般而言,我们所期望的是随着输入数量(input size: N)的成倍增长,算法运行效率应当仅慢常数因子c(constant factor c)。而我们在分析算法时很多时候用的是最坏情况分析法(Worst-case Analysis),亦称最坏情况运行时间(Worst-case Running Time)。而一个算法是有效率的(efficient)如果它的运行时间是多项式时间,也就是说针对某一个问题的算法运行时间不大于问题大小的多项式倍数。下图是不同算法随着输入大小的增加所需要运行时间:
二、渐近增长阶
假设算法的最坏情况运行时间我们记作T(n),这里有另外一个函数f(n),如果存在下述的三种情况,我们则称之为上界、下界和既是上界也是下界。
渐近上界:如果存在一个常数c > 0和n0 > 0以至于所有n > n0 都有T(n) < c · f(n),我们则称之为T(n)是O(f(n)),f(n)为T(n)的上界。
举个例子:假设我们有一个算法的运行时间为T(n) = pn2 + qn + r,这里的p、q和r都是大于0的数,那么如果我想说这个函数是服从O(n2)的话,则可以写成T(n) = pn2 + qn + r ≤ pn2 + qn2 + rn2 ≤ (p + q + r) · n2 ,这个则符合上述定义。因此我们称T(n)是O(n2) 。
渐近下界:反之,对于任意大的输入,如果存在一个函数f(n)致使T(n) ≥ ε · f(n)(亦称之为Ω(f(n))),我们则称之为渐近下界。
举个例子:T(n) = pn2 + qn + r ≥ pn2 ≥ pn(p = ε),所以T(n)是Ω(n),也就是f(n) = n是T(n)的下界。
既是上界也是下界:从上面两个式子我们可以看出f(n) = n2 是T(n)的上界也是下界,我们称之为Θ(n2)。
三、例子
这里主要列举几个算法来表述不同的运行时间。
3.1 线性时间(linear time)
线性时间指的是算法的运行时间最多为一个常数因子乘于输入的大小,最常用来表示的一个算法就是查找一个数列中的最大数及合并两个已经排好序的数列,这里仅展示伪代码,因为实现都较为简单,可以尝试用自己喜欢的语言复现。
# 寻找最大数
max <- a1
for i = 2 to n:
if ai > max:
max = ai
# 合并两个排好序的数
i = 1, j = 1
final_output = []
while (both list are not empty):
if ai <= bj:
final_output.append(ai)
i += 1
else:
final_output.append(bj)
j += 1
final_output.append(remainder of the nonempty list)
3.2 对数时间(n log (n)) - 归并排序(此处是Python代码实现)
def MergeSort(lst): if len(lst) == 1: return lst half_length = len(lst) // 2 left_lst = MergeSort(lst[:half_length]) right_lst = MergeSort(lst[half_length:]) return Merge(left_lst, right_lst) def Merge(left_lst, right_lst): """Merge Function for Merge Sort""" l_index, r_index = 0, 0 lst = [] while l_index < len(left_lst) and r_index < len(right_lst): if left_lst[l_index] < right_lst[r_index]: lst.append(left_lst[l_index]) l_index = l_index + 1 else: lst.append(right_lst[r_index]) r_index = r_index + 1 lst = lst + left_lst[l_index:] lst = lst + right_lst[r_index:] return lst
还有关于O(n2)、O(n3)等其他的运行时间的例子,此处就不一一举例,有兴趣的朋友可以参考下面的列出的书籍并按照自己喜欢的编程语言实现一遍。
如若有哪里讲的不对或者读者有更好的建议,欢迎指出,非常感谢!
参考:
《算法设计》,Jon Kleinberg / Éva Tardos,清华大学出版社,2007。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号