决策树

　　一、决策树

1、基本流程

 有三种情况会让递归停止：1、当前节点包含的样本属于同一类别，无需划分。2、属性集为空，所有样本在所有属性上取值都一致，返回的是这个节点样本最多的类别。3、当前节点样本为空，这时候返回父节点的样本最多的类别

 

2、划分选择

1）熵：

 

2）信息增益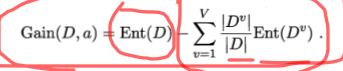：，信息增益最大的就是最优的选择，这就是ID3算法

3）信息增益率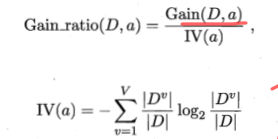：，在信息增益基础上，消除由于特征取值过多，导致信息增益变大的影响。同时由于信息增益率会偏向于取值较少的特征，因此这里并不是直接使用信息增益率，而是在候选划分属性中找到信息增益高于平均水平的属性，再从中选择信息增益率最高的。这个就是从ID3算法发展上来的C4.5算法

4）基尼系数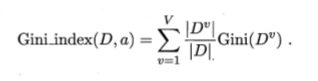：基尼系数表示随机取两个样本，其类别不一致的概率，基尼系数越小代表概率越小，纯度越高。这个就是CART算法

5）上面讲的都是分类树的划分标准，还有回归树的划分标准如下：使用的是最小误差平方和

 

 

 3、评价函数（也就是损失函数）

由于决策树最终分类只是又叶子节点的类别来决定的，所以直接计算叶子节点的熵加权累加，就可以当做损失函数，熵越小，累加越小，代表损失函数越小

这里需要了解，真正对分类起作用的是叶子结点的情况，因此对于叶子节点中，可以计算每个叶子节点的熵，再将这棵树所有的叶子节点的熵进行加权求和（这是因为每个叶子的样本数不一样），这样就得到这棵树的评价函数

（其实这里的评价函数有一点损失函数的感觉，随着树越来越生长，损失值应该越来越小）

 三种算法的比较

 

4、防止过拟合 

防止过拟合的方法：1、设置树的深度，比如最多5层；2、设置叶子结点的最少样本数；3、预剪枝、后剪枝

预剪枝：在生成过程中剪枝：比如叶子节点最少样本多少就停止，熵小于多少就停止

后剪枝：依次从T0剪枝到T1剪枝到T2剪枝到T3最后到Tk，一共得到K颗树，用验证集对这K棵树进行评价，选择损失函数最小的就可以，所以问题现在就在，如何选择节点来做剪枝，也就是每次应该先选择哪一个节点呢。这就需要前面的评价函数来确定剪枝系数，就是下面的

1、树越生长，损失值越小，所以c（T）<c(t) 没生长的树，但是如果树一直长，就会导致决策树越复杂，我们为了防止过复杂，并不能直接使用损失函数C（t）的值来做对比，因为如果只用这个值对比，肯定最大的树损失最小也就最好，因此在原来损失基础上加入一个项，就是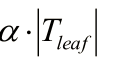，这个东西是一个系数乘以叶子的数量，也就是如果叶子数量过多，损失函数就没办法小了，其实跟L2正则是一个意思（l2正则也是参数过多会是损失函数变大）。

2、确定下来alpha值之后，选择最小的那个剪枝，一直选择最小的一直剪，最后剪到只剩下根节点形成K棵树

3、用测试集对K个树进行评价选择最好的树