线性回归

 一、线性回归

 

1、基本形式

其中：W表示了各个属性在变量中的权重

 

2、线性回归求解

损失函数的推导过程运用高斯分布+极大似然估计推导如下

所有样本满足这个公式：，其中e是误差项，假设满足高斯分布，可以写出概率分布函数如下

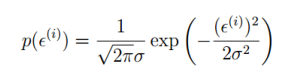，将e带入到概率分布函数中得到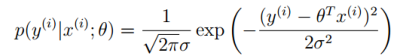

运用极大似然估计方法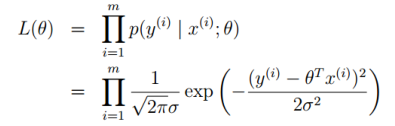，，然后取对数，得到对数似然估计

通过一系列数学运算，最后似然概率最大，也就是损失函数最小值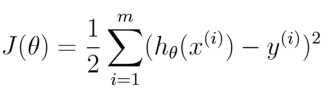这个取最小，也就是最小二乘法

损失函数：均方误差最小（最小二乘法），所以之所以可以用最小二乘法，是因为假定样本服从高斯分布。

也就是求损失函数最小值

 

求解的方法：分别对参数求导取得，写成矩阵形式时候可以将b写入w中，得到以下：

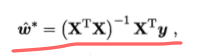
然而，现实中有时候，这个时候就无法求逆矩阵，比如有时候属性数目大于样本数，这时候就需要用到梯度下降算法来求参数w：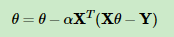

 

3、正则化

为了防止过拟合或者让不可逆的矩阵变成可逆，就需要在损失函数中引入正则化，防止参数过多导致曲线过于拟合，正则化对参数过多会有抑制的作用，参数过多会使得每个参数越来越大，因此如果加入平方项就可以抑制损失函数

最原始的是这样的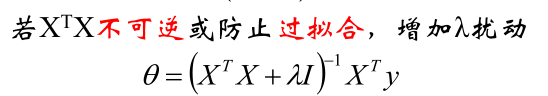

 

L1正则：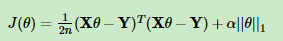

L2正则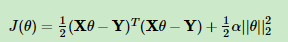：   这个加入的扰动项其实就是这么算的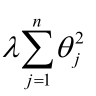，这是因为如果你的参数过大，那么就会让损失函数变大，那这个参数就不是最优解。

 

其中a为系数，需要通过调参来确定，由于L2正则是平方形式，因此对于参数的抑制更加强，这个式子说明，如果参数过多，损失函数会变大，并且如果参数过大，损失函数也会变大，损失函数变大，这个时候这个参数就不会选择

 

 

4、线性回归的变形（广义线性模型）

对于Y同样可以做变化，让x在原来线性模型基础上再套一个函数，输出到非线性空间中

 

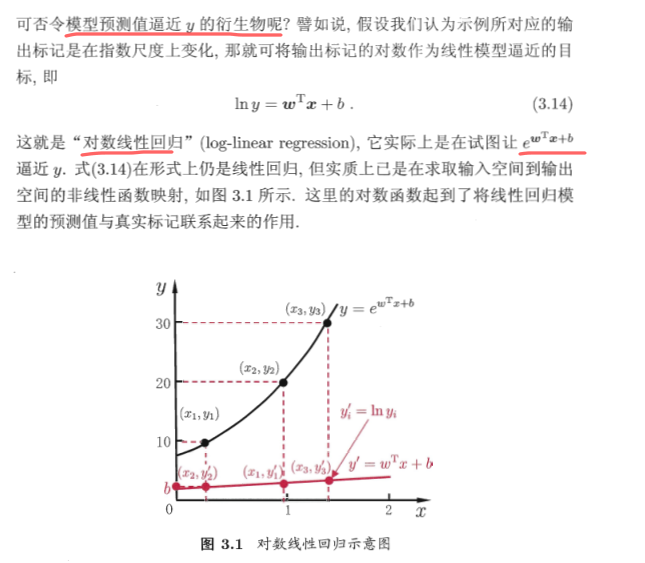
 把这种形式推广到一般的形式

 

二、Logistic回归

由于线性回归用于连续值的预测，若是二分类问题，则需要引入嵌套函数，将连续值映射到0,1，这里引入sigmoid函数

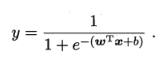，sigmoid函数的导数很有特点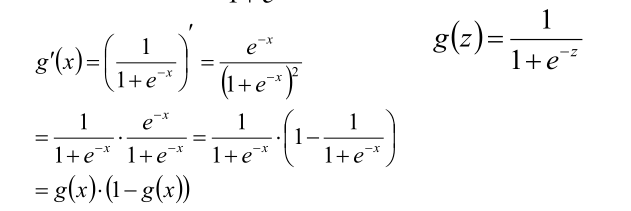

 

对于logistic回归的参数估计方法如下：

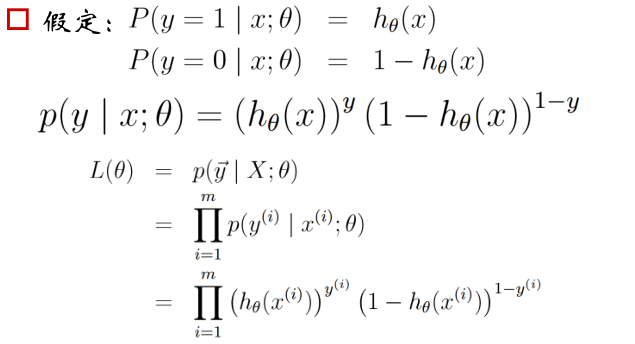这里将方程联立，并写出他们的联合分布（这里可以使用直接相乘的原因是因为假设他们独立），在使用极大似然估计方法估计参数

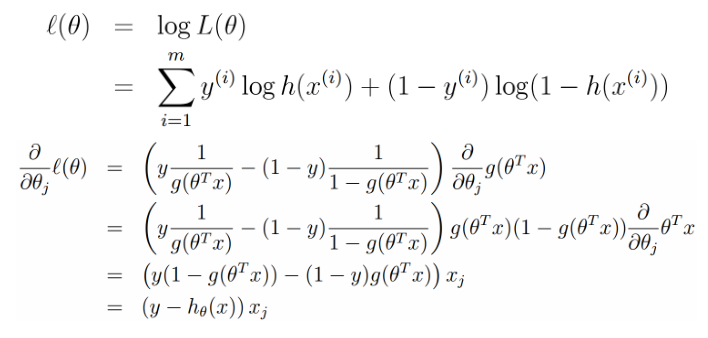，运用前面sigmoid函数导数特殊性来最后求得极大似然概率，

似然概率取最大值也就是损失函数取最小值，所以损失函数是似然概率的相反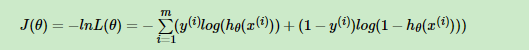

所以这个时候使用梯度下降算法是这样的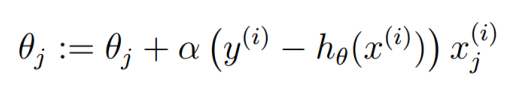或者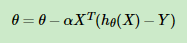，这两个其实一样，理解一下这里

 

 

三、损失的度量

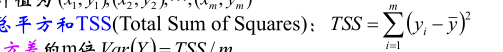这个是总平方和，也就是伪方差，与方差只差m倍

这个是残差平方和，也就是e，实际值与预测值的差异，这个值越小越好，但是由于样本本身有方差也就是tss，所以两个比值越小越好，R方越大越好

 混淆矩阵

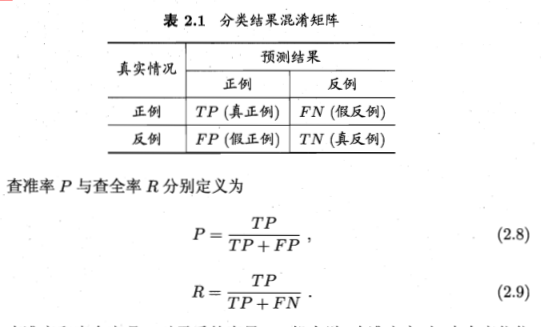
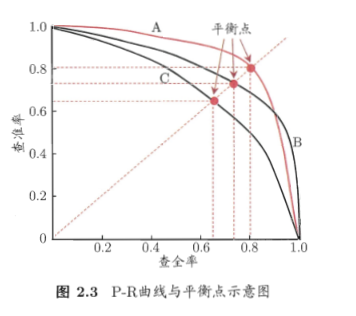
查全率：其实就是所有正例中有多少被预测到了    ；查准率：就是预测结果中正例中有多少是真的正例，一个基于预测结果，一个基于真实情况