各种奇妙姿势

gcd( Fib[n] , Fib[m] ) = Fib[ gcd(n,m) ]

 

任何一个数字都可以表示为斐波那契数列，贪心表示即可（从大到小）

 

对于n个(0,1)之间的随机变量x1..xn ，第k小的那个的期望值是 k / (n+1)

• 证明：
• 对于n个(0,1)之间的随机变量x1..xn ，第k小的那个的期望值是多少，这个问题可以转化为已经取了n个随机变量x1..xn之后，取第Xn+1个，问这一个<=第k个的概率（在这n+1个中排名<=k）
• 为什么可有这样转化呢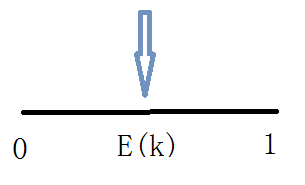：如左图，假如第k小的那个的期望值在坐标轴上是E(k)，那么根据几何概型，在该坐标轴上随便取一个值，该值<=E(K)的概率就是E(k)
• 转化后的问题（已经取了n个随机变量x1..xn之后，取第Xn+1个，问这一个<=第k个的概率）就好做多了，如下
• 考虑这n+1个随机变量的全排列，第Xn+1个在排列中从左到右数<=k的情况：先不看第Xn+1个，把其他n个排好共有 n! 种方案，再把第Xn+1个插进去，有k种插法，所以共有 k * ( n! ) 种方案，而n+1个随机变量全排列有 (n+1)! 个
• 所以答案为
  • \begin{equation*} \ \frac{k\ *\ ( \ n!\ )}{( \ n+1\ ) !} \end{equation*} \begin{equation*} \end{equation*} $ $$ $ \begin{multline*} \end{multline*}
• 然后约个分就是  k / (n+1) 了

 从n个数中取m个数（可重复）有多少种取法

• 假设这n个数为a[1]~a[n]，第i个数取c[i]个，则有$\sum_{i=1}^nc[i]=m$
• 相当于把m个球分到n个盒子里，盒子可以为空：把每个盒子里都放一个另外的球，就变成了把n+m个球分到n个盒子里，不为空
• 然后就是经典的插板法拉
• 所以有$C_{n+m-1}^{n-1}$种取法