辣些数论的思维题（枯了）

BZOJ 2659 算不出的算式

  • 关键是要想到这两个式子的几何意义。
  • 然后如图，以p1=5,p2=3为例子，整个矩形一定是被均分了的。
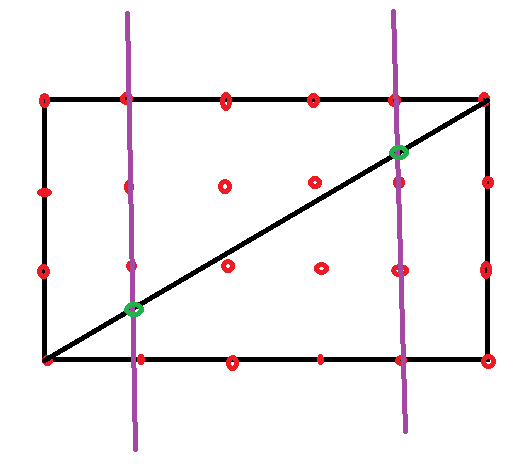
  • 如上图，单看每一列，绿点把红点分为上下两部分，绿点的位置又是中心对称的，所以整个红点（除了在对角线上的）都被等分到上三角和下三角了。
  • 由于p,q都是质数所以对角线上是不会有整点哒
  • 当p，q相等时，式子变成[1/p] + [2/p] + ... + [ ((p-1)/2) /p ]
  • 由 [ (x+n*p) / p ] =n   (x<p)  可知上面的是个有规律的数列。
  • 代码：
  •  1 #include <bits/stdc++.h>
 2  
 3 using namespace std;
 4 typedef unsigned long long ull;
 5  
 6 int main(){
 7     ull p,q,ans;
 8     cin>>p>>q;
 9     if(p==q) {
10         ull k=(q-1)/2;  //1+...+k
11         ans=(1+k)*k/2;
12         cout<<ans*2<<endl;
13         return 0;
14     }
15     ans=(p+1)*(q+1)/4;
16     ans-=((p+1)/2+(q+1)/2);
17     cout<<ans+1<<endl;
18     return 0;
19 }
20
    quq

     

洛谷P3951 NOIP2017 小凯的疑惑

  • 倒回去看那年的题，所以为什么会爆0，三十分都没有啊(╯‵□′)╯︵┻━┻
  • 拿三和五为例子，考虑数轴
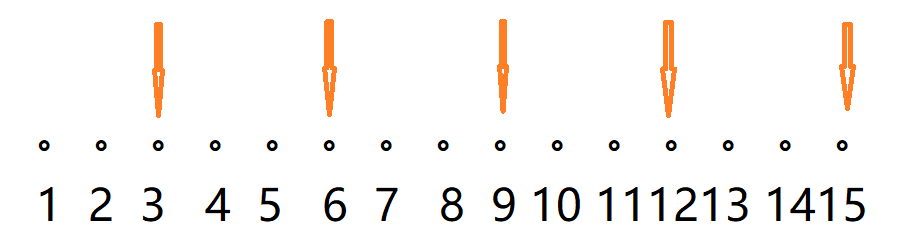
  • 这些是三的倍数能指着的点，可以看出所有的数里每三个数就有一个能被表示。
  • 现在看加上5的情况
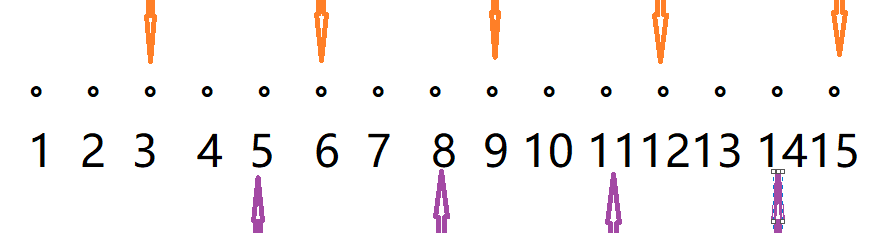
  • 这里由于第一个5在三的后面两位，一直倍数下去，这样所有的数每三个数就有两个能被表示
  • 而第二个5，就是10正好踩到后面一位，这样这之后的每三个数的这一位一定能被表示
  • 这样就能表示完那后面所有的数了。
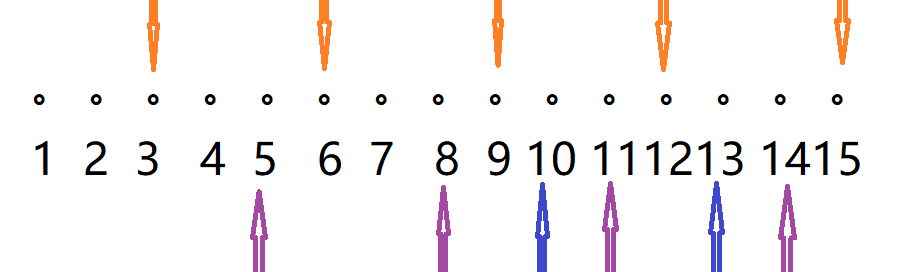
  • 所以任意两个p,q（互质）的情况是一样的，不妨假设p<q
  • q%p
  • 2*q%p
  • 3*q%p
  • ......
  • （p-1）*q%p
  • 可以知道上面这些的结果一定都不一样，（如果一样，那就一定有p是q的因数，这与他俩互质矛盾）
  • 所以在p*q之前q之间的空挡一定被q踩完，这之后的任意数都能被表示
  • 那第一个不能被表示的数呢？
  • 我们知道最后一个被踩的空挡是(p*q)-q，在这个空档之前的这个空挡都是踩不到的，所以就在它前一个就是最大的无法表示的数了，即为p*q-p-q
  • 代码： 
     1 #include <bits/stdc++.h>
 2 
 3 using namespace std;
 4 typedef long long ll;
 5 
 6 int main(){
 7     ll a,b; //a>b
 8     cin>>a>>b;
 9     cout<<(a*b)-a-b<<endl;
10     return 0;
11 }
    嘤击长空

BZOJ1008: [HNOI2008]越狱

  • 考虑不发生越狱的情况，m* ( m-1 )^(n-1)
  • 全部情况：m^n
  • 快速幂
  • 代码： 
     1 #include <bits/stdc++.h>
 2 #define mod 100003
 3  
 4 using namespace std;
 5 typedef long long ll;
 6 ll m,n;
 7  
 8 ll exp(ll x,ll v){
 9     if(x==1) return v;
10     ll t=exp(x/2,v);
11     t=(t*t)%mod;
12     return (x%2) ? (t*v)%mod : t;
13 }
14  
15 int main(){
16     cin>>m>>n;
17     ll a=exp(n,m),b=exp(n-1,m-1);
18     ll ans=a-(m*b)%mod;
19     if(ans<0) ans+=mod;
20     cout<<ans<<endl;
21     return 0;
22 }
    嘤帝质疑

 

BZOJ2818: Gcd

  • 题意：给定整数N，求1<=x,y<=N且Gcd(x,y)为素数的
    数对(x,y)有多少对.    其中1<=N<=10^7
  • 欧拉函数
  • 先枚举gcd(x,y)的值，然后再求所有这些数中有枚举的这个数的因子的数中互质的对数，后者用欧拉函数再求一个前缀和就ok了
  • 代码（注意欧拉函数求前缀和到后面会爆int，要开long long才行） 
     1 #include <bits/stdc++.h>
 2  
 3 using namespace std;
 4 typedef long long ll;
 5 ll phi[10000005];
 6 int pri[10000005],table[10000005]={0};
 7 int cp=-1,n;
 8 ll ans=0;
 9  
10 void getphi(){
11     for (int i=2; i<=1e7; i++) {
12         if(!table[i]) { pri[++cp]=i; phi[i]=i-1; }
13         for (int j=0; j<=cp; j++){
14             ll t=pri[j]*i;
15             if(t>1e7) break;
16             table[t]=1;
17             if(i%pri[j]==0) { phi[t]=phi[i]*pri[j]; break;}
18             phi[t]=phi[i]*(pri[j]-1);
19         }
20     }
21 }
22  
23 int main(){
24     getphi();
25     for (int i=1; i<=1e7; i++) phi[i]+=phi[i-1];
26     cin>>n;
27     for (int i=0; i<=cp; i++) {
28         if(n<pri[i]) break;
29         ans+= (phi[ n/pri[i] ]<<1) ;
30         ans++;
31     }
32     cout<<ans<<endl;
33     return 0;
34 }
    嘤雄不朽

 

 

BZOJ2705: [SDOI2012]Longge的问题

  • 题意： 给定一个整数N，你需要求出∑gcd(i, N)(1<=i <=N)   其中0<N<=2^32。

  • 这个题没做出来主要是因为没考虑过枚举N的因数（其实是因为我人傻）
  • 对啊根号N就可以枚举N的所有因数了何必想的辣么复杂呢
  • 代码： 
     1 #include <bits/stdc++.h>
 2  
 3 using namespace std;
 4 typedef long long ll;
 5  
 6 ll phi(ll x){
 7     ll sqx=sqrt(x),tx=x;
 8     for (ll i=2; i<=sqx; i++) {
 9         if(tx%i) continue;
10         x/=i;
11         x*=(i-1);
12         while(tx%i==0) tx/=i;
13         if(tx==1) break;
14     }
15     if(tx>1) { x/=tx; x*=(tx-1); }
16     return x;
17 }
18  
19 int main(){
20     ll ans=0,n;
21     cin>>n;
22     ll m=sqrt(n);
23     for (int i=2; i<=m; i++) {
24         if(n%i) continue;
25         ans+=phi(n/i)*i;
26         if(i*i<n) ans+=(n/i)*phi(i);
27     }
28     ans+=(n+phi(n));
29     cout<<ans<<endl;
30     return 0;
31 }
    满门嘤烈

 

 

BZOJ1045: [HAOI2008] 糖果传递

  • 有n个小朋友坐成一圈，每人有ai个糖果。每人只能给左右两人传递糖果。每人每次传递一个糖果代价为1。
  • 假设第x(i)个人给了第x(i+1)个人b个糖果，然后如果一个人接到的糖果是n+b的话，算一下最后每个人的糖果数就可以知道它拿出去的也是一个整数加b的形式，那最后要求的ans=min对abs(n+b)求和;b是唯一的变量，n是可以算出来的整数
  • 于是就转化成了一种常见模型：求数轴上n个点到哪一点距离之和最短。。。
  • 代码： 
     1 #include <cstdio>
 2 #include <iostream>
 3 #include <algorithm>
 4 #define nmax 1000010
 5  
 6 using namespace std;
 7 typedef long long ll;
 8 int c[nmax],b[nmax]={0};
 9 ll tot=0,a=0;
10 int n;
11  
12 ll cntdis(ll x){
13     ll d=0;
14     for (int i=0; i<n; i++) d+=abs(b[i]-x);
15     return d;
16 }
17  
18 int main(){
19     cin>>n;
20     for (int i=0; i<n; i++) {
21         scanf("%d",&c[i]);
22         tot+=c[i];
23     }
24     a=tot/n;
25     for (int i=1; i<n; i++) b[i]=b[i-1]-a+c[i];
26     for (int i=1; i<n; i++) b[i]*=(-1);
27     sort(b,b+n);
28     if(n&1) cout<<cntdis(b[n/2])<<endl;
29     else cout<<cntdis(b[n/2-1])<<endl;
30     return 0;
31 }
    嘤姿勃发

     

posted @ 2019-08-12 20:06  连昵称都不能重复  阅读(201)  评论(0)  编辑  收藏  举报