水比的 树状数组 刷题记录

洛谷P3374 【模板】树状数组 1

  • 单点修改，区间查值。细节看代码
  • 代码：
 1 #include <bits/stdc++.h>
 2 #define nmax 500010
 3 
 4 using namespace std;
 5 int n,m;
 6 int a[nmax],qz[nmax]={0},c[nmax];
 7 
 8 inline int lowb(int x){ return x&(-x); }
 9 
10 void build(){
11     cin>>n>>m;
12     for (int i=1; i<=n; i++) {
13         scanf("%d",&a[i]);
14         qz[i]=qz[i-1]+a[i];
15         c[i]=qz[i]-qz[i-lowb(i)];
16     }
17 }
18 
19 inline void add(int x,int k){
20     a[x]+=k;      //这里x+=lowb(x)是走向它父亲节点所以先加后走，判断时是x<=n
21     while(x<=n) {  c[x]+=k; x+=lowb(x); }
22 }
23 
24 inline int findqz(int x){  //求1~x的和
25     int ans=0;
26     while(x) { ans+=c[x]; x-=lowb(x);   }
27     return ans;
28 }
29 
30 inline int query(int x,int y) { return findqz(y)-findqz(x-1); }
31 
32 int main(){
33     build();
34     int b,x,y;
35     for (int i=0; i<m; i++) {
36         scanf("%d%d%d",&b,&x,&y);
37         if(b==1)  add(x,y);
38         else printf("%d\n",query(x,y));
39     }
40     return 0;
41 }
  • 写树状数组的感觉比写线段树的感觉好多了~在家里一个人打线段树好无聊，都没有朋友玩，没有女仔玩。打了树状数组发现个个都是位运算，行数又少，超喜欢树状数组的。

洛谷P3368 【模板】树状数组 2

  • 区间修改（区间加），单点查值。
  • 代码： 
     1 #include <bits/stdc++.h>
 2 #define nmax 500010
 3 
 4 using namespace std;
 5 int n,m;
 6 int a[nmax],c[nmax]={0};
 7 
 8 inline int lowb(int x){ return x&(-x); }
 9 
10 inline void ta(int x,int k){  //把1~x的c[i]都加上k
11     while(x) { c[x]+=k; x-=lowb(x);   }
12 }
13 
14 inline void add(int x,int y,int k){
15     ta(x-1,-k);
16     ta(y,k);
17 }
18 
19 inline int query(int x) {
20     int tot=a[x];  //得在x还没有变的时候把a[x]给加上
21     while(x<=n) {  tot+=c[x]; x+=lowb(x); }
22     return tot;
23 }
24 
25 int main(){
26     cin>>n>>m;
27     for (int i=1; i<=n; i++) scanf("%d",&a[i]);
28     int b,x,y,k;
29     for (int i=0; i<m; i++) {
30         scanf("%d",&b);
31         if(b==1) {
32                 scanf("%d%d%d",&x,&y,&k);
33                 add(x,y,k);
34         }
35         else { scanf("%d",&x); printf("%d\n",query(x)); }
36     }
37     return 0;
38 }
    View Code

     

 BZOJ 1106: [POI2007]立方体大作战tet

  • 思路：拿例子 5 2 3 1 4 1 4 3 5 2来说

                     看某一段例如   5 2 3 1 4 1 4 3 5这段，我肯定不先消去55，因为55中间有11，44，33没消，如果划去55，消去11，44，33的代价不变，但是划去11，44，33的话，消去55的代价就变低了，所以对于连个相同的数中间还有相同的数的情况，先把中间相同的数删去。

                    剩下的一串数就是中间没有相同的数了，拿样例二来说1 2 3 1 2 3，考虑这样一种策略，我第二次走到这个数时，我移动并删去它。

                    走到i=4了，删去11，移动两次，数组变成 2 3 2 3，继续向后走到2，变成 3 3，最后删去 3 3.

                    也就是说，光看策略的话，是一直删去的那些中间没有相同的数的数，直到删完，拿例子一来说：

                   开始5 2 3 1 4 1 4 3 5 2

                          5 2 3 4 4 3 5 2

                          5 2 3 3 5 2

                          5 2 5 2

                          2 2         结束

  • 怎么用树状数组维护？

                   不看第二次出现的数，只统计区间内第一次出现的数的个数，然后挨个删去并统计代价即可。

                   单点修改，区间查值。

  • 代码：
 1 #include <bits/stdc++.h>
 2 #define nmax 50010
 3 #define lowbit(x) (x&(-x))
 4 //单点修改，区间查值
 5 using namespace std;
 6 int n;
 7 int a[nmax*2],id[nmax*2]={0},c[nmax*2]={0};//id -> 记录第一次出现的坐标
 8 //c -> 区间内不同的数的个数
 9 inline void add(int j,int k){
10     while(j<=n) { c[j]+=k; j+=lowbit(j); }
11 }
12 
13 void build(){
14     cin>>n;
15     n*=2;
16     for (int i=1; i<=n; i++) {
17         scanf("%d",&a[i]);
18         int& t=id[a[i]];
19         if( !t ) {  t=i; add(i,1); } //第一次出现
20     }
21 }
22 
23 inline int tf(int x) {
24     int ans=0;
25     while(x>=1){ ans+=c[x]; x-=lowbit(x); }
26     return ans;
27 }
28 //找x~y中间不同且第一次出现的数
29 int myfind(int x,int y){ return tf(y-1)-tf(x); }
30 
31 int main(){
32     build();
33     int ans=0;
34     for (int i=1; i<=n; i++) {
35         int t=id[a[i]];
36         if(t!=i) {
37             ans+=myfind(t,i);
38             add(t,-1);
39         }
40     }
41     cout<<ans<<endl;
42     return 0;
43 }
点人家看代码030

 

 BZOJ3155: Preprefix sum

  • 题意：单点修改，然后区间查询前缀和的前缀和
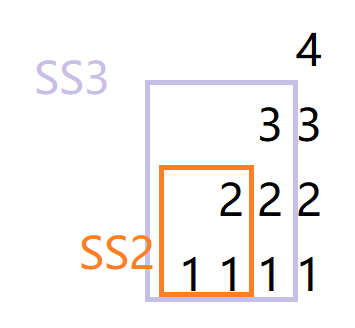  • 从右面看SS2就等于四个一和三个2减去2倍的S2（S是前缀和）,然后考虑维护两个树状数组
  • 代码（注意loong long) 
     1 #include <bits/stdc++.h>
 2 #define nmax 100010
 3 #define lowbit(x) (x&(-x))
 4  
 5 using namespace std;
 6 typedef long long ll;
 7 ll a[nmax][3]={0},c[nmax][3]={0},qz[nmax][3]={0};//两个单点修改，区间查值
 8 int n,m;
 9  
10 void build(){
11     scanf("%d%d",&n,&m);
12     for (int i=1; i<=n; i++) {
13         scanf("%lld",&a[i][1]);//1是前缀和，2是前缀和的前缀和
14         a[i][2]=a[i][1]*(n-i+1);
15         qz[i][1]=a[i][1]+qz[i-1][1];
16         qz[i][2]=a[i][2]+qz[i-1][2];
17         c[i][1]=qz[i][1]-qz[i-lowbit(i)][1];
18         c[i][2]=qz[i][2]-qz[i-lowbit(i)][2];
19     }
20 }
21  
22 inline void add(int x,ll k,int id){ //给x加上k
23     while(x<=n){ c[x][id]+=k; x+=lowbit(x); }
24 }
25  
26 inline ll query(int x){  //SSx的值
27     ll ans=0,ta=0;
28     int k=x;//到后面已经改变了，到底多少次才会记住拉
29     while(x>0) {
30         ans+=c[x][2];
31         ta+=c[x][1];
32         x-=lowbit(x);
33     }
34     ans-=(ta*(n-k));
35     return ans;
36 }
37  
38 int main(){
39     build();
40     char in[20];
41     int x,y;
42     while(m--){
43         scanf("%s",in);
44         if(in[0]=='Q'){
45             scanf("%d",&x);
46             printf("%lld\n",query(x));
47         }else{
48             scanf("%d%d",&x,&y);
49             ll ta=y-a[x][1];
50             a[x][1]=y;
51             add(x,ta,1);
52             add(x,ta*(n-x+1),2);
53         }
54     }
55     return 0;
56 }
    φ(≧ω≦*)♪

     

HDU1541 Stars

  • 二维偏序，用的树状数组
  • xy已经排好序所以只看x，y[i-1]~y[1]的一定是小于y[i]的，只要统计x[i-1]~x[1]中小于x[i]的个数就行
  • 用结构体排序，c[i]表示当前x[1]~x[i]的个数，每次找到排序后最大的辣个x的下标id，查找c[id]，然后删除x[id]
  • 区间查值，单点修改
  • 代码：（坑点众多，一定要看discuss  quq) 
     1 #include <bits/stdc++.h>
 2 #define nmax 15010
 3 #define lowbit(x) (x&(-x))
 4 
 5 using namespace std;
 6 typedef long long ll;
 7 int n,y;
 8 int x[nmax],c[nmax],an[nmax]={0};
 9 struct point{
10     int x,id;
11     bool operator < (const point a) const{
12         return (a.x==x)?(a.id<id):(a.x<x);
13     }
14 }p[nmax];
15 
16 inline int query(int x){
17     int ans=0;
18     while(x>0) { ans+=c[x]; x-=lowbit(x); }
19     return ans;
20 }
21 
22 inline void del(int x){
23     while(x<=n){ c[x]--; x+=lowbit(x); }
24 }
25 
26 int main(){
27     while(scanf("%d",&n)!=EOF){
28         memset(an,0,sizeof(an));
29         for (int i=1; i<=n; i++) {
30                 scanf("%d%d",&x[i],&y);
31                 p[i].x=x[i];
32                 p[i].id=i;
33                 c[i]=lowbit(i);
34         }
35         sort(p+1,p+1+n);
36         for (int i=1; i<=n; i++) {
37             int t=query(p[i].id)-1;
38             an[t]++;
39             del(p[i].id);
40         }
41         for (int i=0; i<n; i++) printf("%d\n",an[i]);
42     }
43     return 0;
44 }
    (；′⌒`)

 

HDU 1394Minimum Inversion Number

  • 一定要把题意看清了再做题！！！
  • hud上做题一定要多组数据输入输出！！！
  • 考虑最前面的那个数，它后面大于和小于它的数已知，则把它移到最后所增加的逆序对数可以O（1）求出
  • 代码：while(scanf("%d",&n))会tle。。。一定要加EOF 
     1 #include <bits/stdc++.h>
 2 #define nmax 5010
 3 #define lowbit(x) x&(-x)
 4 #define inf 1e9
 5 
 6 using namespace std;
 7 int n;
 8 int a[nmax],c[nmax]={0};
 9 
10 void madd(int p){
11     while(p<=n){ c[p]++; p+=lowbit(p); }
12 }
13 
14 int mfind(int p){
15     int ans=0;
16     while(p>0) { ans+=c[p]; p-=lowbit(p); }
17     return ans;
18 }
19 
20 int main(){
21     //freopen("owo.txt","r",stdin);
22     while(scanf("%d",&n)!=EOF){
23         for (int i=1; i<=n; i++) {
24             scanf("%d",&a[i]);
25             a[i]++;
26             c[i]=0;    
27         }
28         int ta=0,t,tp,ans=inf;
29         //找逆序对
30         for (int i=1; i<=n; i++){
31             t=mfind(a[i]);
32             ta+=(i-t-1);
33             madd(a[i]);
34         }
35         for (int i=1; i<=n; i++) {
36             ta+=(n-a[i]);
37             ta-=(a[i]-1);
38             ans=min(ans,ta);
39         }
40         cout<<ans<<endl;
41     }
42     return 0;
43 }
    (╯‵□′)╯︵┻━┻

     

posted @ 2019-07-31 23:23  连昵称都不能重复  阅读(150)  评论(0)  编辑  收藏  举报