【CV论文阅读】生成式对抗网络GAN

生成式对抗网络GAN

1、  基本GAN

在论文《Generative Adversarial Nets》提出的GAN是最原始的框架，可以看成极大极小博弈的过程，因此称为“对抗网络”。一般包含两个部分：生成器（Generator）和判别器（Discriminator）。训练的过程是无监督学习。

先总结一下训练的过程。一般而言，输入是一个一维向量z，它从先验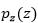生成。假设现在Generator生成的是图像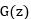。我们知道，无监督学习目的是学习数据集中的特征（或者说分布），假设真实的分布为，而Generator的生成图像的过程其实隐式地定义了一个学习到的分布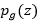。把生成的图像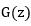输入到Discriminator中即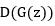，计算的是样本来自于真实分布而不是由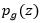生成的概率，因为Discriminator最终只有一个输出。上述无论是Generator或者Discriminator都是一般常见的网络，如下图：

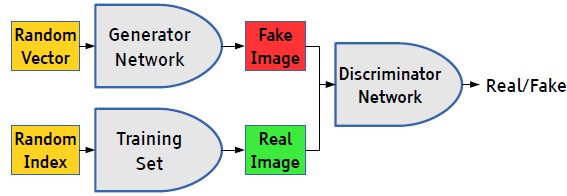
如上所说，训练的过程是极大极小的博弈过程，归纳成下式：

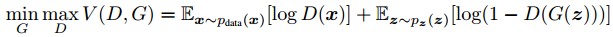
即Generator希望极大化Discriminator误判的概率，而Discriminator极小化把生成样本判成来自真实data的概率。论文中证明，上式的最优解在于。

可以看到，学习到的样本分布（或者特征表示）并没有一个显式的结果，这算是GAN的一个缺点了。训练的过程是同时训练两个网络，由于Discriminator可以更好地指导Generator的调整，所以一般会让Discriminator循环的次数更多。最优化过程使用的是梯度下降算法，如下：

疑惑：在训练D的时候，按照公式应该是一个极大化的过程，为什么可以使用SGD呢？因此我觉得上式应该是不对的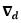，之前应该缺少一个负号转换成一个极小化的问题。

而开始时，可能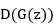会很接近于0，这使得log函数也接近于0，最终结果是梯度下降时由于回流梯度过小无法更新浅层网络。因此，论文建议训练开始时可以求解极大化。

 

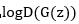2、深度卷积生成对抗网络DCGAN

论文《UNSUPERVISED REPRESENTATION L EARNING WITH DEEP CONVOLUTIONAL GENERATIVE ADVERSARIAL NETWORKS》提出DCGAN，可以看成是GAN应用在CNN的尝试。论文更多的是在CNN工程上的尝试经验，由于GAN在训练时的不稳定性，因此提出了几点改变：

1、把所有的pooling层用strided convolution替代。在D网络即是跨步长的卷积，在G网络则是上采样（此处称为fractional-strided，但很多代码实现似乎都用了deconv，在tensorflow有这样一个函数）。

2、在G和D都应用BN，但是在G的输出层和D的输入层不应用BN。

3、移除全连接层

4、在G中的激活函数使用RELU，但在输出层使用的是Tanh

5、在D中的激活函数全部使用Leaky ReLu。

结构图如下：

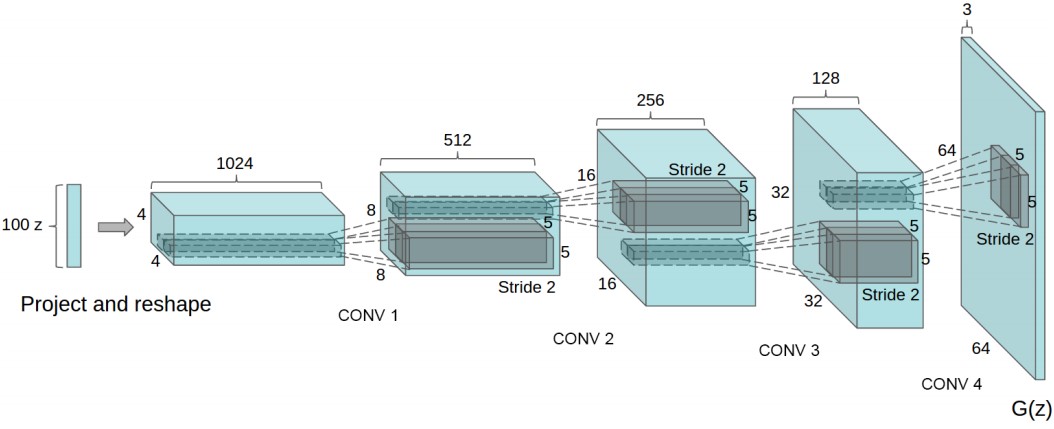
这里主要看它的实现过程。代码来自https://github.com/carpedm20/DCGAN-tensorflow/blob/master/model.py 。

D网络部分和一般的卷积网络没有什么区别，主要最后一步是把feature map进行一个flatten的操作，然后全部feed到一个sigmoid的单元，即下式的h4。

  h0 = lrelu(conv2d(image, self.df_dim, name='d_h0_conv'))
  h1 = lrelu(self.d_bn1(conv2d(h0, self.df_dim*2, name='d_h1_conv')))
  h2 = lrelu(self.d_bn2(conv2d(h1, self.df_dim*4, name='d_h2_conv')))
  h3 = lrelu(self.d_bn3(conv2d(h2, self.df_dim*8, name='d_h3_conv')))
  h4 = linear(tf.reshape(h3, [self.batch_size, -1]), 1, 'd_h3_lin')
  return tf.nn.sigmoid(h4), h4

　　

注意这里的conv2d实现时已经加上了bias。

在G网络部分，主要关注z到project and reshape部分和如何进行fractional-strided convolution。

对于project and reshape，代码中的实现是：

self.z_, self.h0_w, self.h0_b = linear(z, self.gf_dim*8*s16*s16, 'g_h0_lin', with_w=True)
self.h0 = tf.reshape(self.z_, [-1, s16, s16, self.gf_dim * 8])

　　

其中linear（）函数是通过matrix相乘把z变成self.gf_dim*8*s16*s16 大小的向量。然后通过reshape得到feature maps。

而对于fractional-strided convolution，这里使用一个函数deconv2d（），代码如下：

w = tf.get_variable('w', [k_h, k_w, output_shape[-1], input_.get_shape()[-1]],initializer=tf.random_normal_initializer(stddev=stddev))
deconv = tf.nn.conv2d_transpose(input_, w, output_shape=output_shape, strides=[1, d_h, d_w, 1])
biases = tf.get_variable('biases', [output_shape[-1]], initializer=tf.constant_initializer(0.0))
deconv = tf.reshape(tf.nn.bias_add(deconv, biases), deconv.get_shape())

　　

通过一个tf.nn.conv2d_transpose（）函数实现反卷积。但有一点注意的是，tf.nn.conv2d_transpose（）函数不是什么shape都可以输出的，验证是否正确的方法是，把output与卷积核w做一次卷积，如果得到的shape和input的一致，代表是正确的。

可以参考http://stackoverflow.com/questions/35488717/confused-about-conv2d-transpose 。

 

3、条件GAN conditional GAN

条件GAN，我认为很多blog是写错了的，它和条件概率应该是没有关系的。GAN的一个很大的优点是，它的输入很灵活没有过大的限制。而条件GAN其实是在一般输入时添加了额外的input，这作为一个可控制的变量去指导着网络的训练。因为基本GAN的训练应该是无方向（这里表达不准确）的。

一个简单的网络如下：

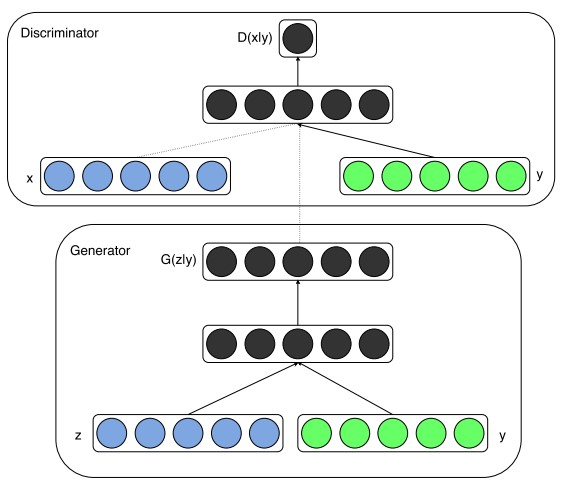
Y作为额外的输入的变量，是可控的。在论文《Conditional Generative Adversarial Nets》中的一个例子是训练mnist，其中y则是0~9的标签的一个one-hot的编码向量。

此外，由于GAN输入的灵活，可以很容易想到可以加入多模态的信息对网络训练进行指导，事实上已经有了不少的尝试。