多米诺牌集
多米诺gu牌覆盖问题也是经典的题目了,主要是由1*k的牌覆盖m*n的矩阵之类的。有递推求解的,也有的如下:
如POJ 2411,由1*2的小矩形去覆盖m*n的矩形,问有多少种方案。
这道题其实只要计算出上下两行之前的可能存在的状态转换,这样就很容易求解了。如下:
void dfs(int pre,int now,int l){//上一行的状态,当前行的状态,当前列的位置
if(l>w) return;
if(l==w){
trans[nt][0]=pre,trans[nt++][1]=now;
return ;
}
dfs(pre<<1,now<<1|1,l+1); //竖着放,则上一行当前为置为空,下一行被覆盖
dfs(pre<<2|3,now<<2|3,l+2);//当前行横着放
dfs(pre<<1|1,now<<1,l+1);//当前行当前位置不放
}
于是,POJ 2411 可以如下解题:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define LL __int64
using namespace std;
int nt,h,w;
int trans[11*(1<<11)][2];
LL f[12][1<<11];
void dfs(int pre,int now,int l){
if(l>w) return;
if(l==w){
trans[nt][0]=pre,trans[nt++][1]=now;
return ;
}
dfs(pre<<1,now<<1|1,l+1);
dfs(pre<<2|3,now<<2|3,l+2);
dfs(pre<<1|1,now<<1,l+1);
}
int main(){
while(scanf("%d%d",&h,&w),h||w){
nt=0;
dfs(0,0,0);
memset(f,0,sizeof(f));
f[0][(1<<w)-1]=1;
for(int i=1;i<=h;i++){
for(int j=0;j<nt;j++){
if(f[i-1][trans[j][0]]){
f[i][trans[j][1]]+=f[i-1][trans[j][0]];
}
}
}
printf("%I64d\n",f[h][(1<<w)-1]);
}
return 0;
}
另外如POJ 2663,也是同样的解法。
#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #define LL __int64 using namespace std; int trans[10*(1<<3)][2]; int nt; //LL dp[2001][20001]; LL f[31][1<<3]; void dfs(int pre,int now,int l){ if(l>3) return ; if(l==3){ trans[nt][0]=pre; trans[nt++][1]=now; return ; } dfs(pre<<1,now<<1|1,l+1); dfs(pre<<2|3,now<<2|3,l+2); dfs(pre<<1|1,now<<1,l+1); } int main(){ int n; nt=0; dfs(0,0,0); while(~scanf("%d",&n)){ if(n==-1) break; memset(f,0,sizeof(f)); f[0][(1<<3)-1]=1; for(int i=1;i<=n;i++){ for(int j=0;j<nt;j++){ if(f[i-1][trans[j][0]]){ f[i][trans[j][1]]+=f[i-1][trans[j][0]]; } } } printf("%I64d\n",f[n][(1<<3)-1]); } return 0; }
POJ 3420.由于n比较大,而且两行之间的状态转换就是不断的重复,可以使用快速矩阵乘法,把状态转换矩阵保存下来,然后快速乘,则结果保存在trans[15][15]的位置。
#include <iostream> #include <cstdio> #include <cstring> using namespace std; struct Matrix{ int trans[1<<4][1<<4]; void init(){ memset(trans,0,sizeof(trans)); } void per(){ memset(trans,0,sizeof(trans)); for(int i=0;i<16;i++) trans[i][i]=1; } }; int M,n; Matrix T; Matrix multi(Matrix a,Matrix b){ Matrix ans; ans.init(); for(int i=0;i<16;i++){ for(int j=0;j<16;j++){ for(int k=0;k<16;k++){ ans.trans[i][j]=(ans.trans[i][j]+(a.trans[i][k]*b.trans[k][j])%M)%M; } } } return ans; } void dfs(int pre,int now,int l){ if(l>4) return ; if(l==4){ T.trans[pre][now]++; return ; } dfs(pre<<1|1,now<<1,l+1); dfs(pre<<2|3,now<<2|3,l+2); dfs(pre<<1,now<<1|1,l+1); } int quick(int n){ Matrix p; p.per(); Matrix sq=T; while(n){ if(n&1) p=multi(sq,p); sq=multi(sq,sq); n>>=1; } return p.trans[15][15]; } int main(){ T.init(); dfs(0,0,0); while(scanf("%d%d",&n,&M),n||M){ printf("%d\n",quick(n)); } return 0; }
HDU 5100
问以1*k的小矩阵覆盖n*n的大矩形,最多能覆盖的面积。
对于n%k==0的情况就不用说了,对于不整除的,可以直观的发现,不覆盖的情况必定是个正方形,其边长要么是n%k或者k-n%k。其实这个是可以证明的,
转自http://www.matrix67.com/blog/archives/5900。。。。。。我没有侵权啊。。。T_T
用 k × 1 的小矩形覆盖一个 n × n 的正方形棋盘,往往不能实现完全覆盖(比如,有时候 n × n 甚至根本就不是 k 的整倍数)。不过,在众多覆盖方案中,总有一种覆盖方案会让没有覆盖到的方格个数达到最少,我们就用 m(n, k) 来表示这个数目。求证:不管 n 和 k 是多少, m(n, k) 一定是一个完全平方数。
如果 n < k ,那么很明显,棋盘里一个小矩形也放不下,因而 m(n, k) = n2 ,这是一个完全平方数。下面我们就只考虑 n ≥ k 了。
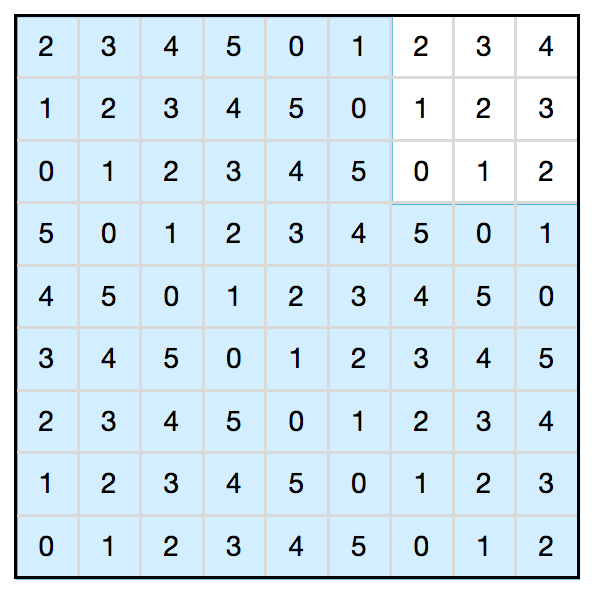
我们先来证明这样一个事实:如果某个覆盖方案当中,仅剩下一个 s × s 的小正方形区域没有覆盖到,其中 s ≤ k / 2 ,那么这样的方案一定是最优的。首先,在棋盘中的每个格子里都填上一个数,使得从最左下角出发,各个对角线上的数依次为 0, 1, 2, …, k – 1, 0, 1, 2, …, k – 1, … (上图所示的是 k = 6 的情况)。那么,把一个 k × 1 的小矩形放在棋盘中的任意位置,它总会覆盖每种数字各一个。假设某个覆盖方案当中,仅剩下一个 s × s 的小正方形区域没有覆盖到。注意到,任意一个 s × s 的小正方形区域里最多只会出现 2s – 1 种不同的数,因此如果 s ≤ k / 2 ,那么这个 s × s 的小正方形区域里一定会缺失至少一种数,比方说 x (在上图中,右上角的那个 3 × 3 的空白区域里就缺数字 5 ,因而我们可以取 x = 5 )。由此可以推出,此时小矩形的数目已经达到了最大值,任何其他覆盖方案都不可能包含更多的小矩形,因为每个小矩形都必然会覆盖到一个 x ,然而在刚才的覆盖方案中,所有的 x 都已经被覆盖到了。
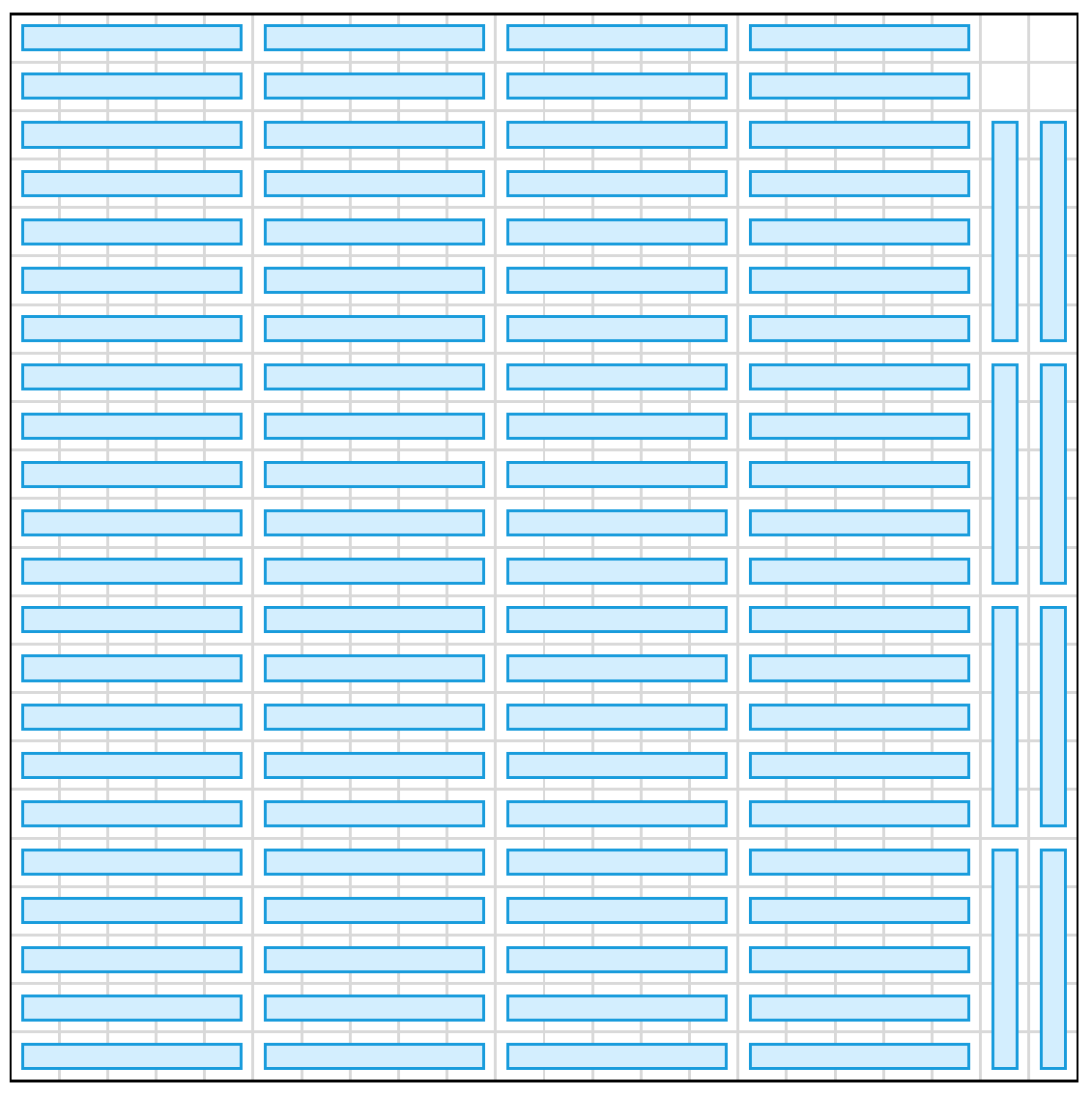
有趣的是,当 n ≥ k 时,让整个棋盘仅剩一个边长不超过 k / 2 的小正方形区域没有覆盖到,这是一定能做到的。不妨把 n 除以 k 的余数记作 r 。如果 r ≤ k / 2 ,那么我们可以直接用横着的小矩形从左向右填充棋盘,再用竖着的小矩形填充余下的部分,最终会剩下 r × r 的小正方形区域。上图所示的就是 n = 22 并且 k = 5 的情况,注意到 22 除以 5 的余数为 2 ,确实小于等于除数 5 的一半。可见,对于这类情况,我们都有 m(n, k) = r2 ,这是一个完全平方数。
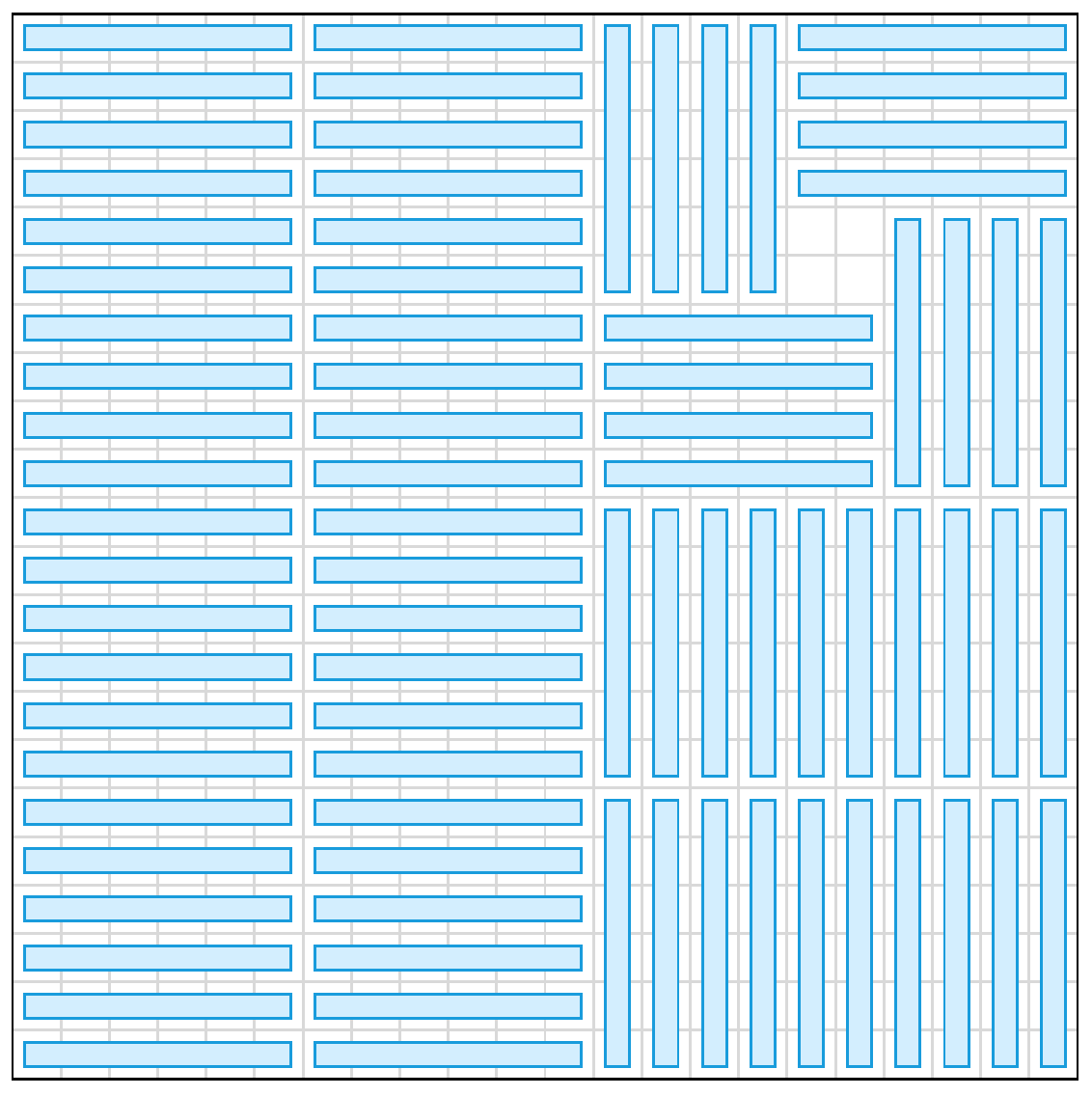
如果 r > k / 2 呢?我们可以用和刚才类似的方法填充棋盘,使得棋盘右上角仅剩一个 (r + k) × (r + k) 的正方形区域。然后再用 4r 个小矩形像风车一样填充这个 (r + k) × (r + k) 的区域,使得正中间只剩下一个边长为 k – r 的小正方形区域。由于 k – r < k / 2 ,因而此时的覆盖方案再次达到最优。上图所示的就是 n = 22 并且 k = 6 的情况,注意到 22 除以 6 的余数为 4 ,确实大于除数 6 的一半。可见,对于这类情况,我们有 m(n, k) = (k – r)2 ,这仍然是一个完全平方数。
HDU 5100
#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> using namespace std; int main(){ int n,k,T; scanf("%d",&T); while(T--){ scanf("%d%d",&n,&k); if(k>n){ puts("0"); continue; } if(n%k==0) printf("%d\n",n*n); else{ int l=min(n%k,k-n%k); printf("%d\n",n*n-l*l); } } return 0; }



