POJ 2008
这道题,说实话,细节很多。不过,我没想到,光细节就能搞死人了。。。
参考了http://www.cppblog.com/varg-vikernes/archive/2010/03/12/109559.html
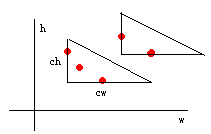
首先,要把所有牛放到坐标系上来表示。目的,就是求出包含最多点的直角三角形。
直角三角形的两条直角边上都必须有点,也就是一组牛中的具有最小height的点和具有最小width的点。
直角三角形的边长也是固定的,cw = C/B,ch = C/A。这个还好说,从那个限制条件可以推出来的。初中都学过,呵呵。
Step1:求出经过一个点的所有可能存在的三角形。
其实也就是在该点下方的灰色区域中选择点来确定一个三角形。
Step2:求出经过一个点的所有可能存在的三角形中,最多包含的点数。
解法相当精妙。
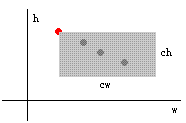
求一个三角形内的点数,可以分解为一个矩形内的点数减去一个梯形内的点数。
用这个方法,求出最上面那个三角形的点数之后。可以继续递推得到下面其他三角形的点数。
也就是加上一个矩形,再减去一个梯形。
如果点按照高度排序以后,那么后面矩形里的点一定是后出现的。这样就可以做到随时增加矩形。
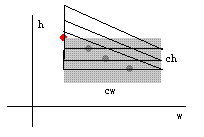
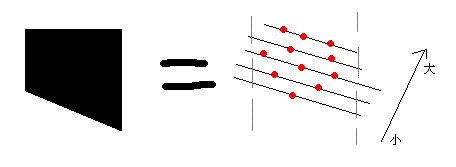
但是减去梯形这个操作,就难理解一点,把点按照A*H + B*W来排序,就能保证后面梯形里的点一定是后出现的。
可见,A*H + B*W 值的大小决定了他们的位置分布。完全可以保证这个顺序。
这种数形结合的方法实在是相当精妙!
在退出点的时候,我选择用优先队列来做。写得很锉

1 #include <cstdio> 2 #include <iostream> 3 #include <cstring> 4 #include <cctype> 5 #include <vector> 6 #include <queue> 7 #include <algorithm> 8 #define LL unsigned __int64 9 #pragma comment(linker, "/STACK:1024000000,1024000000") 10 using namespace std; 11 12 const int N=1010; 13 14 struct Node{ 15 int x,y; 16 int AH; 17 bool operator <(const Node &a) const { 18 if(y>a.y) return true; 19 else if(y==a.y){ 20 if(x<a.x) return true; 21 } 22 return false; 23 } 24 }node[N]; 25 int n,A,B,C,xh,yh; 26 struct Int_Node{ 27 int AH; 28 Int_Node(int x){AH=x;}; 29 bool operator<(const Int_Node &a)const { 30 if(AH<a.AH) return true; 31 return false; 32 } 33 }; 34 priority_queue<Int_Node>Q; 35 36 int main(){ 37 int ah,ans=0; 38 while(scanf("%d",&n)!=EOF){ 39 ans=0; 40 scanf("%d%d%d",&A,&B,&C); 41 yh=C/B; xh=C/A; 42 for(int i=0;i<n;i++){ 43 scanf("%d%d",&node[i].x,&node[i].y); 44 node[i].AH=A*node[i].x+B*node[i].y; 45 } 46 sort(node,node+n); 47 for(int i=0;i<n;i++){ 48 int xmin=node[i].x,ymin=node[i].y; 49 ah=A*xmin+B*ymin; 50 int j; 51 for(j=0;j<i;j++){ 52 if(node[j].y==ymin) break; 53 if(node[j].x<=xmin+xh&&node[j].y<=ymin+yh&&node[j].x>=xmin) 54 if(A*node[j].x+B*node[j].y-ah<=C) 55 Q.push(Int_Node(node[j].AH)); 56 } 57 for(j;j<n&&node[j].x<=xmin+xh&&node[j].y==ymin&&node[j].x>=xmin;j++) 58 Q.push(Int_Node(node[j].AH)); 59 int ts=Q.size(); 60 ans=max(ans,ts); 61 for(int k=j;node[k].y+yh>=node[i].y&&k<n;k++){ 62 if(node[k].y<ymin){ 63 ymin=node[k].y; 64 ah=A*xmin+B*ymin; 65 int p; 66 for(p=k;node[p].y==ymin&&p<n;p++){ 67 if(node[p].x<=xmin+xh&&node[p].x>=xmin){ 68 Q.push(Int_Node(node[p].AH)); 69 } 70 } 71 k=p-1;int tmp; 72 while(!Q.empty()){ 73 tmp=Q.top().AH; 74 if(tmp-ah>C){ 75 Q.pop(); 76 } 77 else 78 break; 79 } 80 ts=Q.size(); 81 ans=max(ans,ts); 82 } 83 } 84 while(!Q.empty()) 85 Q.pop(); 86 } 87 printf("%d\n",ans); 88 } 89 return 0; 90 }


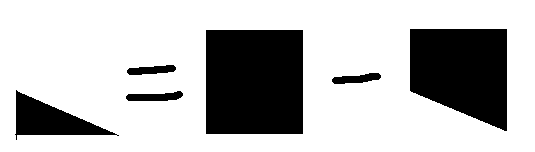
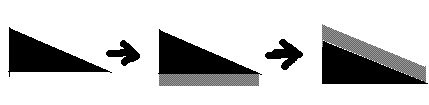


 浙公网安备 33010602011771号
浙公网安备 33010602011771号